沪科版七下数学第9章 分式单元测试卷(含答案)
文档属性
| 名称 | 沪科版七下数学第9章 分式单元测试卷(含答案) |
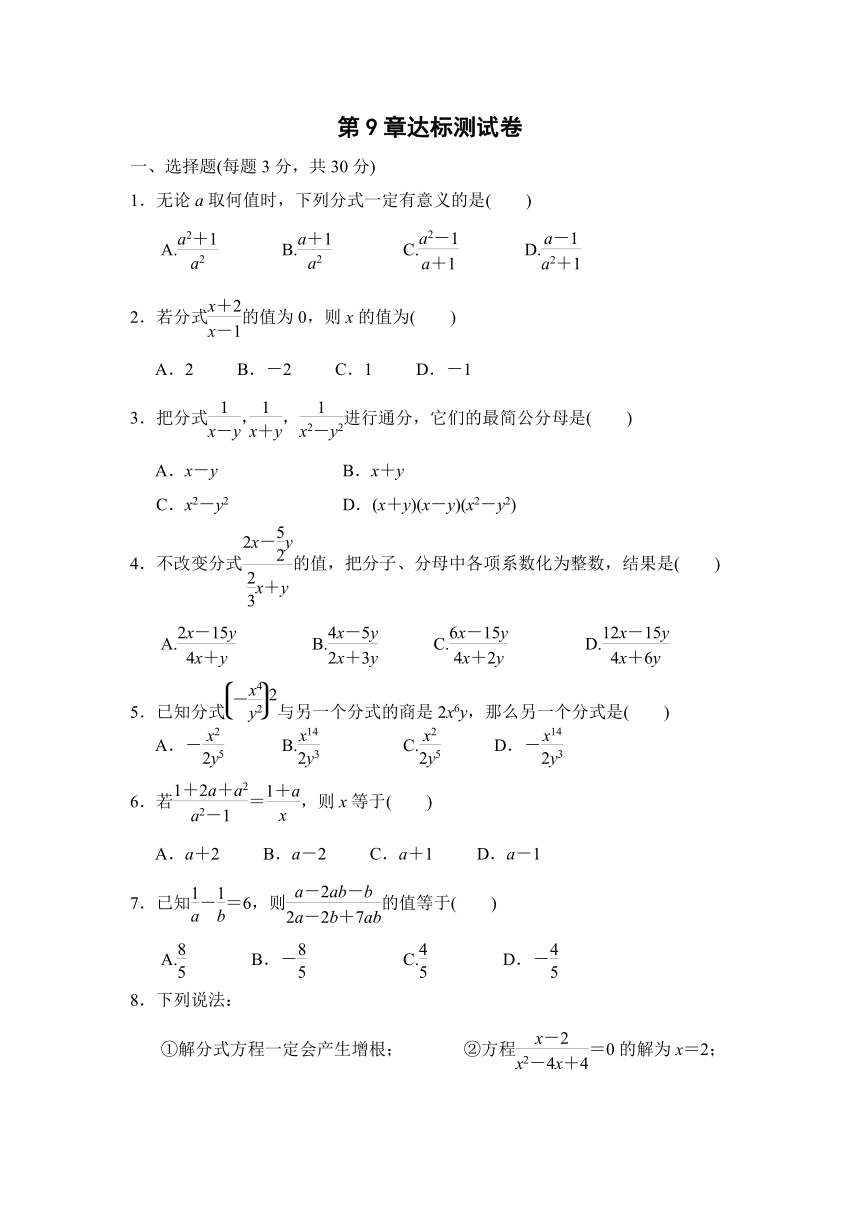
|
|
| 格式 | zip | ||
| 文件大小 | 85.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 13:24:39 | ||
图片预览
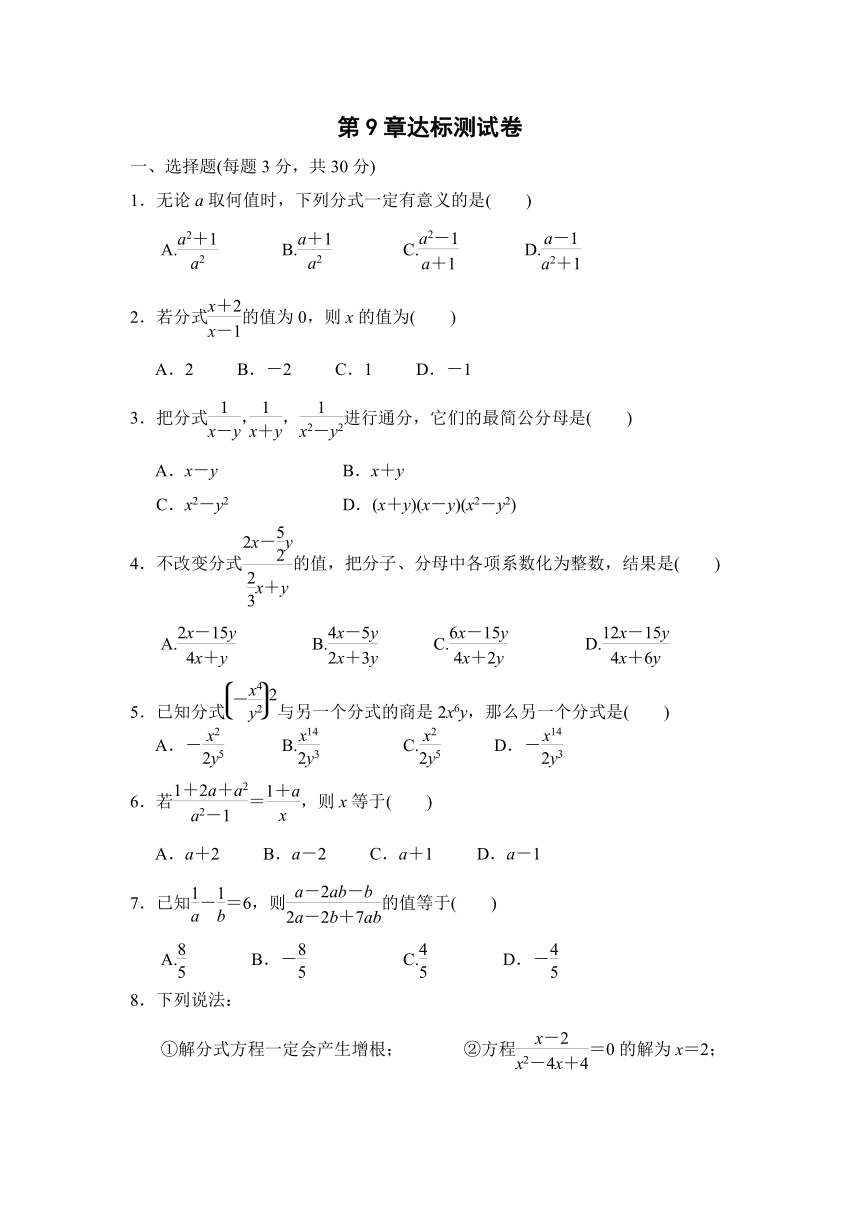



文档简介
第9章达标测试卷
一、选择题(每题3分,共30分)
1.无论a取何值时,下列分式一定有意义的是( )
A. B. C. D.
2.若分式的值为0,则x的值为( )
A.2 B.-2 C.1 D.-1
3.把分式,,进行通分,它们的最简公分母是( )
A.x-y B.x+y
C.x2-y2 D.(x+y)(x-y)(x2-y2)
4.不改变分式的值,把分子、分母中各项系数化为整数,结果是( )
A. B. C. D.
5.已知分式与另一个分式的商是2x6y,那么另一个分式是( )
A.- B. C. D.-
6.若=,则x等于( )
A.a+2 B.a-2 C.a+1 D.a-1
7.已知-=6,则的值等于( )
A. B.- C. D.-
8.下列说法:
①解分式方程一定会产生增根; ②方程=0的解为x=2;
③方程=的最简公分母是2x(2x-4);④=1+是分式方程.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.关于x的分式方程=1的解为正数,则字母a的取值范围为( )
A.a≥1且a≠2 B.a>1且a≠2
C.a≥1 D.a>1
10.现有甲、乙两种型号的机器人都被用来搬运某体育馆室内装潢材料,甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A.= B.= C.= D.=
二、填空题(每题3分,共12分)
11.化简÷的结果是________.
12. 已知x2-6x+9与|y-2|互为相反数,则式子÷(x+y)的值等于________.
13.请写出一个同时满足下列条件的分式:
(1)分式的值不可能为0;
(2)分式有意义时,x的取值范围是x≠±2;
(3)当x=0时,分式的值为-1.
你所写的分式为________________.
14.如果关于x的分式方程+=无解,那么a的值是________.
三、(每题6分,共12分)
15.计算:
(1)·÷; (2)÷.
16.在解决题目“已知x=2 020,求÷-+1的值”时,小明误将x=2 020看成了x=2 002,但算出的结果仍然正确,你能说说是为什么吗?
四、(每题6分,共12分)
17.解方程:
(1)-1=; (2)+=.
18.先化简,再求值:1-÷,其中x、y满足|x-2|+(2x-y-3)2=0.
五、(每题8分,共16分)
19.已知A=÷.
(1)化简A;
(2)当x是满足不等式组的整数时,求A的值.
20.观察:==-,==-,==-,==-,==-……
(1)请你猜想出表示上面式子的特点的一般规律,用含x(x表示整数)的等式表示出来,并验证;
(2)请利用上述规律,解方程++++=.
六、(12分)
21.某学校进行跳绳比赛,为此学校准备购买长、短两种跳绳若干条,若花费480元购买的长跳绳的数量是花费480元购买的短跳绳的数量的,已知每条长跳绳比每条短跳绳贵4元,求购买一条长跳绳、一条短跳绳分别需要多少元?
七、(12分)
22.甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合做2天就完成了全部工程,已知甲队单独完成工程所需的天数是乙队单独完成工程所需天数的.求甲、乙两队单独完成此项工程各需多少天?
八、(14分)
23.我们知道:分式和分数有着很多的相似点,如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子的次数小于分母的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式,
如:==+=1+;
==+=2+.
(1)下列分式中,属于真分式的是________(填序号);
① ② ③ ④
(2)将假分式化成整式与真分式的和的形式,若假分式的值为正整数,则整数a的值为多少?
(3)将假分式化成整式与真分式的和的形式.
答案
一、1.D 2.B 3.C 4.D 5.C 6.D 7.A 8.A 9.B 10.A
二、11. 12.
13.(答案不唯一)
14.6或-4
三、15.解:(1)原式=·=.
(2)原式=÷
=·=-.
16.解:原式=·-+1=-+1=1,与x的取值无关,所以不影响结果.
四、17.解:(1)方程两边同时乘以2(3x-1),得4-2(3x-1)=3.
解这个方程得x=.
检验:当x=时,2(3x-1)≠0.
所以x=是原方程的解.
(2)原方程可化为-=,
方程两边同时乘以(x+3)(x-3),得12-2(x+3)=x-3.
解这个方程得x=3.
检验:当x=3时,(x+3)(x-3)=0.
所以x=3是原方程的增根,
所以原方程无解.
18.解:原式=1-·=1-==-.
由|x-2|+(2x-y-3)2=0,得解得
则当x=2,y=1时,
原式=-=-.
五、19.解:(1)A=·=·=.
(2)
由①得x≥-1.
由②得x<3.
所以不等式组的解集为-1≤x<3,所以x=-1,0,1或2,
当x=-1,0,1时,A没有意义,
所以x=2.
当x=2时,A==.
20.解:(1)=-(x表示整数).
验证:右边=-=-===左边,
所以猜想正确.
(2)原方程可变形如下:
-+-+-+-+-=,
所以-=,
解得x=9.
经检验x=9是原方程的根,
所以原方程的根为x=9.
六、21.解:设购买一条长跳绳需要x元,则购买一条短跳绳需要(x-4)元,
根据题意得=×,
解得x=16,
经检验:x=16是原分式方程的根,
则x-4=12.
答:购买一条长跳绳、一条短跳绳分别需要16元、12元.
七、22.解:设乙队单独完成此项工程需x天,则甲队单独完成此项工程需x天.
依题意,得++=1,即++=1.
解这个方程得x=6.
经检验x=6是原方程的解,并符合题意.
此时,x=4.
答:乙队单独完成此项工程需6天,甲队单独完成此项工程需4天.
八、23.解:(1)③
(2)由题意可得,==2+,
若假分式的值为正整数,
则整数a满足2a-1=-5
或2a-1=1或2a-1=5.
解得a=-2或a=1或a=3.
(3)==+=a+1+.
一、选择题(每题3分,共30分)
1.无论a取何值时,下列分式一定有意义的是( )
A. B. C. D.
2.若分式的值为0,则x的值为( )
A.2 B.-2 C.1 D.-1
3.把分式,,进行通分,它们的最简公分母是( )
A.x-y B.x+y
C.x2-y2 D.(x+y)(x-y)(x2-y2)
4.不改变分式的值,把分子、分母中各项系数化为整数,结果是( )
A. B. C. D.
5.已知分式与另一个分式的商是2x6y,那么另一个分式是( )
A.- B. C. D.-
6.若=,则x等于( )
A.a+2 B.a-2 C.a+1 D.a-1
7.已知-=6,则的值等于( )
A. B.- C. D.-
8.下列说法:
①解分式方程一定会产生增根; ②方程=0的解为x=2;
③方程=的最简公分母是2x(2x-4);④=1+是分式方程.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.关于x的分式方程=1的解为正数,则字母a的取值范围为( )
A.a≥1且a≠2 B.a>1且a≠2
C.a≥1 D.a>1
10.现有甲、乙两种型号的机器人都被用来搬运某体育馆室内装潢材料,甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A.= B.= C.= D.=
二、填空题(每题3分,共12分)
11.化简÷的结果是________.
12. 已知x2-6x+9与|y-2|互为相反数,则式子÷(x+y)的值等于________.
13.请写出一个同时满足下列条件的分式:
(1)分式的值不可能为0;
(2)分式有意义时,x的取值范围是x≠±2;
(3)当x=0时,分式的值为-1.
你所写的分式为________________.
14.如果关于x的分式方程+=无解,那么a的值是________.
三、(每题6分,共12分)
15.计算:
(1)·÷; (2)÷.
16.在解决题目“已知x=2 020,求÷-+1的值”时,小明误将x=2 020看成了x=2 002,但算出的结果仍然正确,你能说说是为什么吗?
四、(每题6分,共12分)
17.解方程:
(1)-1=; (2)+=.
18.先化简,再求值:1-÷,其中x、y满足|x-2|+(2x-y-3)2=0.
五、(每题8分,共16分)
19.已知A=÷.
(1)化简A;
(2)当x是满足不等式组的整数时,求A的值.
20.观察:==-,==-,==-,==-,==-……
(1)请你猜想出表示上面式子的特点的一般规律,用含x(x表示整数)的等式表示出来,并验证;
(2)请利用上述规律,解方程++++=.
六、(12分)
21.某学校进行跳绳比赛,为此学校准备购买长、短两种跳绳若干条,若花费480元购买的长跳绳的数量是花费480元购买的短跳绳的数量的,已知每条长跳绳比每条短跳绳贵4元,求购买一条长跳绳、一条短跳绳分别需要多少元?
七、(12分)
22.甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合做2天就完成了全部工程,已知甲队单独完成工程所需的天数是乙队单独完成工程所需天数的.求甲、乙两队单独完成此项工程各需多少天?
八、(14分)
23.我们知道:分式和分数有着很多的相似点,如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子的次数小于分母的次数的分式称为真分式;反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式,
如:==+=1+;
==+=2+.
(1)下列分式中,属于真分式的是________(填序号);
① ② ③ ④
(2)将假分式化成整式与真分式的和的形式,若假分式的值为正整数,则整数a的值为多少?
(3)将假分式化成整式与真分式的和的形式.
答案
一、1.D 2.B 3.C 4.D 5.C 6.D 7.A 8.A 9.B 10.A
二、11. 12.
13.(答案不唯一)
14.6或-4
三、15.解:(1)原式=·=.
(2)原式=÷
=·=-.
16.解:原式=·-+1=-+1=1,与x的取值无关,所以不影响结果.
四、17.解:(1)方程两边同时乘以2(3x-1),得4-2(3x-1)=3.
解这个方程得x=.
检验:当x=时,2(3x-1)≠0.
所以x=是原方程的解.
(2)原方程可化为-=,
方程两边同时乘以(x+3)(x-3),得12-2(x+3)=x-3.
解这个方程得x=3.
检验:当x=3时,(x+3)(x-3)=0.
所以x=3是原方程的增根,
所以原方程无解.
18.解:原式=1-·=1-==-.
由|x-2|+(2x-y-3)2=0,得解得
则当x=2,y=1时,
原式=-=-.
五、19.解:(1)A=·=·=.
(2)
由①得x≥-1.
由②得x<3.
所以不等式组的解集为-1≤x<3,所以x=-1,0,1或2,
当x=-1,0,1时,A没有意义,
所以x=2.
当x=2时,A==.
20.解:(1)=-(x表示整数).
验证:右边=-=-===左边,
所以猜想正确.
(2)原方程可变形如下:
-+-+-+-+-=,
所以-=,
解得x=9.
经检验x=9是原方程的根,
所以原方程的根为x=9.
六、21.解:设购买一条长跳绳需要x元,则购买一条短跳绳需要(x-4)元,
根据题意得=×,
解得x=16,
经检验:x=16是原分式方程的根,
则x-4=12.
答:购买一条长跳绳、一条短跳绳分别需要16元、12元.
七、22.解:设乙队单独完成此项工程需x天,则甲队单独完成此项工程需x天.
依题意,得++=1,即++=1.
解这个方程得x=6.
经检验x=6是原方程的解,并符合题意.
此时,x=4.
答:乙队单独完成此项工程需6天,甲队单独完成此项工程需4天.
八、23.解:(1)③
(2)由题意可得,==2+,
若假分式的值为正整数,
则整数a满足2a-1=-5
或2a-1=1或2a-1=5.
解得a=-2或a=1或a=3.
(3)==+=a+1+.
