2020春湘教版九下数学第1章二次函数1.4二次函数与一元二次方程的联系教学课件(17张PPT)
文档属性
| 名称 | 2020春湘教版九下数学第1章二次函数1.4二次函数与一元二次方程的联系教学课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览






文档简介
课件17张PPT。教学课件
数学 九年级下册 湘教版
第1章 二次函数
1.4 二次函数与一元二次方程的联系1、 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。
方程根的情况是:当△﹥0 时方程 ;
当△=0时,方程 ;
当△﹤0时,方程 。2.抛物线y=x2+2x-4的对称轴是______, 开口方向_____,顶点坐标是________.3.已知抛物线与x轴交于A(-1,0)和B(1,0),并经
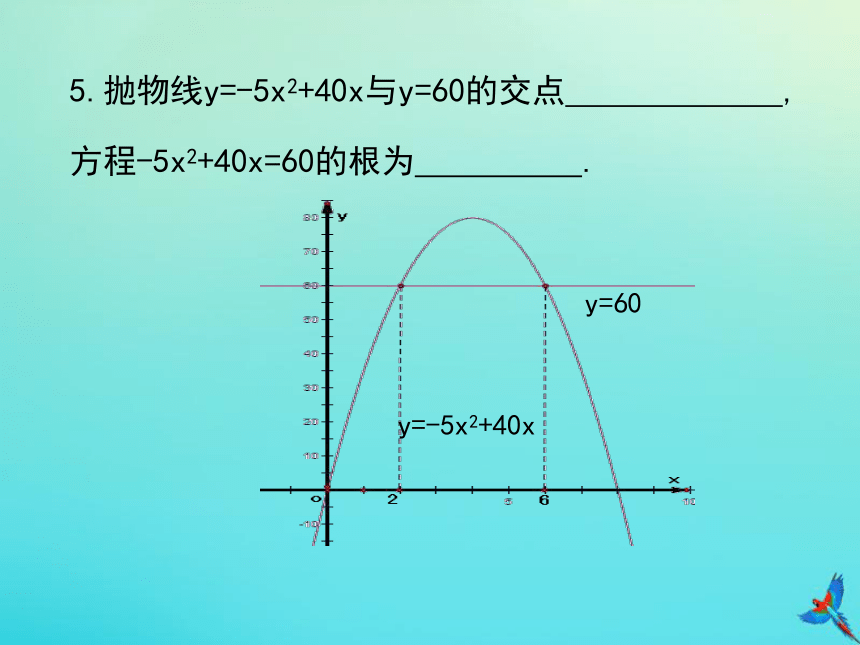
过点M(0,1),则此抛物线的解析式为__________.4.抛物线y=2(x-2)(x-3)与x轴的交点为___________,与y轴的交点为______,方程2(x-2)(x-3)=0的根为 ____ .5.抛物线y=-5x2+40x与y=60的交点 ,
方程-5x2+40x=60的根为 . 已知函数值y=0,求对应自变量x.请问这位同学的跳远成绩是多少? 高度y(m)与水平距离x(m)之间具有的关系: 高度h(m)与时间t(s)之间具有的关系: h=20t-5t2 球从飞出到落地需要多少时间? 已知函数值h=0,求对应自变量t. 已知二次函数 y=ax2 +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax2 +bx+c=0 (a≠0).(1)球的飞行高度能否达到15m? 若能,需要多少飞行时间? 已知函数值h=15,求对应自变量t.(2)球的飞行高度能否达到20m? 若能,需要多少飞行时间?(3)球的飞行高度能否达到20.5m? 若能,需要多少飞行时间? 已知二次函数 y=ax2 +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax2 +bx+c=m(或ax2 +bx+c-m=0) (a≠0).h=20t-5t2以上关系反之也成立. 根据图象你能得出相应方程的解吗? (3)方程x2 -x+1=0的根是______________. 如果抛物线 y=ax2 +bx+c(a≠0)与x轴有公共点(x0 ,0),那么x=x0 就是方程 ax2+bx+c=0的一个根.x1 =-2, x2 =1x1 =x2 =3无实数根有两个交点有两个相异的实数根有一个交点有两个相等的实数根没有交点没有实数根b2-4ac > 0b2-4ac = 0b2-4ac < 0说明:a≠0下列二次函数的图象与x轴有交点吗?有几个交点? (5) y=2x2 - (4k+1)x+2k2 -1; (1) y=2x2 +x-3; (2) y=-4x2 -4x-1; (3) y=3x2 -2x+3; (4) y=x2 +(2k+1)x-k2 +k;若此抛物线与x轴有两个交点,求k的取值范围.基础练习:1.不与x轴相交的抛物线是( )
A y= 2x2 – 3 B y= - 2x2 + 3
C y= - x2 –3x D y= - 2(x+1)2 - 32.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定DC3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有__个交点 .4.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=___.11165.若函数y=-x2+2kx+2与坐标轴交点的个数有 个.3(1,0)6.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c =0根的情况是( )
A 有两个不相等的实数根
B 有两个异号的实数根
C有两个相等的实数根
D 没有实数根
D-3例: 利用函数图象求方程 x 2 -2x-2=0的实数根
(精确到0.1)解: 作y=x2 -2x-2的图象(如图),它与x轴的公共点
的横坐标大约是 – 0.7 , 2.7
所以方程x 2 -2x-2=0的实数根为
x? ≈-0.7, x? ≈2.7.练习:根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3 C 3.24 0b2-4ac = 0b2-4ac < 02. 二次函数与一元二次方程的关系
y=ax2+bx+cax2+bx+c=ky取定值k方程的根交点的横坐标与直线y=k1.二次函数y=ax2+bx+c与X轴交点个数的确定3.用交点式求二次函数表达式y=a(x-x1)(x-x2)数形结合的思想
数学 九年级下册 湘教版
第1章 二次函数
1.4 二次函数与一元二次方程的联系1、 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。
方程根的情况是:当△﹥0 时方程 ;
当△=0时,方程 ;
当△﹤0时,方程 。2.抛物线y=x2+2x-4的对称轴是______, 开口方向_____,顶点坐标是________.3.已知抛物线与x轴交于A(-1,0)和B(1,0),并经
过点M(0,1),则此抛物线的解析式为__________.4.抛物线y=2(x-2)(x-3)与x轴的交点为___________,与y轴的交点为______,方程2(x-2)(x-3)=0的根为 ____ .5.抛物线y=-5x2+40x与y=60的交点 ,
方程-5x2+40x=60的根为 . 已知函数值y=0,求对应自变量x.请问这位同学的跳远成绩是多少? 高度y(m)与水平距离x(m)之间具有的关系: 高度h(m)与时间t(s)之间具有的关系: h=20t-5t2 球从飞出到落地需要多少时间? 已知函数值h=0,求对应自变量t. 已知二次函数 y=ax2 +bx+c (a≠0)的函数值为0,求自变量x的值,可以看作解一元二次方程 ax2 +bx+c=0 (a≠0).(1)球的飞行高度能否达到15m? 若能,需要多少飞行时间? 已知函数值h=15,求对应自变量t.(2)球的飞行高度能否达到20m? 若能,需要多少飞行时间?(3)球的飞行高度能否达到20.5m? 若能,需要多少飞行时间? 已知二次函数 y=ax2 +bx+c (a≠0)的函数值为m,求自变量x的值,可以看作解一元二次方程 ax2 +bx+c=m(或ax2 +bx+c-m=0) (a≠0).h=20t-5t2以上关系反之也成立. 根据图象你能得出相应方程的解吗? (3)方程x2 -x+1=0的根是______________. 如果抛物线 y=ax2 +bx+c(a≠0)与x轴有公共点(x0 ,0),那么x=x0 就是方程 ax2+bx+c=0的一个根.x1 =-2, x2 =1x1 =x2 =3无实数根有两个交点有两个相异的实数根有一个交点有两个相等的实数根没有交点没有实数根b2-4ac > 0b2-4ac = 0b2-4ac < 0说明:a≠0下列二次函数的图象与x轴有交点吗?有几个交点? (5) y=2x2 - (4k+1)x+2k2 -1; (1) y=2x2 +x-3; (2) y=-4x2 -4x-1; (3) y=3x2 -2x+3; (4) y=x2 +(2k+1)x-k2 +k;若此抛物线与x轴有两个交点,求k的取值范围.基础练习:1.不与x轴相交的抛物线是( )
A y= 2x2 – 3 B y= - 2x2 + 3
C y= - x2 –3x D y= - 2(x+1)2 - 32.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定DC3.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=____,此时抛物线 y=x2-2x+m与x轴有__个交点 .4.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=___.11165.若函数y=-x2+2kx+2与坐标轴交点的个数有 个.3(1,0)6.已知抛物线y=ax2+bx+c的图象如图,则关于x的方程ax2+bx+c =0根的情况是( )
A 有两个不相等的实数根
B 有两个异号的实数根
C有两个相等的实数根
D 没有实数根
D-3例: 利用函数图象求方程 x 2 -2x-2=0的实数根
(精确到0.1)解: 作y=x2 -2x-2的图象(如图),它与x轴的公共点
的横坐标大约是 – 0.7 , 2.7
所以方程x 2 -2x-2=0的实数根为
x? ≈-0.7, x? ≈2.7.练习:根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A 3
y=ax2+bx+cax2+bx+c=ky取定值k方程的根交点的横坐标与直线y=k1.二次函数y=ax2+bx+c与X轴交点个数的确定3.用交点式求二次函数表达式y=a(x-x1)(x-x2)数形结合的思想
