六年级下册数学课件-圆柱的体积-人教版(共22张PPT)
文档属性
| 名称 | 六年级下册数学课件-圆柱的体积-人教版(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 14:24:59 | ||
图片预览



文档简介
(共22张PPT)
圆柱的体积
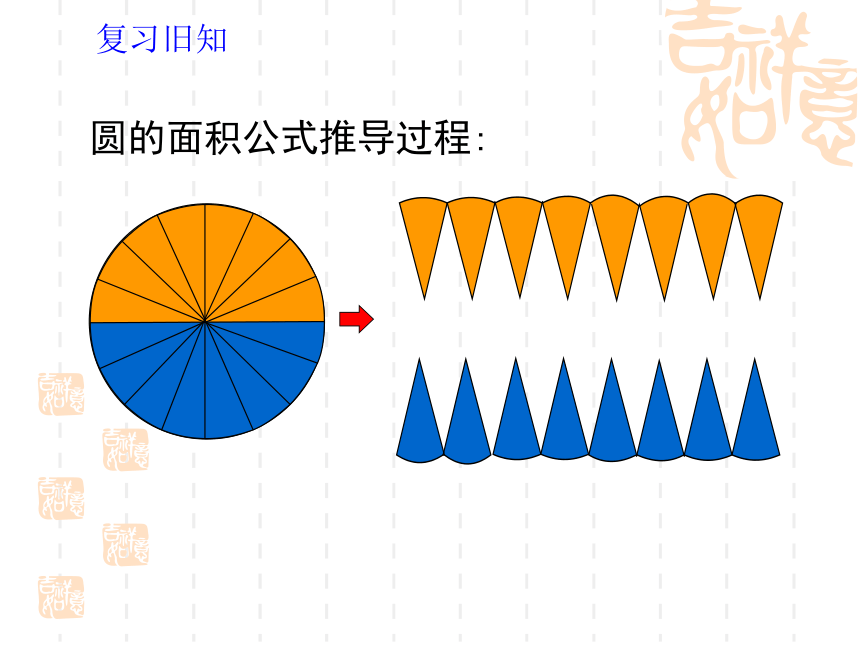
圆的面积公式推导过程:
复习旧知
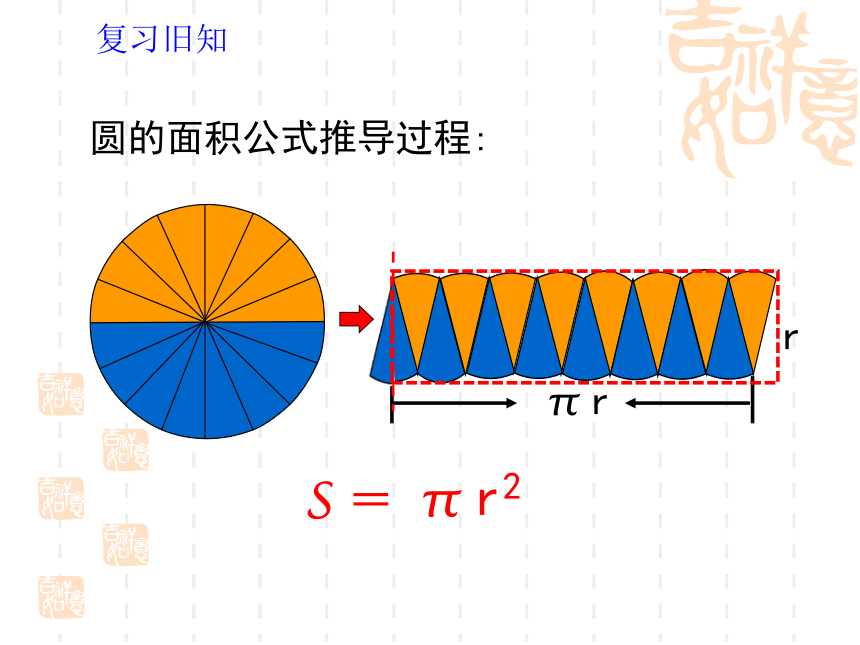
π r
r
S = π r2
复习旧知
圆的面积公式推导过程:
自学提纲:
(1)自学课本25页例5,了解圆柱体体积公式的推导过程。
(2)动手操作:(以小组为单位)
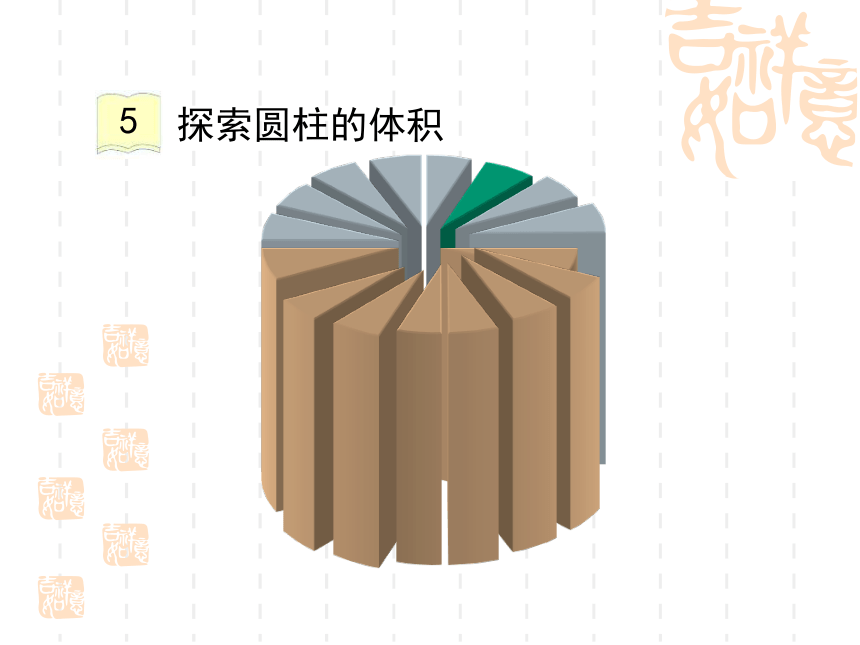
要求:圆柱体能转化成我们学过的什么立体图形?你是怎样转化成这个立体图形的?将组内的教具和学具切一切,拼一拼,然后组内交流。
(3)这个长方体与圆柱体比较一下,什么变了?什么没变?
(4)转化以后的立体图形和圆柱体之间有什么关系?
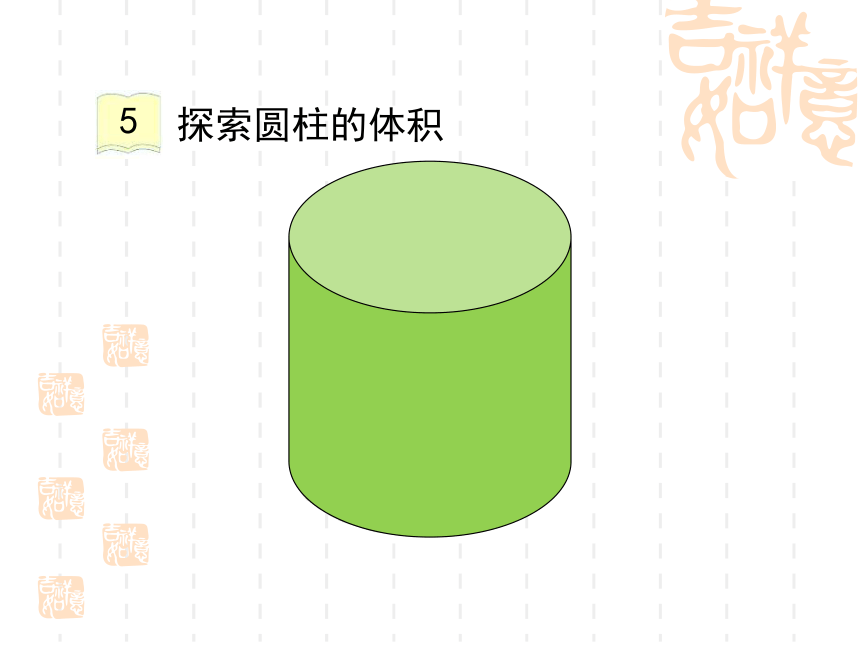
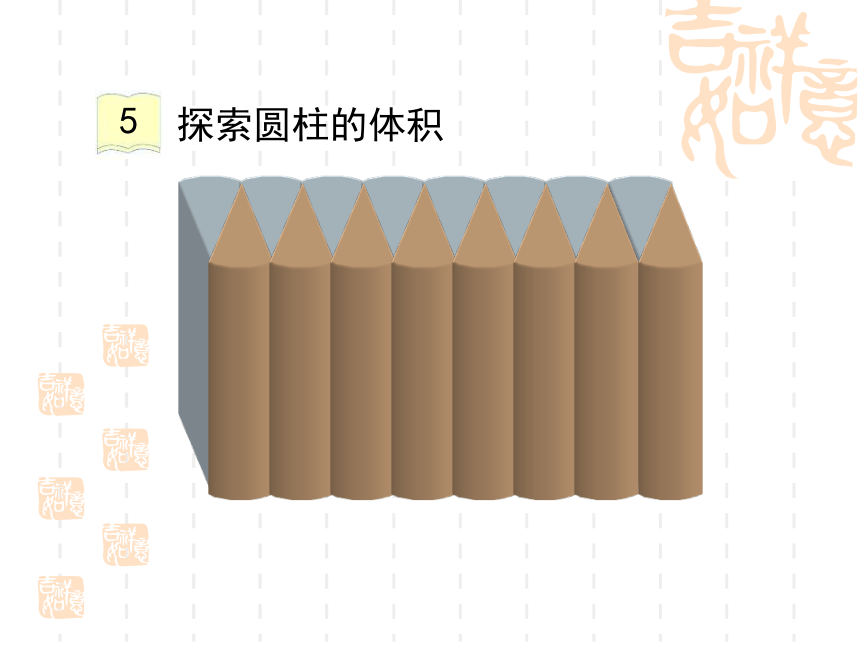
探索圆柱的体积
探索圆柱的体积
探索圆柱的体积
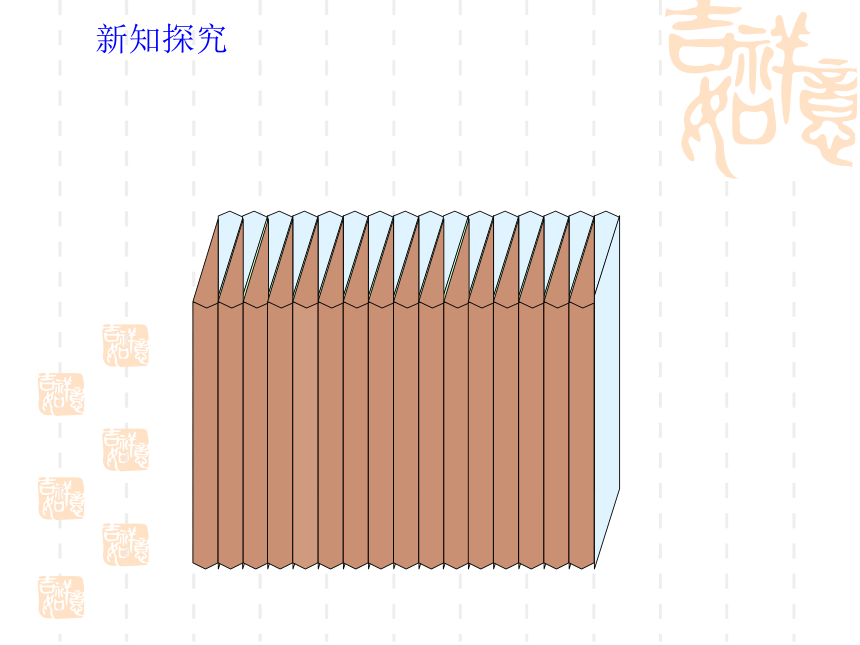
新知探究
通过老师的切拼,你发现了什么?
长方体的体积
底面积
高
=
×
=
×
新知探究
圆柱的体积=底面积×高
V圆柱=S底面积×h
21
22.4
自学提纲(二)
根据圆柱体积的计算公式,如果要求圆柱的体积,你还知道哪些条件就可以求?
2.求下面各圆柱体的体积(单位:cm)
智
慧
屋
已知一个圆柱的侧面积37.68平方厘米,底面半径为3厘米,求这个圆柱的体积。
(1)你会计算它们的体积吗?
(2)试写出它们的体积公式。
拓展延伸
h = h
自学提纲(二)
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
甲 乙
图1:
新知探究
h = h
甲 乙
图1:
新知探究
高相等时,底面积越大的体积越大。
新知探究
图2:
将一个圆柱截成不相等的两段,哪个圆柱体积大?
底面积相等时,高越长的体积越大。
圆柱体积的大小与哪些条件有关?
新知探究
底面积
已知:
S,h 直求V;
r,h 先求S,再求V;
d,h 先求r,再求S,
然后求V
小结与作业
本节课你有哪些收获?
作业:
课本第25页“做一做”第1题、第2题。
圆柱的体积
圆的面积公式推导过程:
复习旧知
π r
r
S = π r2
复习旧知
圆的面积公式推导过程:
自学提纲:
(1)自学课本25页例5,了解圆柱体体积公式的推导过程。
(2)动手操作:(以小组为单位)
要求:圆柱体能转化成我们学过的什么立体图形?你是怎样转化成这个立体图形的?将组内的教具和学具切一切,拼一拼,然后组内交流。
(3)这个长方体与圆柱体比较一下,什么变了?什么没变?
(4)转化以后的立体图形和圆柱体之间有什么关系?
探索圆柱的体积
探索圆柱的体积
探索圆柱的体积
新知探究
通过老师的切拼,你发现了什么?
长方体的体积
底面积
高
=
×
=
×
新知探究
圆柱的体积=底面积×高
V圆柱=S底面积×h
21
22.4
自学提纲(二)
根据圆柱体积的计算公式,如果要求圆柱的体积,你还知道哪些条件就可以求?
2.求下面各圆柱体的体积(单位:cm)
智
慧
屋
已知一个圆柱的侧面积37.68平方厘米,底面半径为3厘米,求这个圆柱的体积。
(1)你会计算它们的体积吗?
(2)试写出它们的体积公式。
拓展延伸
h = h
自学提纲(二)
1、甲圆柱与乙圆柱谁的体积大?
2、它们的什么条件是相同的?
3、圆柱的体积大小与什么有关?
甲 乙
图1:
新知探究
h = h
甲 乙
图1:
新知探究
高相等时,底面积越大的体积越大。
新知探究
图2:
将一个圆柱截成不相等的两段,哪个圆柱体积大?
底面积相等时,高越长的体积越大。
圆柱体积的大小与哪些条件有关?
新知探究
底面积
已知:
S,h 直求V;
r,h 先求S,再求V;
d,h 先求r,再求S,
然后求V
小结与作业
本节课你有哪些收获?
作业:
课本第25页“做一做”第1题、第2题。
