2020湘教版八下数学第2章四边形2.1多边形第1课时习题课件(20张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.1多边形第1课时习题课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 585.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 21:10:11 | ||
图片预览








文档简介
课件20张PPT。第2章 四 边 形
2.1 多 边 形?
第1课时1.了解多边形及正多边形的相关概念.(重点)
2.理解多边形内角和公式的探索过程,并掌握多边形的内角和公式.(难点)
3.能利用多边形内角和公式解决简单的计算问题.(难点)一、多边形的有关概念
1.在平面内,由若干条不在同一条直线上的线段_________相连
组成的_____图形叫作多边形.
2.在多边形中,连结_______________的线段叫作多边形的对角
线.
3.在平面内,内角都_____、边也都_____的多边形叫作正多边
形.首尾顺次封闭不相邻两个顶点相等相等二、多边形的内角和
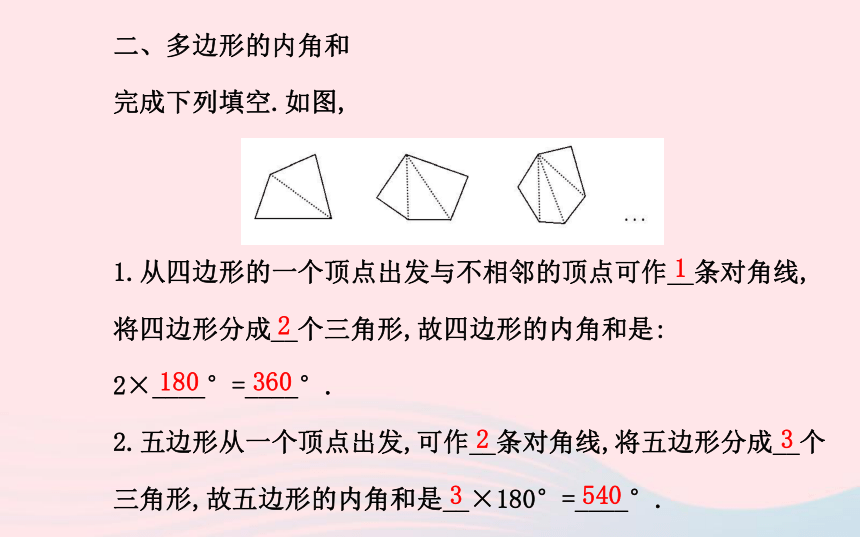
完成下列填空.如图,
1.从四边形的一个顶点出发与不相邻的顶点可作__条对角线,
将四边形分成__个三角形,故四边形的内角和是:
2×____°=____°.
2.五边形从一个顶点出发,可作__条对角线,将五边形分成__个
三角形,故五边形的内角和是__×180°=____°.12180360233540【思考】(1)从n(n≥3)边形的一个顶点出发,将n边形分成多少个三角形?
提示:(n-2)个.
(2)n(n≥3)边形的内角和与其边数n的关系是什么?
提示:内角和为(n-2)×180°.【总结】(1)n边形的内角和等于_____________,其中n≥3,且
为自然数.
(2)多边形的内角和与它的_____有关.(n-2)·180°边数 (打“√”或“×”)
(1)三角形不是多边形. ( )
(2)一个正多边形的每个内角是120°,它是正六边形. ( )
(3)多边形的边数每增加1,其内角和增加180°. ( )
(4)所有内角相等的多边形是正多边形. ( )×√√×知识点 多边形内角和公式的应用?
【例】已知两个多边形的所有内角的和为1800°,且两多边形
的边数之比为2∶5,求这两个多边形的边数.
【解题探究】
(1)因为两个多边形的边数之比为2∶5,所以设这两个多边形的
边数分别是2x和___.
(2)由多边形内角和定理可得两个多边形的内角和分别是多少?
提示:(2x-2)·180°和(5x-2)·180°.5x(3)由两个多边形的所有内角的和为1800°可列方程为什么?
提示:(2x-2)·180°+(5x-2)·180°=1800°.
(4)解方程得x=__,所以2x=__,5x=___,
所以这两个多边形的边数分别为__和___.2410410【总结提升】多边形的内角和的两点注意
1.一个多边形的内角和取决于它的边数,随着边数的增加而增
加,并且每增加一条边,内角和就增加180°.
2.因为正多边形的每个内角都相等,所以正多边形的每个内角
的度数可以确定,它是题组:多边形内角和公式的应用
1.四边形的内角和的度数为 ( )
A.180° B.270° C.360° D.540°
【解析】选C.(4-2)·180°=360°.2.正八边形的每个内角为 ( )
A.120° B.135° C.140° D.144°
【解析】选B.[(n-2)×180°]÷n=[(8-2)×180°]÷8=135°.3.已知一个多边形的内角和是540°,则这个
多边形是 ( )
A.四边形 B.五边形
C.六边形 D.七边形
【解析】选B.设这个多边形是n边形,根据题意有(n-2)×180°
=540°,解得n=5.4.已知一个多边形的内角和是1080°,这个多边形的边数是 .
【解析】设边数为n,所以有(n-2)×180°=1080°,解得n=8.
答案:85.如图,人民币旧版壹角硬币内部的正多边形
每个内角度数是 .
【解析】因为九边形的内角和为(9-2)·180°=1260°,又因为
九边形的每个内角都相等,所以每个内角的度数为1260°÷9
=140°.
答案:140°6.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.【解析】如图所示,
因为∠1=∠2,∠3=∠4,∠5=∠6,
所以∠A+∠B=∠4+∠6,
∠C+∠D=∠2+∠6,
∠E+∠F=∠2+∠4,所以∠A+∠B+∠C+∠D+∠E+∠F
=∠4+∠6+∠2+∠6+∠2+∠4
=2(∠2+∠4+∠6).
又因为∠2+∠4+∠6=180°,
所以∠A+∠B+∠C+∠D+∠E+∠F
=2×180°=360°.7.已知:如图,在五边形ABCDE中,AB∥CD,求图形中的x的值.
【解析】因为AB∥CD,∠C=60°,
所以∠B=180°-60°=120°,
所以(5-2)×180°=x+150°+125°+60°+120°,
所以x=85°.【想一想错在哪?】计算十边形的内角和的度数.
提示:多边形内角和公式记忆错误.
2.1 多 边 形?
第1课时1.了解多边形及正多边形的相关概念.(重点)
2.理解多边形内角和公式的探索过程,并掌握多边形的内角和公式.(难点)
3.能利用多边形内角和公式解决简单的计算问题.(难点)一、多边形的有关概念
1.在平面内,由若干条不在同一条直线上的线段_________相连
组成的_____图形叫作多边形.
2.在多边形中,连结_______________的线段叫作多边形的对角
线.
3.在平面内,内角都_____、边也都_____的多边形叫作正多边
形.首尾顺次封闭不相邻两个顶点相等相等二、多边形的内角和
完成下列填空.如图,
1.从四边形的一个顶点出发与不相邻的顶点可作__条对角线,
将四边形分成__个三角形,故四边形的内角和是:
2×____°=____°.
2.五边形从一个顶点出发,可作__条对角线,将五边形分成__个
三角形,故五边形的内角和是__×180°=____°.12180360233540【思考】(1)从n(n≥3)边形的一个顶点出发,将n边形分成多少个三角形?
提示:(n-2)个.
(2)n(n≥3)边形的内角和与其边数n的关系是什么?
提示:内角和为(n-2)×180°.【总结】(1)n边形的内角和等于_____________,其中n≥3,且
为自然数.
(2)多边形的内角和与它的_____有关.(n-2)·180°边数 (打“√”或“×”)
(1)三角形不是多边形. ( )
(2)一个正多边形的每个内角是120°,它是正六边形. ( )
(3)多边形的边数每增加1,其内角和增加180°. ( )
(4)所有内角相等的多边形是正多边形. ( )×√√×知识点 多边形内角和公式的应用?
【例】已知两个多边形的所有内角的和为1800°,且两多边形
的边数之比为2∶5,求这两个多边形的边数.
【解题探究】
(1)因为两个多边形的边数之比为2∶5,所以设这两个多边形的
边数分别是2x和___.
(2)由多边形内角和定理可得两个多边形的内角和分别是多少?
提示:(2x-2)·180°和(5x-2)·180°.5x(3)由两个多边形的所有内角的和为1800°可列方程为什么?
提示:(2x-2)·180°+(5x-2)·180°=1800°.
(4)解方程得x=__,所以2x=__,5x=___,
所以这两个多边形的边数分别为__和___.2410410【总结提升】多边形的内角和的两点注意
1.一个多边形的内角和取决于它的边数,随着边数的增加而增
加,并且每增加一条边,内角和就增加180°.
2.因为正多边形的每个内角都相等,所以正多边形的每个内角
的度数可以确定,它是题组:多边形内角和公式的应用
1.四边形的内角和的度数为 ( )
A.180° B.270° C.360° D.540°
【解析】选C.(4-2)·180°=360°.2.正八边形的每个内角为 ( )
A.120° B.135° C.140° D.144°
【解析】选B.[(n-2)×180°]÷n=[(8-2)×180°]÷8=135°.3.已知一个多边形的内角和是540°,则这个
多边形是 ( )
A.四边形 B.五边形
C.六边形 D.七边形
【解析】选B.设这个多边形是n边形,根据题意有(n-2)×180°
=540°,解得n=5.4.已知一个多边形的内角和是1080°,这个多边形的边数是 .
【解析】设边数为n,所以有(n-2)×180°=1080°,解得n=8.
答案:85.如图,人民币旧版壹角硬币内部的正多边形
每个内角度数是 .
【解析】因为九边形的内角和为(9-2)·180°=1260°,又因为
九边形的每个内角都相等,所以每个内角的度数为1260°÷9
=140°.
答案:140°6.如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.【解析】如图所示,
因为∠1=∠2,∠3=∠4,∠5=∠6,
所以∠A+∠B=∠4+∠6,
∠C+∠D=∠2+∠6,
∠E+∠F=∠2+∠4,所以∠A+∠B+∠C+∠D+∠E+∠F
=∠4+∠6+∠2+∠6+∠2+∠4
=2(∠2+∠4+∠6).
又因为∠2+∠4+∠6=180°,
所以∠A+∠B+∠C+∠D+∠E+∠F
=2×180°=360°.7.已知:如图,在五边形ABCDE中,AB∥CD,求图形中的x的值.
【解析】因为AB∥CD,∠C=60°,
所以∠B=180°-60°=120°,
所以(5-2)×180°=x+150°+125°+60°+120°,
所以x=85°.【想一想错在哪?】计算十边形的内角和的度数.
提示:多边形内角和公式记忆错误.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
