2020湘教版八下数学第2章四边形2.2.1平行四边形的性质第1课时习题课件(31张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.2.1平行四边形的性质第1课时习题课件(31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 755.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 21:12:21 | ||
图片预览







文档简介
课件31张PPT。2.2 平行四边形?
2.2.1 平行四边形的性质(第1课时)1.理解平行四边形的概念和性质.(重点)
2.理解两条平行线间的距离.(重点)
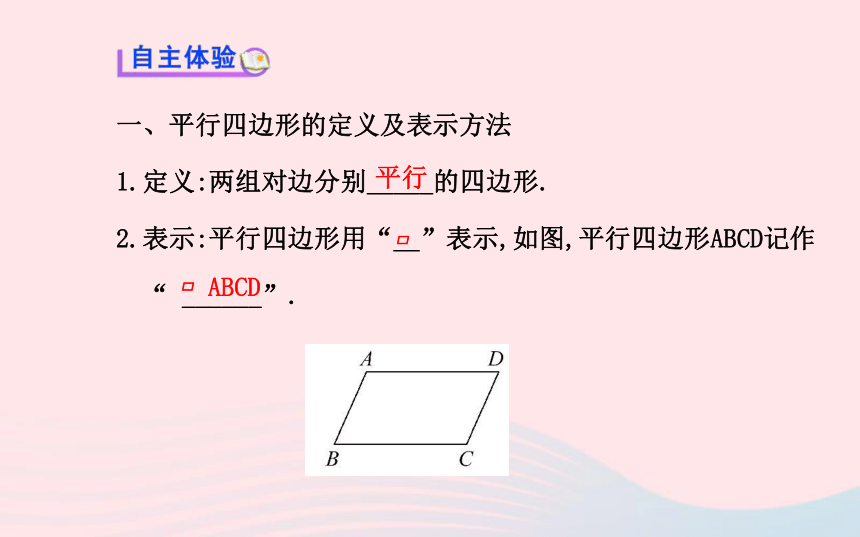
3.会用平行四边形的性质进行计算或证明.(重点、难点)一、平行四边形的定义及表示方法
1.定义:两组对边分别_____的四边形.
2.表示:平行四边形用“__”表示,如图,平行四边形ABCD记作
“ ______”.平行??ABCD二、平行四边形的性质
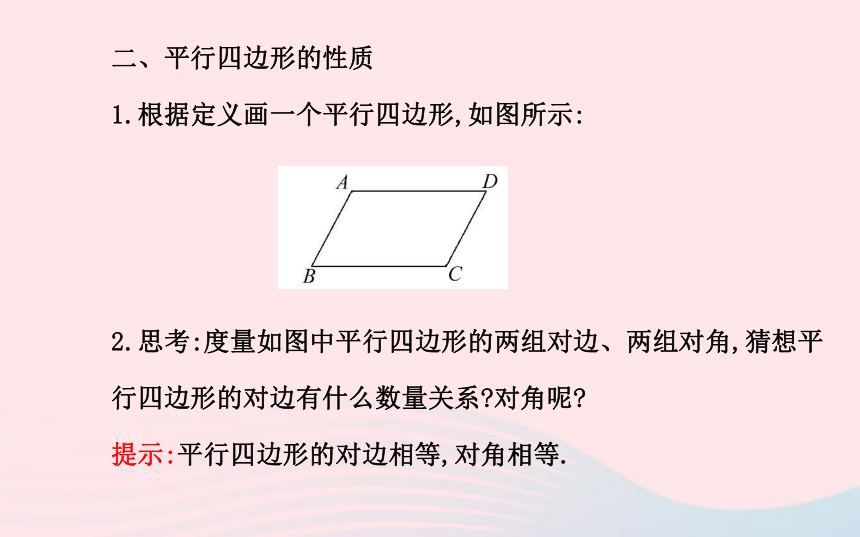
1.根据定义画一个平行四边形,如图所示:
2.思考:度量如图中平行四边形的两组对边、两组对角,猜想平行四边形的对边有什么数量关系?对角呢?
提示:平行四边形的对边相等,对角相等.3.证明猜想:
(1)证明线段、角相等的一般方法是利用三角形全等,怎样构造
三角形?
提示:连接AC.
(2)由平行四边形的定义及AC是公共边,易得△ABC___△CDA.
(3)由此可得到哪些相等的线段、角?
提示:AD=CB,AB=CD,∠B=∠D,∠BAD=∠DCB.≌【总结】平行四边形的性质:平行四边形的对边_____;平行四
边形的对角_____.相等相等三、两条平行线之间的距离
两条平行线中,一条直线上_________到另一条直线的距离.任意一点 (打“√”或“×”)
(1)平行四边形的邻边相等. ( )
(2)平行四边形的邻角相等. ( )
(3)一组对边平行的四边形是平行四边形. ( )
(4)夹在两条平行线间的平行线段相等. ( ) ×××√知识点 1 平行四边形的性质定理?
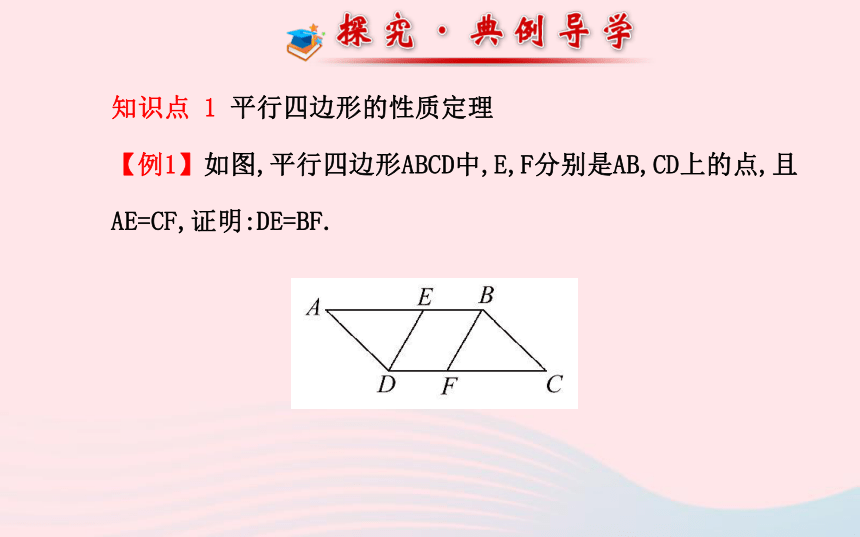
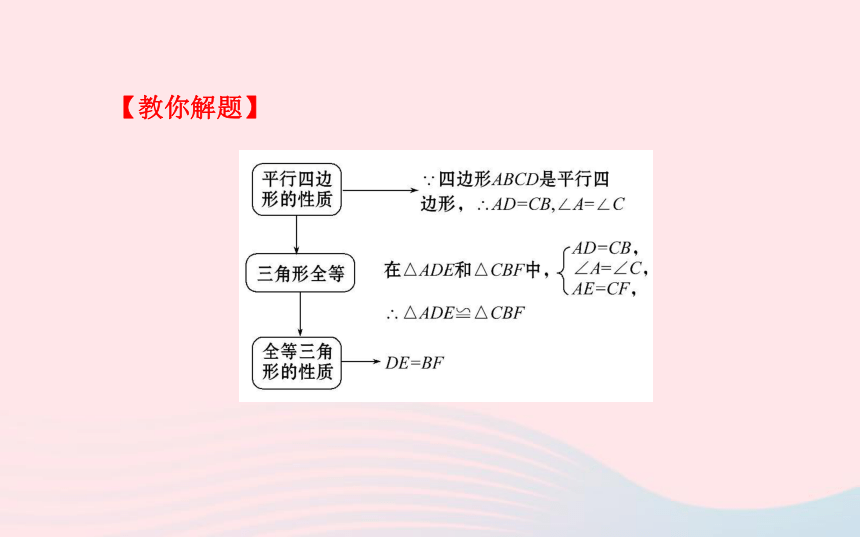
【例1】如图,平行四边形ABCD中,E,F分别是AB,CD上的点,且AE=CF,证明:DE=BF.【教你解题】【总结提升】平行四边形的性质定理的应用
1.利用平行四边形的性质是证明线段(或角)相等的一种常用方法.应用时注意挖掘隐含条件:平行四边形的对边平行且相等;对角相等、邻角互补.
2.常常结合全等三角形、平行线的性质等知识进行综合考查.知识点 2 平行四边形的边、角性质的应用?
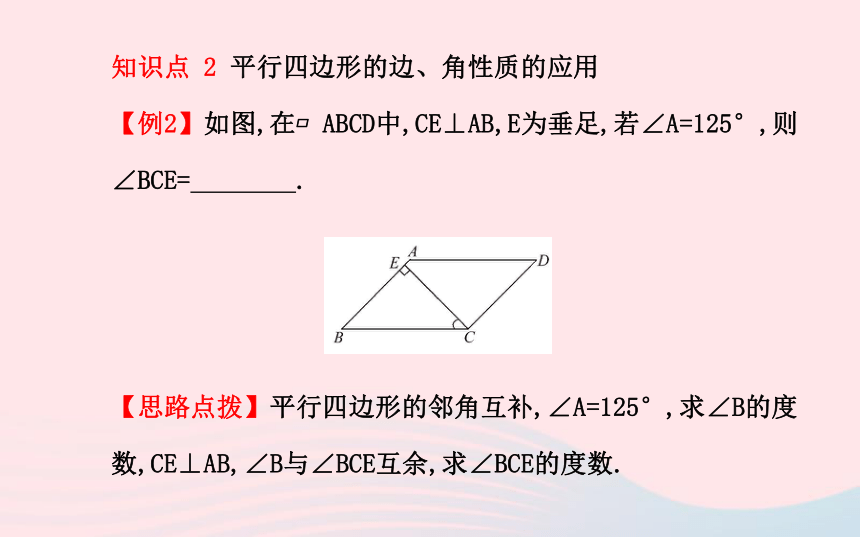
【例2】如图,在?ABCD中,CE⊥AB,E为垂足,若∠A=125°,则∠BCE= .
【思路点拨】平行四边形的邻角互补,∠A=125°,求∠B的度数,CE⊥AB,∠B与∠BCE互余,求∠BCE的度数.【自主解答】∵四边形ABCD是平行四边形,
∠A=125°,∴∠B=180°-∠A=55°,∵CE⊥AB,
∴∠B+∠BCE=90°,∴∠BCE=90°-∠B=35°.
答案:35°【总结提升】平行四边形中的边、角关系
1.平行四边形的对边平行且相等.
2.平行四边形的对角相等、邻角互补.题组一:平行四边形的性质定理
1.如图,E是?ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是 ( )
A.AD=CF B.BF=CF
C.AF=CD D.DE=EF【解析】选B.∵四边形ABCD是平行四边形,∴AD=BC,∠B=∠D,
AB∥CD.∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.
∵AE=ED,∴△AEF≌△DEC.∴AF=CD,EF=EC.∵∠FCD=∠D,
∴CE=DE.∴EF=DE.故C,D都成立;
∵∠B=∠D=∠F,则CF=BC=AD.故A成立.
没有条件证明BF=CF.2.如图所示,在?ABCD中,AB=2AD,且E为CD的中点,求∠AEB的度数.
【解析】∵四边形ABCD是平行四边形,
∴CD=AB,
∵DE= DC,AD= AB= DC,∴AD=DE,
∴∠DAE=∠DEA,又∵DC∥AB,∴∠DEA=∠EAB,
∴∠DAE=∠EAB,
∴∠EAB= ∠DAB,
同理得,∠ABE= ∠ABC.
∵AD∥BC,∴∠DAB+∠ABC=180°,
∴∠EAB+∠ABE= (∠DAB+∠ABC)=90°,
∴∠AEB=180°-(∠EAB+∠ABE)=90°.3.如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.【证明】∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,∴∠B=∠DCF,
在△ABE和△DCF中,
∴△ABE≌△DCF(SAS),
∴∠BAE=∠CDF.4.已知:如图,在?ABCD中,延长AB到点E,
使BE=AB,连接DE交BC于点F.
求证:△BEF≌△CDF.
【证明】∵四边形ABCD为平行四边形,
∴CD=AB,CD∥AB,∴∠E=∠FDC,
又∵BE=AB,∴CD=BE.
又∵∠DFC=∠EFB,
∴△BEF≌△CDF(AAS).题组二:平行四边形的边、角性质的应用
1.已知平行四边形ABCD中,∠B=4∠A,则∠C= ( )
A.18° B.36° C.72° D.144°【解析】选B.
因为四边形ABCD是平行四边形,
所以∠C=∠A,BC∥AD,
所以∠A+∠B=180°,
因为∠B=4∠A,所以∠A=36°,
所以∠C=∠A=36°.
故选B.2.如图,在?ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1= ( )
A.40° B.50° C.60° D.80°【解析】选B.∵AD∥BC,∠B=80°,
∴∠BAD=180°-∠B=100°.
∵AE平分∠BAD,
∴∠DAE= ∠BAD=50°.
∴∠AEB=∠DAE=50°,
∵CF∥AE,∴∠1=∠AEB=50°.3.已知?ABCD的周长为32,AB=4,则BC= ( )
A.4 B.12 C.24 D.28
【解析】选B.∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长是32,AB=4,
∴2(AB+BC)=32,∴BC=12.4.在?ABCD中,若∠A =2∠B,则∠B= .
【解析】∵四边形ABCD是平行四边形,
∴∠A+∠B=180°.
∵∠A =2∠B,∴∠B=60°.
答案:60°5.如图,在平行四边形ABCD中,AB=5cm,AD=
7cm,∠ABC的平分线交AD于点E,交CD的延长
线于点F,则DF= cm.
【解析】由四边形ABCD为平行四边形可知,
AB∥CD,∴∠ABF=∠CFB,又∵∠ABF=∠CBF,
∴∠CBF=∠CFB,∴CF=CB=AD=7cm,
∴DF=CF-CD=2cm.
答案:26.如图所示,?ABCD的相邻边AD∶AB=5∶4,过点A作AE⊥BC,
AF⊥CD,垂足分别为E,F,AE=4cm,求AF的长.【解析】因为S?ABCD=BC·AE=CD·AF,
所以AF=
又因为AB=CD,AD=BC,且AD∶AB=5∶4,
所以【想一想错在哪?】平行四边形的一条角平分线分对边为3和4两部分,求平行四边形的周长.
提示:本题错在没有弄清楚哪一部分为3,哪一部分为4,忽略了多解的情况.
2.2.1 平行四边形的性质(第1课时)1.理解平行四边形的概念和性质.(重点)
2.理解两条平行线间的距离.(重点)
3.会用平行四边形的性质进行计算或证明.(重点、难点)一、平行四边形的定义及表示方法
1.定义:两组对边分别_____的四边形.
2.表示:平行四边形用“__”表示,如图,平行四边形ABCD记作
“ ______”.平行??ABCD二、平行四边形的性质
1.根据定义画一个平行四边形,如图所示:
2.思考:度量如图中平行四边形的两组对边、两组对角,猜想平行四边形的对边有什么数量关系?对角呢?
提示:平行四边形的对边相等,对角相等.3.证明猜想:
(1)证明线段、角相等的一般方法是利用三角形全等,怎样构造
三角形?
提示:连接AC.
(2)由平行四边形的定义及AC是公共边,易得△ABC___△CDA.
(3)由此可得到哪些相等的线段、角?
提示:AD=CB,AB=CD,∠B=∠D,∠BAD=∠DCB.≌【总结】平行四边形的性质:平行四边形的对边_____;平行四
边形的对角_____.相等相等三、两条平行线之间的距离
两条平行线中,一条直线上_________到另一条直线的距离.任意一点 (打“√”或“×”)
(1)平行四边形的邻边相等. ( )
(2)平行四边形的邻角相等. ( )
(3)一组对边平行的四边形是平行四边形. ( )
(4)夹在两条平行线间的平行线段相等. ( ) ×××√知识点 1 平行四边形的性质定理?
【例1】如图,平行四边形ABCD中,E,F分别是AB,CD上的点,且AE=CF,证明:DE=BF.【教你解题】【总结提升】平行四边形的性质定理的应用
1.利用平行四边形的性质是证明线段(或角)相等的一种常用方法.应用时注意挖掘隐含条件:平行四边形的对边平行且相等;对角相等、邻角互补.
2.常常结合全等三角形、平行线的性质等知识进行综合考查.知识点 2 平行四边形的边、角性质的应用?
【例2】如图,在?ABCD中,CE⊥AB,E为垂足,若∠A=125°,则∠BCE= .
【思路点拨】平行四边形的邻角互补,∠A=125°,求∠B的度数,CE⊥AB,∠B与∠BCE互余,求∠BCE的度数.【自主解答】∵四边形ABCD是平行四边形,
∠A=125°,∴∠B=180°-∠A=55°,∵CE⊥AB,
∴∠B+∠BCE=90°,∴∠BCE=90°-∠B=35°.
答案:35°【总结提升】平行四边形中的边、角关系
1.平行四边形的对边平行且相等.
2.平行四边形的对角相等、邻角互补.题组一:平行四边形的性质定理
1.如图,E是?ABCD的边AD的中点,CE与BA的延长线交于点F,若∠FCD=∠D,则下列结论不成立的是 ( )
A.AD=CF B.BF=CF
C.AF=CD D.DE=EF【解析】选B.∵四边形ABCD是平行四边形,∴AD=BC,∠B=∠D,
AB∥CD.∵BF∥CD,∴∠F=∠FCD,∠FAE=∠D.
∵AE=ED,∴△AEF≌△DEC.∴AF=CD,EF=EC.∵∠FCD=∠D,
∴CE=DE.∴EF=DE.故C,D都成立;
∵∠B=∠D=∠F,则CF=BC=AD.故A成立.
没有条件证明BF=CF.2.如图所示,在?ABCD中,AB=2AD,且E为CD的中点,求∠AEB的度数.
【解析】∵四边形ABCD是平行四边形,
∴CD=AB,
∵DE= DC,AD= AB= DC,∴AD=DE,
∴∠DAE=∠DEA,又∵DC∥AB,∴∠DEA=∠EAB,
∴∠DAE=∠EAB,
∴∠EAB= ∠DAB,
同理得,∠ABE= ∠ABC.
∵AD∥BC,∴∠DAB+∠ABC=180°,
∴∠EAB+∠ABE= (∠DAB+∠ABC)=90°,
∴∠AEB=180°-(∠EAB+∠ABE)=90°.3.如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.求证:∠BAE=∠CDF.【证明】∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,∴∠B=∠DCF,
在△ABE和△DCF中,
∴△ABE≌△DCF(SAS),
∴∠BAE=∠CDF.4.已知:如图,在?ABCD中,延长AB到点E,
使BE=AB,连接DE交BC于点F.
求证:△BEF≌△CDF.
【证明】∵四边形ABCD为平行四边形,
∴CD=AB,CD∥AB,∴∠E=∠FDC,
又∵BE=AB,∴CD=BE.
又∵∠DFC=∠EFB,
∴△BEF≌△CDF(AAS).题组二:平行四边形的边、角性质的应用
1.已知平行四边形ABCD中,∠B=4∠A,则∠C= ( )
A.18° B.36° C.72° D.144°【解析】选B.
因为四边形ABCD是平行四边形,
所以∠C=∠A,BC∥AD,
所以∠A+∠B=180°,
因为∠B=4∠A,所以∠A=36°,
所以∠C=∠A=36°.
故选B.2.如图,在?ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1= ( )
A.40° B.50° C.60° D.80°【解析】选B.∵AD∥BC,∠B=80°,
∴∠BAD=180°-∠B=100°.
∵AE平分∠BAD,
∴∠DAE= ∠BAD=50°.
∴∠AEB=∠DAE=50°,
∵CF∥AE,∴∠1=∠AEB=50°.3.已知?ABCD的周长为32,AB=4,则BC= ( )
A.4 B.12 C.24 D.28
【解析】选B.∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长是32,AB=4,
∴2(AB+BC)=32,∴BC=12.4.在?ABCD中,若∠A =2∠B,则∠B= .
【解析】∵四边形ABCD是平行四边形,
∴∠A+∠B=180°.
∵∠A =2∠B,∴∠B=60°.
答案:60°5.如图,在平行四边形ABCD中,AB=5cm,AD=
7cm,∠ABC的平分线交AD于点E,交CD的延长
线于点F,则DF= cm.
【解析】由四边形ABCD为平行四边形可知,
AB∥CD,∴∠ABF=∠CFB,又∵∠ABF=∠CBF,
∴∠CBF=∠CFB,∴CF=CB=AD=7cm,
∴DF=CF-CD=2cm.
答案:26.如图所示,?ABCD的相邻边AD∶AB=5∶4,过点A作AE⊥BC,
AF⊥CD,垂足分别为E,F,AE=4cm,求AF的长.【解析】因为S?ABCD=BC·AE=CD·AF,
所以AF=
又因为AB=CD,AD=BC,且AD∶AB=5∶4,
所以【想一想错在哪?】平行四边形的一条角平分线分对边为3和4两部分,求平行四边形的周长.
提示:本题错在没有弄清楚哪一部分为3,哪一部分为4,忽略了多解的情况.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
