2020湘教版八下数学第2章四边形2.2.2平行四边形的判定第1课时习题课件(37张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.2.2平行四边形的判定第1课时习题课件(37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览









文档简介
课件37张PPT。2.2.2 平行四边形的判定(第1课时) 1.熟记平行四边形的两个判定定理.(重点)
2.能应用平行四边形的判定定理证明一个四边形是平行四边形.(重点、难点)平行四边形的判定定理
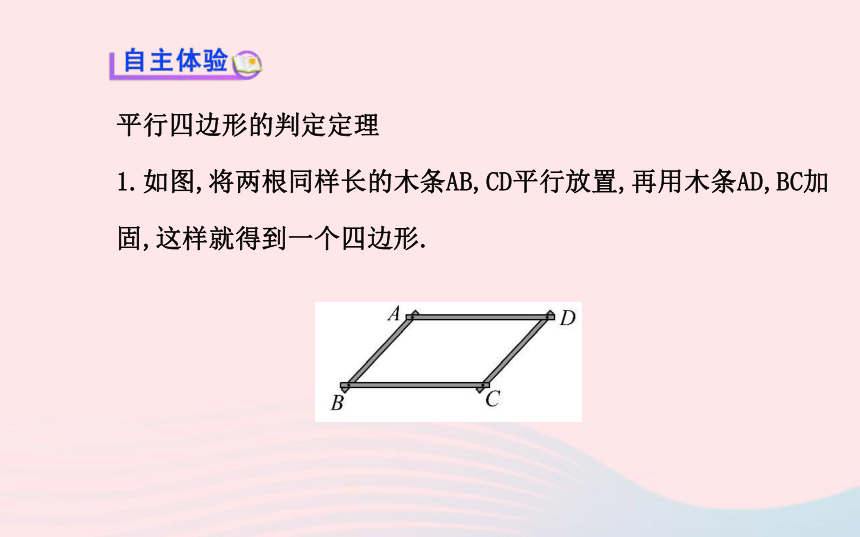
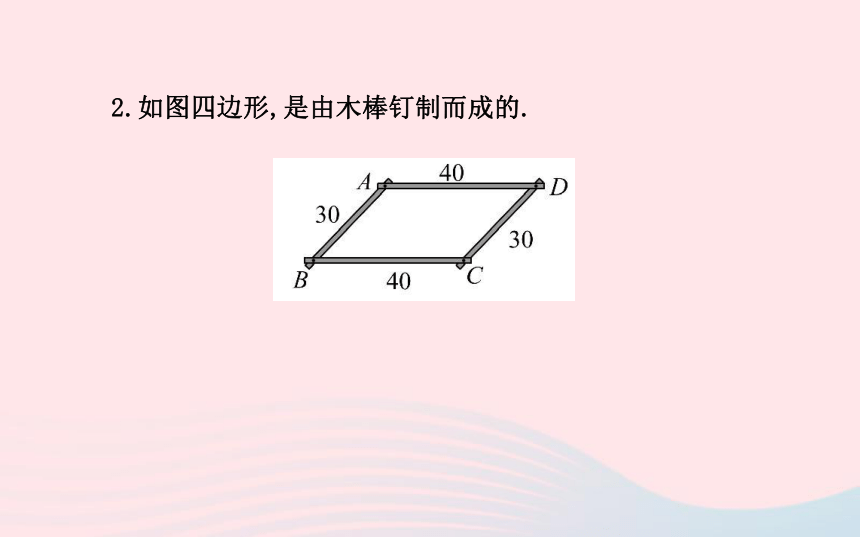
1.如图,将两根同样长的木条AB,CD平行放置,再用木条AD,BC加固,这样就得到一个四边形.2.如图四边形,是由木棒钉制而成的.【思考】(1)对于问题1,从图知看似是一个平行四边形.怎样说明它是一个平行四边形呢?
提示:只需证明四边形的两组对边分别平行,根据平行四边形的定义即可判定.
(2)你能说明问题1中四边形的形状吗?
提示:能.连接AC,∵两根木条的长度相等,∴AB=CD,又因AB∥CD,∴∠BAC=∠DCA,又因AC=CA,可证△ABC≌△CDA(SAS),故∠ACB=∠CAD,进而得AD∥BC,又已知AB∥CD,∴四边形ABCD是平行四边形.(3)对于问题2中,四边形ABCD是平行四边形吗?为什么?
提示:是.理由:连接AC,由图中可知AB=DC=30,BC=DA=40,又AC=CA,故由“SSS”得△ABC≌△CDA,又由三角形全等的性质得∠BAC=∠DCA,∠BCA=∠DAC,故AB∥CD,AD∥CB.因此由平行四边形的定义知四边形ABCD是平行四边形.【总结】
(1)平行四边形的判定定理1:一组对边___________的四边形是
平行四边形.
(2)平行四边形的判定定理2:两组对边_________的四边形是平
行四边形.平行且相等分别相等 (打“√”或“×”)
(1)一组对边平行且另一组对边相等的四边形是平行四边形.
( )
(2)三条边分别相等的四边形是平行四边形. ( )
(3)两组对边分别平行的四边形是平行四边形. ( )
(4)一组对边平行,且一组对角相等的四边形是平行四边形.( )
(5)一组对边相等,且一组对角相等的四边形是平行四边形.( )××√√×知识点 1 平行四边形判定定理1的应用?
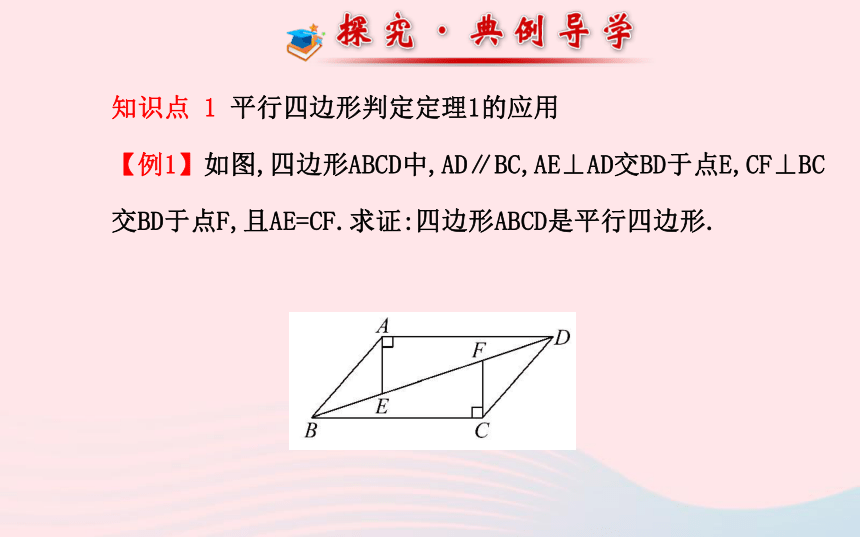
【例1】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.【解题探究】(1)当四边形中已有一组对边平行,再添加什么条件就可证明这个四边形是平行四边形?
提示:再添加这组对边相等或另一组对边平行,就可证明这个四边形是平行四边形.(2)由已知条件可知△EAD与△FCB有什么关系?为什么?
提示:全等.∵AD∥BC,
∴∠ADB=∠CBD.
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°.
∵AE=CF,
∴△EAD≌△FCB.(3)结合以上探究你能确定四边形ABCD是平行四边形吗?为什么?
提示:能.∵△EAD≌△FCB,∴AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.【互动探究】把题目中的条件“AD∥BC”改为“AD=BC”,结论还成立吗?
提示:成立.【总结提升】由一组对边平行且相等证平行四边形的几种情况
1.已知四边形中一组对边平行,通过证明三角形全等再得这组对边相等,进而证明该四边形是平行四边形.
2.已知四边形中一组对边相等,通过证明三角形全等,得角相等进而得这组对边平行,进而证明该四边形是平行四边形.知识点 2 平行四边形判定定理2的应用?
【例2】如图,在平行四边形ABCD中,点E,F分别是AD,BC的中点.
求证:(1)△ABE≌△CDF.
(2)四边形BFDE是平行四边形.【思路点拨】(1)根据平行四边形的性质和已知可证AE=CF,∠BAE=∠DCF,AB=CD,故根据SAS可证△ABE≌△CDF.
(2)由(1)可证BE=DF,由已知可证DE=BF,故可证四边形BFDE是平行四边形.【自主解答】(1)在平行四边形ABCD中,AB=CD,
AD=CB,
又∵点E,F分别是AD,BC的中点,∴AE=CF,
∵∠BAE=∠DCF,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,∴BE=DF,
又∵点E,F分别是AD,BC的中点,∴DE=BF,
∴四边形BFDE是平行四边形.【总结提升】由两组对边分别相等判定平行四边形的思路
当在欲证为平行四边形的四边形中,有一组对边相等时,一般可思考证明这组对边平行,如果无法证明这组对边平行,则只需证另一组对边相等即可.题组一:平行四边形判定定理1的应用
1.如图,在四边形ABCD中,E是BC边的中点,
连接DE并延长,交AB的延长线于F点,AB=BF.
添加一个条件,使四边形ABCD是平行四边形.
你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE【解析】选D.∵∠F=∠CDE,∴CD∥AF,
在△DEC与△FEB中,∠DCE=∠EBF,CE=BE,∠CED=∠BEF,
∴△DEC≌△FEB,
∴DC=BF,∠C=∠EBF,∴AB∥DC.
∵AB=BF,∴DC=AB,∴四边形ABCD为平行四边形.2.如图,在Rt△ABC中,∠C=90°,AC=4,将
△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED
的面积等于 .【解析】因为将△ABC沿CB向右平移得到△DEF,平移距离为2,
所以AD∥BE,AD=BE=2,
所以四边形ABED是平行四边形,
所以四边形ABED的面积=BE×AC=2×4=8.
答案:83.已知如图,?ABCD中,G,H是对角线DB上的两点,且DG=BH,DF=BE,四边形EHFG是平行四边形吗?为什么?【解析】四边形EHFG是平行四边形.
理由:在?ABCD中,AB∥CD,
∴∠BDC=∠DBA.
又∵DG=BH,DF=BE,
∴△DGF≌△BHE(SAS).
∴GF=HE,∠DGF=∠EHB.
∴∠FGH=∠EHG(等角的补角相等).
∴GF∥EH.又∵GF=EH.
∴四边形EHFG是平行四边形.4.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.【证明】∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,∴∠A=∠D,
在△AEB与△DFC中,∠AEB=∠DFC,AE=DF,∠A=∠D,∴△AEB≌△DFC(ASA),
∴BE=CF.∵BE⊥AD,CF⊥AD,∴BE∥CF.∴四边形BECF是平行四边形.5.已知,E,F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF.求证:四边形ABCD
是平行四边形.【证明】∵DF∥BE,∴∠DFA=∠BEC,
∵CF=AE,EF=EF,
∴AF=CE,
在△ADF和△CBE中,DF=BE,∠DFE=∠BEF,AF=EC,
∴△ADF≌△CBE(SAS),
∴AD=BC,∠DAC=∠BCA,∴AD∥BC,
∴四边形ABCD是平行四边形.题组二:平行四边形判定定理2的应用
1.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是 ( )
A.平行四边形 B.矩形
C.菱形 D.梯形【解析】选A.∵分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,∴AD=BC,AB=CD,∴四边形ABCD是平行四边形.2.如图,在由六个全等的正三角形拼成的图中,不重不漏的平行四边形共有 ( )
A.3个 B.4个
C.5个 D.6个【解析】选D.如图,可知,EF∥AD∥BC,ED∥FC∥AB,CD∥BE∥AF,有ED=EF=AF=AB=BC=CD=GE=GF=GA=GB=GC=GD,∴四边形EDGF,EDCG,FGBA,GCBA,EGAF,CDGB是平行四边形,共6个.3.如图,延长△ABC的中线AD至点E,使DE=AD,
连接BE,CE,则四边形ABEC的形状为 .
【解析】易证△ABD≌△ECD,△EDB≌△ADC,
故AB=CE,AC=BE,所以四边形ABEC是平行四边形.
答案:平行四边形4.如图,在四边形PONM中,MO⊥ON于O,
各边长在图中已标出,则四边形PONM
是 .
【解析】在Rt△MON中,由勾股定理,得42+(x-5)2=(x-3)2,解得x=8,所以11-x=3,x-5=3,x-3=5,所以PM=ON,PO=MN.所以四边形PONM是平行四边形.
答案:平行四边形5.若一个四边形的边长依次是a,b,c,d,且a2+b2+c2+d2=
2(ac+bd),则这个四边形是 .
【解析】已知条件可变形为(a-c)2+(b-d)2=0,所以a=c,b=d,根据两组对边分别相等可判定四边形是平行四边形.
答案:平行四边形【想一想错在哪?】如图,在△ABC中,∠ACB=90°,BC的垂直
平分线DE交BC于D,交AB于E,F在直线DE上,且AF=CE=AE.求证:四边形ACEF是平行四边形.提示:没有一组对边平行,另一组对边相等的四边形是平行四边
形的判定方法,本题可用EF?? CA或EF=CA,AF=CE进行判定.
2.能应用平行四边形的判定定理证明一个四边形是平行四边形.(重点、难点)平行四边形的判定定理
1.如图,将两根同样长的木条AB,CD平行放置,再用木条AD,BC加固,这样就得到一个四边形.2.如图四边形,是由木棒钉制而成的.【思考】(1)对于问题1,从图知看似是一个平行四边形.怎样说明它是一个平行四边形呢?
提示:只需证明四边形的两组对边分别平行,根据平行四边形的定义即可判定.
(2)你能说明问题1中四边形的形状吗?
提示:能.连接AC,∵两根木条的长度相等,∴AB=CD,又因AB∥CD,∴∠BAC=∠DCA,又因AC=CA,可证△ABC≌△CDA(SAS),故∠ACB=∠CAD,进而得AD∥BC,又已知AB∥CD,∴四边形ABCD是平行四边形.(3)对于问题2中,四边形ABCD是平行四边形吗?为什么?
提示:是.理由:连接AC,由图中可知AB=DC=30,BC=DA=40,又AC=CA,故由“SSS”得△ABC≌△CDA,又由三角形全等的性质得∠BAC=∠DCA,∠BCA=∠DAC,故AB∥CD,AD∥CB.因此由平行四边形的定义知四边形ABCD是平行四边形.【总结】
(1)平行四边形的判定定理1:一组对边___________的四边形是
平行四边形.
(2)平行四边形的判定定理2:两组对边_________的四边形是平
行四边形.平行且相等分别相等 (打“√”或“×”)
(1)一组对边平行且另一组对边相等的四边形是平行四边形.
( )
(2)三条边分别相等的四边形是平行四边形. ( )
(3)两组对边分别平行的四边形是平行四边形. ( )
(4)一组对边平行,且一组对角相等的四边形是平行四边形.( )
(5)一组对边相等,且一组对角相等的四边形是平行四边形.( )××√√×知识点 1 平行四边形判定定理1的应用?
【例1】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.【解题探究】(1)当四边形中已有一组对边平行,再添加什么条件就可证明这个四边形是平行四边形?
提示:再添加这组对边相等或另一组对边平行,就可证明这个四边形是平行四边形.(2)由已知条件可知△EAD与△FCB有什么关系?为什么?
提示:全等.∵AD∥BC,
∴∠ADB=∠CBD.
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°.
∵AE=CF,
∴△EAD≌△FCB.(3)结合以上探究你能确定四边形ABCD是平行四边形吗?为什么?
提示:能.∵△EAD≌△FCB,∴AD=CB.又∵AD∥BC,∴四边形ABCD是平行四边形.【互动探究】把题目中的条件“AD∥BC”改为“AD=BC”,结论还成立吗?
提示:成立.【总结提升】由一组对边平行且相等证平行四边形的几种情况
1.已知四边形中一组对边平行,通过证明三角形全等再得这组对边相等,进而证明该四边形是平行四边形.
2.已知四边形中一组对边相等,通过证明三角形全等,得角相等进而得这组对边平行,进而证明该四边形是平行四边形.知识点 2 平行四边形判定定理2的应用?
【例2】如图,在平行四边形ABCD中,点E,F分别是AD,BC的中点.
求证:(1)△ABE≌△CDF.
(2)四边形BFDE是平行四边形.【思路点拨】(1)根据平行四边形的性质和已知可证AE=CF,∠BAE=∠DCF,AB=CD,故根据SAS可证△ABE≌△CDF.
(2)由(1)可证BE=DF,由已知可证DE=BF,故可证四边形BFDE是平行四边形.【自主解答】(1)在平行四边形ABCD中,AB=CD,
AD=CB,
又∵点E,F分别是AD,BC的中点,∴AE=CF,
∵∠BAE=∠DCF,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,∴BE=DF,
又∵点E,F分别是AD,BC的中点,∴DE=BF,
∴四边形BFDE是平行四边形.【总结提升】由两组对边分别相等判定平行四边形的思路
当在欲证为平行四边形的四边形中,有一组对边相等时,一般可思考证明这组对边平行,如果无法证明这组对边平行,则只需证另一组对边相等即可.题组一:平行四边形判定定理1的应用
1.如图,在四边形ABCD中,E是BC边的中点,
连接DE并延长,交AB的延长线于F点,AB=BF.
添加一个条件,使四边形ABCD是平行四边形.
你认为下面四个条件中可选择的是( )
A.AD=BC B.CD=BF
C.∠A=∠C D.∠F=∠CDE【解析】选D.∵∠F=∠CDE,∴CD∥AF,
在△DEC与△FEB中,∠DCE=∠EBF,CE=BE,∠CED=∠BEF,
∴△DEC≌△FEB,
∴DC=BF,∠C=∠EBF,∴AB∥DC.
∵AB=BF,∴DC=AB,∴四边形ABCD为平行四边形.2.如图,在Rt△ABC中,∠C=90°,AC=4,将
△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED
的面积等于 .【解析】因为将△ABC沿CB向右平移得到△DEF,平移距离为2,
所以AD∥BE,AD=BE=2,
所以四边形ABED是平行四边形,
所以四边形ABED的面积=BE×AC=2×4=8.
答案:83.已知如图,?ABCD中,G,H是对角线DB上的两点,且DG=BH,DF=BE,四边形EHFG是平行四边形吗?为什么?【解析】四边形EHFG是平行四边形.
理由:在?ABCD中,AB∥CD,
∴∠BDC=∠DBA.
又∵DG=BH,DF=BE,
∴△DGF≌△BHE(SAS).
∴GF=HE,∠DGF=∠EHB.
∴∠FGH=∠EHG(等角的补角相等).
∴GF∥EH.又∵GF=EH.
∴四边形EHFG是平行四边形.4.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.【证明】∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°,
∵AB∥CD,∴∠A=∠D,
在△AEB与△DFC中,∠AEB=∠DFC,AE=DF,∠A=∠D,∴△AEB≌△DFC(ASA),
∴BE=CF.∵BE⊥AD,CF⊥AD,∴BE∥CF.∴四边形BECF是平行四边形.5.已知,E,F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF.求证:四边形ABCD
是平行四边形.【证明】∵DF∥BE,∴∠DFA=∠BEC,
∵CF=AE,EF=EF,
∴AF=CE,
在△ADF和△CBE中,DF=BE,∠DFE=∠BEF,AF=EC,
∴△ADF≌△CBE(SAS),
∴AD=BC,∠DAC=∠BCA,∴AD∥BC,
∴四边形ABCD是平行四边形.题组二:平行四边形判定定理2的应用
1.如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB,AD,CD,则四边形ABCD一定是 ( )
A.平行四边形 B.矩形
C.菱形 D.梯形【解析】选A.∵分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,∴AD=BC,AB=CD,∴四边形ABCD是平行四边形.2.如图,在由六个全等的正三角形拼成的图中,不重不漏的平行四边形共有 ( )
A.3个 B.4个
C.5个 D.6个【解析】选D.如图,可知,EF∥AD∥BC,ED∥FC∥AB,CD∥BE∥AF,有ED=EF=AF=AB=BC=CD=GE=GF=GA=GB=GC=GD,∴四边形EDGF,EDCG,FGBA,GCBA,EGAF,CDGB是平行四边形,共6个.3.如图,延长△ABC的中线AD至点E,使DE=AD,
连接BE,CE,则四边形ABEC的形状为 .
【解析】易证△ABD≌△ECD,△EDB≌△ADC,
故AB=CE,AC=BE,所以四边形ABEC是平行四边形.
答案:平行四边形4.如图,在四边形PONM中,MO⊥ON于O,
各边长在图中已标出,则四边形PONM
是 .
【解析】在Rt△MON中,由勾股定理,得42+(x-5)2=(x-3)2,解得x=8,所以11-x=3,x-5=3,x-3=5,所以PM=ON,PO=MN.所以四边形PONM是平行四边形.
答案:平行四边形5.若一个四边形的边长依次是a,b,c,d,且a2+b2+c2+d2=
2(ac+bd),则这个四边形是 .
【解析】已知条件可变形为(a-c)2+(b-d)2=0,所以a=c,b=d,根据两组对边分别相等可判定四边形是平行四边形.
答案:平行四边形【想一想错在哪?】如图,在△ABC中,∠ACB=90°,BC的垂直
平分线DE交BC于D,交AB于E,F在直线DE上,且AF=CE=AE.求证:四边形ACEF是平行四边形.提示:没有一组对边平行,另一组对边相等的四边形是平行四边
形的判定方法,本题可用EF?? CA或EF=CA,AF=CE进行判定.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
