2020湘教版八下数学第2章四边形2.2.2平行四边形的判定第2课时习题课件(33张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.2.2平行四边形的判定第2课时习题课件(33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 689.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览










文档简介
课件33张PPT。 2.2.2 平行四边形的判定(第2课时) 1.熟记平行四边形的判定定理3:对角线互相平分的四边形是平行四边形.(重点)
2.能根据平行四边形的判定定理3,判定一个四边形是否是平行四边形.(重点、难点)平行四边形的判定定理3
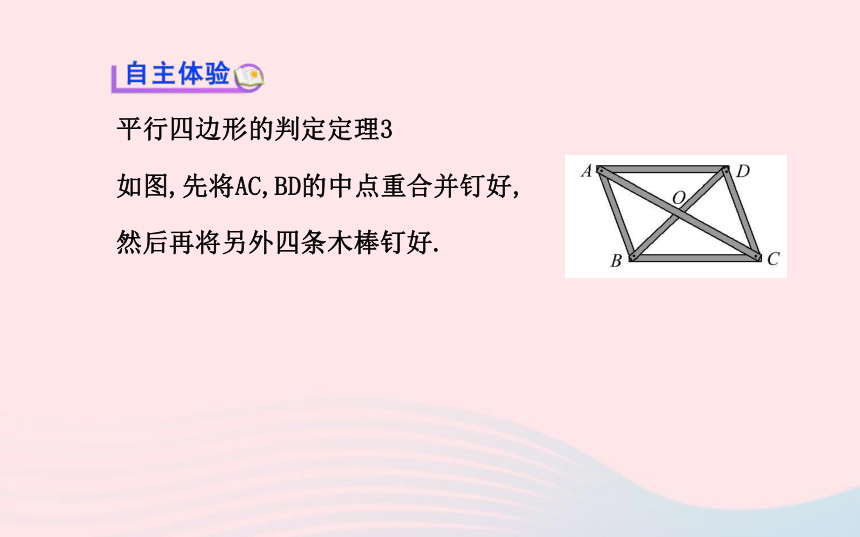
如图,先将AC,BD的中点重合并钉好,
然后再将另外四条木棒钉好.【思考】(1)图中△AOB与△COD全等吗?△AOD和△COB呢?
提示:∵点O分别是AC,BD的中点,∴AO=CO,BO=DO,又∠AOB=∠COD,∴△AOB≌△COD(SAS),同理△AOD≌△COB.
(2)AB与CD,AD与BC有何位置关系?为什么?
提示:由问题(1)知,△AOB≌△COD,∴∠BAO=∠DCO,∴由内错角相等,两直线平行,得AB∥CD,同理AD∥BC.(3)根据(2)可以得四边形ABCD是什么四边形?
提示:由问题(2)知AB∥CD,BC∥DA,由平行四边形的定义得四边形ABCD是平行四边形.【总结】平行四边形的判定定理3:
对角线_________的四边形是平行四边形.互相平分 (打“√”或“×”)
(1)对角线互相垂直的四边形是平行四边形. ( )
(2)四边形ABCD的两条对角线AC,BD交于点O,且AO=CO,则四边形
ABCD是平行四边形. ( )
(3)对角线相等的四边形是平行四边形. ( )
(4)两组角相等的四边形是平行四边形. ( )××××知识点 1 平行四边形判定定理3的应用?
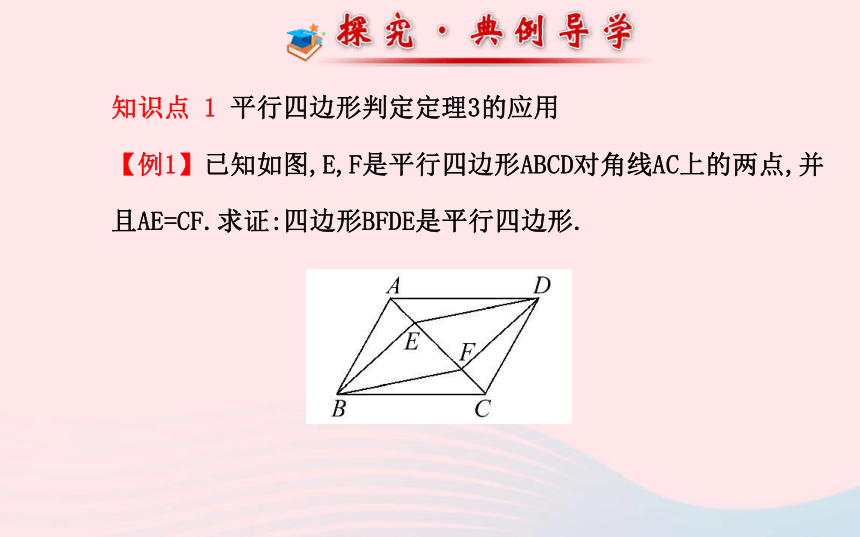
【例1】已知如图,E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.【解题探究】
(1)若利用“对角线互相平分的四边形是平行四边形”证明四边形BFDE是平行四边形,需要作辅助线:连接BD交EF于点O.
(2)因为四边形ABCD是平行四边形,
所以AO=___,BO=___.
因为AE=CF,
所以AO-AE=CO-___,
所以___=___.
又BO=___,所以四边形BFDE是平行四边形.CODOCFEOFODO【互动探究】除了利用对角线互相平分外,还有其他方法吗?
提示:利用三角形全等,得到等角,进一步得到BE∥DF,ED∥BF,由平行四边形的定义判定四边形BFDE是平行四边形.【总结提升】判定平行四边形的方法选择知识点 2 平行四边形的性质与判定的综合应用?
【例2】已知,如图,在平行
四边形ABCD中,延长DA到点E,延长BC到点F,使
得AE=CF,连接EF,分别交AB,CD于点M,N,连接
DM,BN.
(1)求证:△AEM≌△CFN.
(2)求证:四边形BMDN是平行四边形.【思路点拨】(1)?ABCD→AD∥BC,∠DAB=∠BCD,∠E=∠F,
∠EAM=∠FCN,AE=CF→△AEM≌△CFN.
(2)?ABCD→AB∥CD,AB=CD→BM∥DN,BM=DN→结论.【自主解答】(1)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∴∠EAM=∠FCN,
∵AD∥BC,∴∠E=∠F,
∵AE=CF,∴△AEM≌△CFN.
(2)由(1)得AM=CN,
又∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴BM∥DN,BM=DN,
∴四边形BMDN是平行四边形.【总结提升】平行四边形性质与判定的应用
1.利用平行四边形的性质与判定可解决以下问题:
(1)求线段的长,证明线段相等或平行,证明线段的倍分关系.
(2)求角的度数,证明角相等或互补等.
2.利用平行四边形的性质与判定解决问题时,有时需要先证一个四边形是平行四边形,再利用平行四边形的性质去解题.题组一:平行四边形判定定理3的应用
1.如图所示,D,E分别在△ABC的边AB,AC上,
F在DE延长线上,DE=EF,AE=EC,则四边形ADCF
是 ,理由是 .
【解析】DF,AC是四边形ADCF的对角线,由对角线互相平分来判定四边形ADCF是平行四边形.
答案:平行四边形 对角线互相平分的四边形是平行四边形2.已知:如图,把△ABC绕边BC的中点O旋转180°得到△DCB,求证:四边形ABDC是平行四边形.
【证明】连接OA,OD,因为△DCB是由△ABC旋转180°所得,所以点A,D,点B,C分别关于点O成中心对称,所以OB=OC,OA=OD.
所以四边形ABDC是平行四边形,
(注:还可以利用旋转变换得到AB=CD,AC=BD;或通过证明△ABC≌△DCB来证四边形ABDC是平行四边形)3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)求证:△BDE≌△CDF.
(2)请连接BF,CE,试判断四边形BECF是何种特殊四边形,并说明理由.【解析】(1)因为CF∥BE,所以∠EBD=∠FCD,
又因为∠BDE=∠CDF,BD=CD,
所以△BDE≌△CDF.
(2)四边形BECF是平行四边形.
由△BDE≌△CDF,得ED=FD.
又因为BD=CD,
所以四边形BECF是平行四边形.4.已知:如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,BO=DO.
求证:四边形ABCD是平行四边形.
【证明】∵AB∥CD,∴∠ABO=∠CDO,
在△ABO与△CDO中,∠ABO=∠CDO,BO=DO,∠AOB=∠DOC,
∴△ABO≌△CDO,∴AO=CO,∴四边形ABCD是平行四边形.5.如图,在△ABC中,D是BC上的点,O是AD的中点,过A作BC的平行线交BO的延长线于点E,则四边形ABDE是什么四边形?并说明理由.【解析】四边形ABDE是平行四边形.
理由:∵AE∥BC,
∴∠EAO=∠BDO,∠AEO=∠DBO,
∵O是AD的中点,∴AO=OD,
在△AOE和△DOB中,
∵∠EAO=∠BDO,∠AEO=∠DBO,AO=OD,
∴△AOE≌△DOB,∴OB=OE,又∵AO=OD,
∴四边形ABDE是平行四边形.题组二:平行四边形的性质与判定的综合应用
1.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A'B'C'
的位置,使B'和C重合,连接AC'交A'C于D,则△C'DC的面积为
( )
A.6 B.9 C.12 D.18【解析】选D.连接AA',由平移的性质知,AC∥A'C',AC=A'C',所
以四边形AA'C'C是平行四边形,所以点D是AC',A'C的中点,所以
A'D=CD,所以S△C'DC= S△ABC=18.2.如图,△ABC中,∠ABC=∠BAC,D是AB的中点,
EC∥AB,DE∥BC,AC与DE交于点O.下列结论中,
不一定成立的是 ( )
A.AC=DE B.AB=AC
C.AD=EC D.OA=OE【解析】选B.∵EC∥AB,DE∥BC,
∴四边形BDEC是平行四边形,
∴BD=CE,∠B=∠E.
又∵∠ABC=∠BAC,∴∠CEO=∠DAO.
又∵D是AB的中点,∴AD=BD,
∴AD=CE,∴△AOD≌△EOC,∴OA=OE.
∵BC=DE,BC=AC,∴AC=DE.
而AB=AC无法证得.3.如图,AB∥DC,AD∥BC,若∠A=35°,则∠C= .
【解析】∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,∴∠C=∠A=35°.
答案:35°4.如图,在?ABCD中,点E,F分别在边AD,BC上,
且BE∥DF,若∠EBF=45°,则∠EDF的度数
是 度.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵BE∥DF,
∴四边形BFDE是平行四边形,
∴∠EDF=∠EBF=45°.
答案:455.已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
求证:四边形MFNE是平行四边形.【证明】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
又∵DF∥BE,
∴四边形BEDF是平行四边形.
∴DE=BF.
∴AD-DE=BC-BF,即AE=CF.又∵AE∥CF,
∴四边形AFCE是平行四边形.
∴MF∥NE,
∴四边形MFNE是平行四边形.【想一想错在哪?】如图,在平行四边形ABCD中,AC交BD于
点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的关系,并说明你的结论.提示:线段BE,DF的关系包括位置关系和数量关系,本题只说明了位置关系,遗漏数量关系BE=DF.
2.能根据平行四边形的判定定理3,判定一个四边形是否是平行四边形.(重点、难点)平行四边形的判定定理3
如图,先将AC,BD的中点重合并钉好,
然后再将另外四条木棒钉好.【思考】(1)图中△AOB与△COD全等吗?△AOD和△COB呢?
提示:∵点O分别是AC,BD的中点,∴AO=CO,BO=DO,又∠AOB=∠COD,∴△AOB≌△COD(SAS),同理△AOD≌△COB.
(2)AB与CD,AD与BC有何位置关系?为什么?
提示:由问题(1)知,△AOB≌△COD,∴∠BAO=∠DCO,∴由内错角相等,两直线平行,得AB∥CD,同理AD∥BC.(3)根据(2)可以得四边形ABCD是什么四边形?
提示:由问题(2)知AB∥CD,BC∥DA,由平行四边形的定义得四边形ABCD是平行四边形.【总结】平行四边形的判定定理3:
对角线_________的四边形是平行四边形.互相平分 (打“√”或“×”)
(1)对角线互相垂直的四边形是平行四边形. ( )
(2)四边形ABCD的两条对角线AC,BD交于点O,且AO=CO,则四边形
ABCD是平行四边形. ( )
(3)对角线相等的四边形是平行四边形. ( )
(4)两组角相等的四边形是平行四边形. ( )××××知识点 1 平行四边形判定定理3的应用?
【例1】已知如图,E,F是平行四边形ABCD对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.【解题探究】
(1)若利用“对角线互相平分的四边形是平行四边形”证明四边形BFDE是平行四边形,需要作辅助线:连接BD交EF于点O.
(2)因为四边形ABCD是平行四边形,
所以AO=___,BO=___.
因为AE=CF,
所以AO-AE=CO-___,
所以___=___.
又BO=___,所以四边形BFDE是平行四边形.CODOCFEOFODO【互动探究】除了利用对角线互相平分外,还有其他方法吗?
提示:利用三角形全等,得到等角,进一步得到BE∥DF,ED∥BF,由平行四边形的定义判定四边形BFDE是平行四边形.【总结提升】判定平行四边形的方法选择知识点 2 平行四边形的性质与判定的综合应用?
【例2】已知,如图,在平行
四边形ABCD中,延长DA到点E,延长BC到点F,使
得AE=CF,连接EF,分别交AB,CD于点M,N,连接
DM,BN.
(1)求证:△AEM≌△CFN.
(2)求证:四边形BMDN是平行四边形.【思路点拨】(1)?ABCD→AD∥BC,∠DAB=∠BCD,∠E=∠F,
∠EAM=∠FCN,AE=CF→△AEM≌△CFN.
(2)?ABCD→AB∥CD,AB=CD→BM∥DN,BM=DN→结论.【自主解答】(1)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∴∠EAM=∠FCN,
∵AD∥BC,∴∠E=∠F,
∵AE=CF,∴△AEM≌△CFN.
(2)由(1)得AM=CN,
又∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴BM∥DN,BM=DN,
∴四边形BMDN是平行四边形.【总结提升】平行四边形性质与判定的应用
1.利用平行四边形的性质与判定可解决以下问题:
(1)求线段的长,证明线段相等或平行,证明线段的倍分关系.
(2)求角的度数,证明角相等或互补等.
2.利用平行四边形的性质与判定解决问题时,有时需要先证一个四边形是平行四边形,再利用平行四边形的性质去解题.题组一:平行四边形判定定理3的应用
1.如图所示,D,E分别在△ABC的边AB,AC上,
F在DE延长线上,DE=EF,AE=EC,则四边形ADCF
是 ,理由是 .
【解析】DF,AC是四边形ADCF的对角线,由对角线互相平分来判定四边形ADCF是平行四边形.
答案:平行四边形 对角线互相平分的四边形是平行四边形2.已知:如图,把△ABC绕边BC的中点O旋转180°得到△DCB,求证:四边形ABDC是平行四边形.
【证明】连接OA,OD,因为△DCB是由△ABC旋转180°所得,所以点A,D,点B,C分别关于点O成中心对称,所以OB=OC,OA=OD.
所以四边形ABDC是平行四边形,
(注:还可以利用旋转变换得到AB=CD,AC=BD;或通过证明△ABC≌△DCB来证四边形ABDC是平行四边形)3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)求证:△BDE≌△CDF.
(2)请连接BF,CE,试判断四边形BECF是何种特殊四边形,并说明理由.【解析】(1)因为CF∥BE,所以∠EBD=∠FCD,
又因为∠BDE=∠CDF,BD=CD,
所以△BDE≌△CDF.
(2)四边形BECF是平行四边形.
由△BDE≌△CDF,得ED=FD.
又因为BD=CD,
所以四边形BECF是平行四边形.4.已知:如图,在四边形ABCD中,AB∥CD,对角线AC,BD相交于点O,BO=DO.
求证:四边形ABCD是平行四边形.
【证明】∵AB∥CD,∴∠ABO=∠CDO,
在△ABO与△CDO中,∠ABO=∠CDO,BO=DO,∠AOB=∠DOC,
∴△ABO≌△CDO,∴AO=CO,∴四边形ABCD是平行四边形.5.如图,在△ABC中,D是BC上的点,O是AD的中点,过A作BC的平行线交BO的延长线于点E,则四边形ABDE是什么四边形?并说明理由.【解析】四边形ABDE是平行四边形.
理由:∵AE∥BC,
∴∠EAO=∠BDO,∠AEO=∠DBO,
∵O是AD的中点,∴AO=OD,
在△AOE和△DOB中,
∵∠EAO=∠BDO,∠AEO=∠DBO,AO=OD,
∴△AOE≌△DOB,∴OB=OE,又∵AO=OD,
∴四边形ABDE是平行四边形.题组二:平行四边形的性质与判定的综合应用
1.已知△ABC的面积为36,将△ABC沿BC的方向平移到△A'B'C'
的位置,使B'和C重合,连接AC'交A'C于D,则△C'DC的面积为
( )
A.6 B.9 C.12 D.18【解析】选D.连接AA',由平移的性质知,AC∥A'C',AC=A'C',所
以四边形AA'C'C是平行四边形,所以点D是AC',A'C的中点,所以
A'D=CD,所以S△C'DC= S△ABC=18.2.如图,△ABC中,∠ABC=∠BAC,D是AB的中点,
EC∥AB,DE∥BC,AC与DE交于点O.下列结论中,
不一定成立的是 ( )
A.AC=DE B.AB=AC
C.AD=EC D.OA=OE【解析】选B.∵EC∥AB,DE∥BC,
∴四边形BDEC是平行四边形,
∴BD=CE,∠B=∠E.
又∵∠ABC=∠BAC,∴∠CEO=∠DAO.
又∵D是AB的中点,∴AD=BD,
∴AD=CE,∴△AOD≌△EOC,∴OA=OE.
∵BC=DE,BC=AC,∴AC=DE.
而AB=AC无法证得.3.如图,AB∥DC,AD∥BC,若∠A=35°,则∠C= .
【解析】∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,∴∠C=∠A=35°.
答案:35°4.如图,在?ABCD中,点E,F分别在边AD,BC上,
且BE∥DF,若∠EBF=45°,则∠EDF的度数
是 度.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵BE∥DF,
∴四边形BFDE是平行四边形,
∴∠EDF=∠EBF=45°.
答案:455.已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
求证:四边形MFNE是平行四边形.【证明】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
又∵DF∥BE,
∴四边形BEDF是平行四边形.
∴DE=BF.
∴AD-DE=BC-BF,即AE=CF.又∵AE∥CF,
∴四边形AFCE是平行四边形.
∴MF∥NE,
∴四边形MFNE是平行四边形.【想一想错在哪?】如图,在平行四边形ABCD中,AC交BD于
点O,点E,点F分别是OA,OC的中点,请判断线段BE,DF的关系,并说明你的结论.提示:线段BE,DF的关系包括位置关系和数量关系,本题只说明了位置关系,遗漏数量关系BE=DF.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
