2020湘教版八下数学第2章四边形2.6.1菱形的性质习题课件(36张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.6.1菱形的性质习题课件(36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 768.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览









文档简介
课件36张PPT。2.6 菱 形?
2.6.1 菱形的性质1.掌握菱形的性质.(重点)
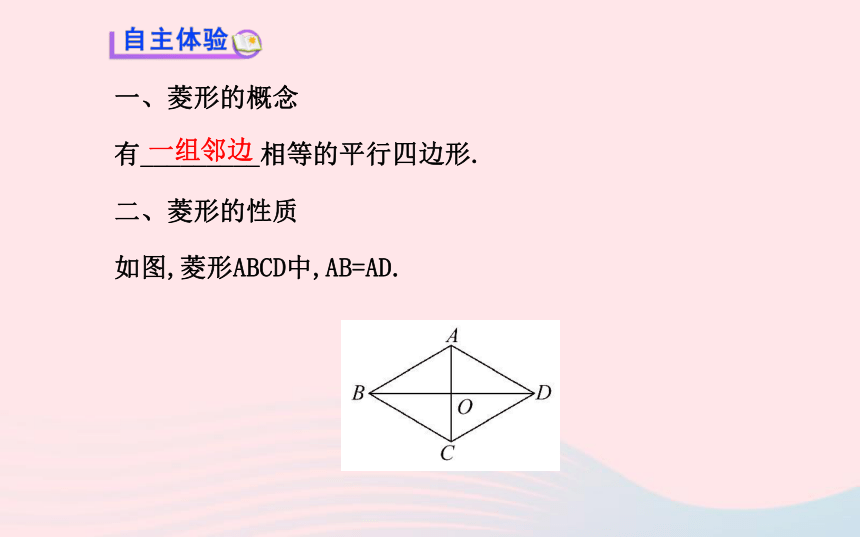
2.会用菱形的性质进行计算或证明.(重点、难点)一、菱形的概念
有_________相等的平行四边形.
二、菱形的性质
如图,菱形ABCD中,AB=AD.一组邻边∵四边形ABCD是菱形,也是平行四边形,
∴AB=___,AD=___,OA=___,OB=___,
又∵AB=AD,∴AB=___=AD=___,
在等腰△ABD中,∵OB=___,
∴AO___BD,且AO_____∠BAD.
同理可得OC_____∠BCD,OB平分______,OD平分______.CDBCOCODCDBCOD⊥平分平分∠ABC∠ADC【总结】菱形的性质:
(1)菱形具有平行四边形的所有性质.
(2)菱形的四条边都_____.
(3)菱形的两条对角线_____________,并且每一条对角线_____
一组对角.
(4)菱形是轴对称图形,它的_________________就是它的对称轴.
(5)菱形也是_________图形,_____________是对称中心.相等互相垂直平分平分对角线所在的直线中心对称对角线的交点 (打“√”或“×”)
(1)菱形的对角线互相垂直且相等. ( )
(2)菱形的对角线把菱形分成四个全等的直角三角形. ( )
(3)菱形的面积等于两条对角线长的乘积的一半. ( )
(4)菱形的对角相等. ( )
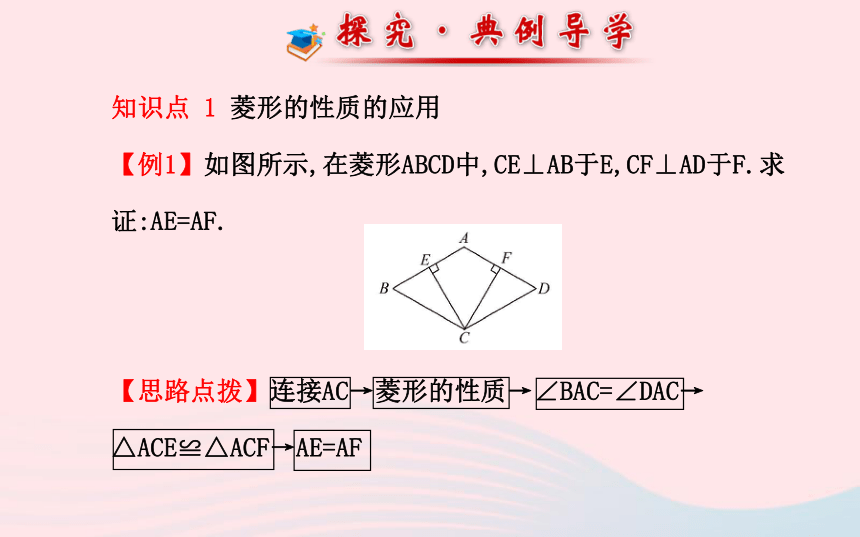
(5)菱形的邻边互相垂直. ( )×√√√×知识点 1 菱形的性质的应用?
【例1】如图所示,在菱形ABCD中,CE⊥AB于E,CF⊥AD于F.求
证:AE=AF.
【思路点拨】连接AC→菱形的性质→∠BAC=∠DAC→
△ACE≌△ACF→AE=AF【自主解答】连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
在△ACE和△ACF中,
∠AEC=∠AFC=90°,∠BAC=∠DAC,AC=AC,
∴△ACE≌△ACF.
∴AE=AF.【总结提升】菱形性质的应用
1.边、角之间的关系,可以将问题转化到全等三角形中,进行有关边、角的位置或数量关系的证明、计算.
2.对角线的性质,可以将问题转化到直角三角形或等腰三角形中,进行有关边角的证明、计算.
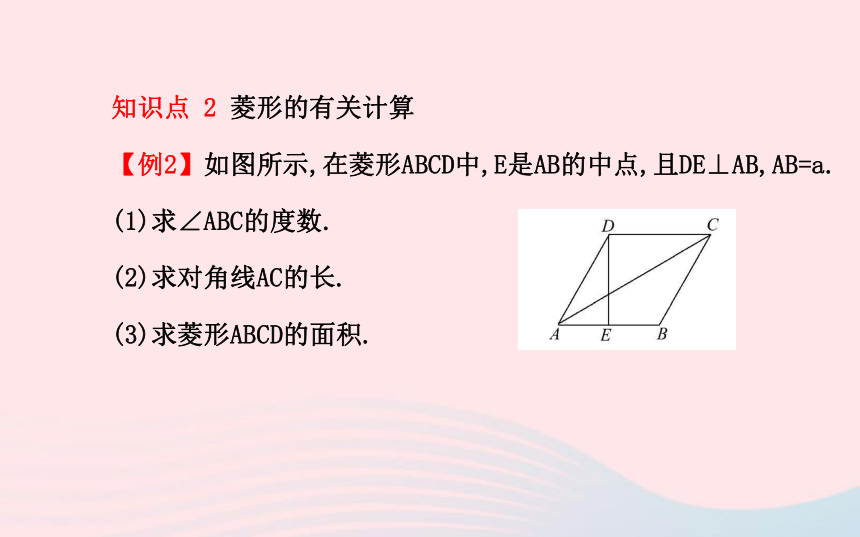
3.菱形的对角线把菱形分成4个全等的直角三角形,两对全等的等腰三角形,常结合勾股定理或等腰三角形的性质进行有关角的证明、计算,有时也与角平分线的性质结合解题.知识点 2 菱形的有关计算?
【例2】如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数.
(2)求对角线AC的长.
(3)求菱形ABCD的面积.【思路点拨】(1)连接BD,先判断△ABD的形状,再求∠ABC的度数.
(2)先求BO的长,再由勾股定理计算AO的长,进而得AC的长.
(3)由菱形的面积等于两对角线长乘积的一半,求菱形ABCD的面积.
【自主解答】(1)连接BD,交AC于点O.∵四边形ABCD是菱形,∴AD=AB.∵E是AB的中点,且DE⊥AB,∴AD=BD,∴△ABD是等边三角形,∴∠ABC=60°×2=120°.(2)∵四边形ABCD是菱形,∴AC,BD互相垂直平分,
∴
∴OA=
∴AC=2AO=
(3)S菱形ABCD=【总结提升】菱形的相关计算
如果菱形两对角线长为a,b,则其边长为 周长为
面积为题组一:菱形的性质的应用
1.如图,在菱形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OC
【解析】选B.菱形的对边平行且相等,所以AB∥DC;菱形的对角线一定垂直,所以AC⊥BD;菱形的对角线互相平分,所以OA=OC;菱形的对角线不一定相等.2.如图,在菱形ABCD中,∠BAD=
2∠B,E,F分别为BC,CD的中点,连接AE,AC,AF,则
图中与△ABE全等的三角形(△ABE除外)有( )
A.1个 B.2个 C.3个 D.4个
【解析】选C.先由菱形的性质得出AD∥BC,由平行线的性质得
到∠BAD+∠B=180°,又∠BAD=2∠B,求出∠B=60°,则∠D=∠B
=60°,△ABC与△ACD是全等的等边三角形,再根据E,F分别为
BC,CD的中点,即可求出与△ABE全等的三角形(△ABE除外)有
△ACE,△ACF,△ADF.3.如图所示,在平面直角坐标系中,菱形MNPO
的顶点P的坐标是(3,4),则顶点M,N的坐标分
别是 ( )
A.M(5,0),N(8,4)
B.M(4,0),N(8,4)
C.M(5,0),N(7,4)
D.M(4,0),N(7,4)【解析】选A.过P作PE⊥OM,∵顶点P的坐标
是(3,4),∴OE=3,PE=4,∴OP=5,∵四边形
MNPO是菱形,∴OM=OP=5,∴点M的坐标为
(5,0),过点N作NF⊥OM于点F,则△POE≌△NMF,
∴MF=OE=3,∴OF=5+3=8,∴点N的坐标为(8,4).4.如图,菱形ABCD的对角线的长分别是2和5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .【解析】由条件知PE∥BC,PF∥CD,可得PE∥AF,PF∥AE,
∴四边形AEPF为平行四边形,这样容易得到S△POF=S△AOE,
∴S阴影=S△ABC=
答案:5.如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线
于点E.求证:DE= BE.【证明】∵ABCD是菱形,
∴AD∥BC,AB=BC=CD=DA.
又∵∠ABC=60°,∴BC=AC=AD.
∵DE∥AC,∴ACED为平行四边形.
∴CE=AD=BC,DE=AC.
∴DE=CE=BC,∴DE= BE.6.如图,菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,
∠BAE=18°,求∠CEF的度数.【解析】连接AC.∵四边形ABCD是菱形,
∴AB=BC,∠ACB=∠ACF.
又∵∠B=60°,∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC.
∴∠ACF=∠B=60°.
∵∠EAF=∠BAC=60°,
∴∠BAE=∠CAF,∴△ABE≌△ACF,
∴AE=AF,∴△AEF是等边三角形,
∴∠AEF=60°.
又∵∠AEF+∠CEF=∠B+∠BAE,∠BAE=18°,
∴∠CEF=18°.题组二:菱形的有关计算
1.如图,菱形ABCD的两条
对角线相交于O,若AC=6,BD=4,则菱形ABCD
的周长是( )
【解析】选C.∵四边形ABCD是菱形,AC=6,BD=4,
∴AC⊥BD,OA= AC=3,OB= BD=2,AB=BC=CD=AD,
∴在Rt△AOB中, ∴菱形的周长是2.如图,在菱形ABCD中,
∠BAD=80°,AB的垂直平分线交对角线AC
于点F,垂足为E,连接DF,则∠CDF等于( )
A.50° B.60°
C.70° D.80°【解析】选B.如图,连接BF,∵在菱形ABCD中,∠BAD=80°,
∴∠FAB=∠DCF=40°,∵EF垂直平分AB,∴AF=BF,则∠FAB=
∠FBA=40°,∴∠CFB=∠FAB+∠FBA=80°,∴在△CDF中,
∠CDF=60°.3.如图,在菱形ABCD中,
∠BAD=120°.已知△ABC的周长是15,则菱
形ABCD的周长是 ( )
A.25 B.20
C.15 D.10
【解析】选B.∵AC是菱形ABCD的对角线,∠BAD=120°,
∴∠BAC=60°.∵AB=BC,∴△ABC是等边三角形.∵△ABC的周长
是15,∴边长AB=5.∴菱形ABCD的周长为5×4=20.【归纳整合】含有60°或120°内角的菱形的性质
(1)短的对角线与菱形相邻的两边构成的三角形是等边三角形.
(2)菱形的两条对角线把菱形分成的四个全等的直角三角形中
的较小锐角为30°,可利用这一特殊边角关系解决问题.
(3)如果菱形的边长为a,那么菱形的面积为4.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为 cm2.【解析】因为E是AB的中点,所以AE=1 cm,又因为DE⊥AB,
所以在Rt△ADE中,
DE=
所以菱形的面积为
答案:5.如图,在菱形ABCD中,E是AB的中点,作
EF∥BC,交AC于点F.如果EF=4,求CD.
【解析】∵E为AB的中点,EF∥BC,∴F为AC的中点,
∴EF= BC,又EF=4,∴BC=8,∵四边形ABCD为菱形,∴BC=CD,∴CD=8.6.若菱形ABCD的周长为12cm,相邻两角的比为5∶1,那么菱形对边间的距离是多少?
【解析】如图,过A作AE⊥BC,∵∠BAD∶∠B
=5∶1且∠BAD+∠B=180°,∴∠B=30°,
∴AE= AB,
∵菱形ABCD的周长是12cm,∴AB=12÷4=3(cm),
∴AE= cm.7.已知菱形的周长为40cm,两条对角线之比为3∶4,求菱形的面积.【解析】如图,∵菱形ABCD的周长是40cm,∴AB=10cm.
∵OA= AC,OB= BD,
AC∶BD=4∶3,
∴OA∶OB=4∶3.
设OA=4x,OB=3x,由勾股定理,得(4x)2+(3x)2=102,解得x=2.那么
OA=8,OB=6.∴AC=16,BD=12,
S菱形ABCD= AC·BD= ×16×12=96(cm2).【想一想错在哪?】已知菱形的周长为24,一条对角线长为8,求菱形的面积.
提示:菱形的面积等于两条对角线长的乘积的一半.
2.6.1 菱形的性质1.掌握菱形的性质.(重点)
2.会用菱形的性质进行计算或证明.(重点、难点)一、菱形的概念
有_________相等的平行四边形.
二、菱形的性质
如图,菱形ABCD中,AB=AD.一组邻边∵四边形ABCD是菱形,也是平行四边形,
∴AB=___,AD=___,OA=___,OB=___,
又∵AB=AD,∴AB=___=AD=___,
在等腰△ABD中,∵OB=___,
∴AO___BD,且AO_____∠BAD.
同理可得OC_____∠BCD,OB平分______,OD平分______.CDBCOCODCDBCOD⊥平分平分∠ABC∠ADC【总结】菱形的性质:
(1)菱形具有平行四边形的所有性质.
(2)菱形的四条边都_____.
(3)菱形的两条对角线_____________,并且每一条对角线_____
一组对角.
(4)菱形是轴对称图形,它的_________________就是它的对称轴.
(5)菱形也是_________图形,_____________是对称中心.相等互相垂直平分平分对角线所在的直线中心对称对角线的交点 (打“√”或“×”)
(1)菱形的对角线互相垂直且相等. ( )
(2)菱形的对角线把菱形分成四个全等的直角三角形. ( )
(3)菱形的面积等于两条对角线长的乘积的一半. ( )
(4)菱形的对角相等. ( )
(5)菱形的邻边互相垂直. ( )×√√√×知识点 1 菱形的性质的应用?
【例1】如图所示,在菱形ABCD中,CE⊥AB于E,CF⊥AD于F.求
证:AE=AF.
【思路点拨】连接AC→菱形的性质→∠BAC=∠DAC→
△ACE≌△ACF→AE=AF【自主解答】连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
在△ACE和△ACF中,
∠AEC=∠AFC=90°,∠BAC=∠DAC,AC=AC,
∴△ACE≌△ACF.
∴AE=AF.【总结提升】菱形性质的应用
1.边、角之间的关系,可以将问题转化到全等三角形中,进行有关边、角的位置或数量关系的证明、计算.
2.对角线的性质,可以将问题转化到直角三角形或等腰三角形中,进行有关边角的证明、计算.
3.菱形的对角线把菱形分成4个全等的直角三角形,两对全等的等腰三角形,常结合勾股定理或等腰三角形的性质进行有关角的证明、计算,有时也与角平分线的性质结合解题.知识点 2 菱形的有关计算?
【例2】如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数.
(2)求对角线AC的长.
(3)求菱形ABCD的面积.【思路点拨】(1)连接BD,先判断△ABD的形状,再求∠ABC的度数.
(2)先求BO的长,再由勾股定理计算AO的长,进而得AC的长.
(3)由菱形的面积等于两对角线长乘积的一半,求菱形ABCD的面积.
【自主解答】(1)连接BD,交AC于点O.∵四边形ABCD是菱形,∴AD=AB.∵E是AB的中点,且DE⊥AB,∴AD=BD,∴△ABD是等边三角形,∴∠ABC=60°×2=120°.(2)∵四边形ABCD是菱形,∴AC,BD互相垂直平分,
∴
∴OA=
∴AC=2AO=
(3)S菱形ABCD=【总结提升】菱形的相关计算
如果菱形两对角线长为a,b,则其边长为 周长为
面积为题组一:菱形的性质的应用
1.如图,在菱形ABCD中,对角线AC,BD交于点O,
下列说法错误的是 ( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.OA=OC
【解析】选B.菱形的对边平行且相等,所以AB∥DC;菱形的对角线一定垂直,所以AC⊥BD;菱形的对角线互相平分,所以OA=OC;菱形的对角线不一定相等.2.如图,在菱形ABCD中,∠BAD=
2∠B,E,F分别为BC,CD的中点,连接AE,AC,AF,则
图中与△ABE全等的三角形(△ABE除外)有( )
A.1个 B.2个 C.3个 D.4个
【解析】选C.先由菱形的性质得出AD∥BC,由平行线的性质得
到∠BAD+∠B=180°,又∠BAD=2∠B,求出∠B=60°,则∠D=∠B
=60°,△ABC与△ACD是全等的等边三角形,再根据E,F分别为
BC,CD的中点,即可求出与△ABE全等的三角形(△ABE除外)有
△ACE,△ACF,△ADF.3.如图所示,在平面直角坐标系中,菱形MNPO
的顶点P的坐标是(3,4),则顶点M,N的坐标分
别是 ( )
A.M(5,0),N(8,4)
B.M(4,0),N(8,4)
C.M(5,0),N(7,4)
D.M(4,0),N(7,4)【解析】选A.过P作PE⊥OM,∵顶点P的坐标
是(3,4),∴OE=3,PE=4,∴OP=5,∵四边形
MNPO是菱形,∴OM=OP=5,∴点M的坐标为
(5,0),过点N作NF⊥OM于点F,则△POE≌△NMF,
∴MF=OE=3,∴OF=5+3=8,∴点N的坐标为(8,4).4.如图,菱形ABCD的对角线的长分别是2和5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于点E,PF∥CD交AD于点F,则阴影部分的面积是 .【解析】由条件知PE∥BC,PF∥CD,可得PE∥AF,PF∥AE,
∴四边形AEPF为平行四边形,这样容易得到S△POF=S△AOE,
∴S阴影=S△ABC=
答案:5.如图所示,在菱形ABCD中,∠ABC=60°,DE∥AC交BC的延长线
于点E.求证:DE= BE.【证明】∵ABCD是菱形,
∴AD∥BC,AB=BC=CD=DA.
又∵∠ABC=60°,∴BC=AC=AD.
∵DE∥AC,∴ACED为平行四边形.
∴CE=AD=BC,DE=AC.
∴DE=CE=BC,∴DE= BE.6.如图,菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,
∠BAE=18°,求∠CEF的度数.【解析】连接AC.∵四边形ABCD是菱形,
∴AB=BC,∠ACB=∠ACF.
又∵∠B=60°,∴△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC.
∴∠ACF=∠B=60°.
∵∠EAF=∠BAC=60°,
∴∠BAE=∠CAF,∴△ABE≌△ACF,
∴AE=AF,∴△AEF是等边三角形,
∴∠AEF=60°.
又∵∠AEF+∠CEF=∠B+∠BAE,∠BAE=18°,
∴∠CEF=18°.题组二:菱形的有关计算
1.如图,菱形ABCD的两条
对角线相交于O,若AC=6,BD=4,则菱形ABCD
的周长是( )
【解析】选C.∵四边形ABCD是菱形,AC=6,BD=4,
∴AC⊥BD,OA= AC=3,OB= BD=2,AB=BC=CD=AD,
∴在Rt△AOB中, ∴菱形的周长是2.如图,在菱形ABCD中,
∠BAD=80°,AB的垂直平分线交对角线AC
于点F,垂足为E,连接DF,则∠CDF等于( )
A.50° B.60°
C.70° D.80°【解析】选B.如图,连接BF,∵在菱形ABCD中,∠BAD=80°,
∴∠FAB=∠DCF=40°,∵EF垂直平分AB,∴AF=BF,则∠FAB=
∠FBA=40°,∴∠CFB=∠FAB+∠FBA=80°,∴在△CDF中,
∠CDF=60°.3.如图,在菱形ABCD中,
∠BAD=120°.已知△ABC的周长是15,则菱
形ABCD的周长是 ( )
A.25 B.20
C.15 D.10
【解析】选B.∵AC是菱形ABCD的对角线,∠BAD=120°,
∴∠BAC=60°.∵AB=BC,∴△ABC是等边三角形.∵△ABC的周长
是15,∴边长AB=5.∴菱形ABCD的周长为5×4=20.【归纳整合】含有60°或120°内角的菱形的性质
(1)短的对角线与菱形相邻的两边构成的三角形是等边三角形.
(2)菱形的两条对角线把菱形分成的四个全等的直角三角形中
的较小锐角为30°,可利用这一特殊边角关系解决问题.
(3)如果菱形的边长为a,那么菱形的面积为4.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为 cm2.【解析】因为E是AB的中点,所以AE=1 cm,又因为DE⊥AB,
所以在Rt△ADE中,
DE=
所以菱形的面积为
答案:5.如图,在菱形ABCD中,E是AB的中点,作
EF∥BC,交AC于点F.如果EF=4,求CD.
【解析】∵E为AB的中点,EF∥BC,∴F为AC的中点,
∴EF= BC,又EF=4,∴BC=8,∵四边形ABCD为菱形,∴BC=CD,∴CD=8.6.若菱形ABCD的周长为12cm,相邻两角的比为5∶1,那么菱形对边间的距离是多少?
【解析】如图,过A作AE⊥BC,∵∠BAD∶∠B
=5∶1且∠BAD+∠B=180°,∴∠B=30°,
∴AE= AB,
∵菱形ABCD的周长是12cm,∴AB=12÷4=3(cm),
∴AE= cm.7.已知菱形的周长为40cm,两条对角线之比为3∶4,求菱形的面积.【解析】如图,∵菱形ABCD的周长是40cm,∴AB=10cm.
∵OA= AC,OB= BD,
AC∶BD=4∶3,
∴OA∶OB=4∶3.
设OA=4x,OB=3x,由勾股定理,得(4x)2+(3x)2=102,解得x=2.那么
OA=8,OB=6.∴AC=16,BD=12,
S菱形ABCD= AC·BD= ×16×12=96(cm2).【想一想错在哪?】已知菱形的周长为24,一条对角线长为8,求菱形的面积.
提示:菱形的面积等于两条对角线长的乘积的一半.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
