2020湘教版八下数学第2章四边形2.6.2菱形的判定习题课件(27张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形2.6.2菱形的判定习题课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 668.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览








文档简介
课件27张PPT。 2.6.2 菱形的判定 1.理解菱形的判定.(重点)
2.会用菱形的性质和判定定理进行计算或证明.(重点、难点)菱形的判定
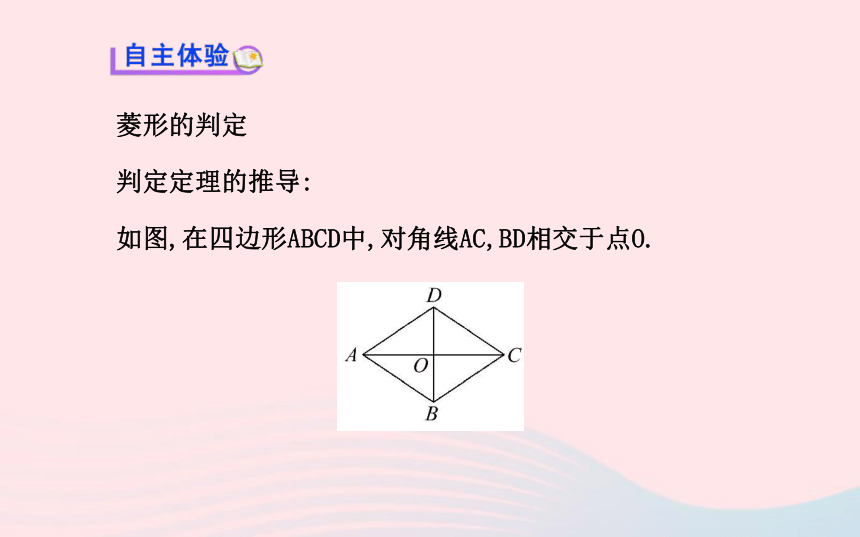
判定定理的推导:
如图,在四边形ABCD中,对角线AC,BD相交于点O.【思考】(1)如果四边形ABCD是平行四边形,且AC⊥BD,那么△AOD与△AOB有什么关系?为什么?
提示:△AOD≌△AOB.
理由:∵四边形ABCD是平行四边形,∴OD=OB,∵AC⊥BD,
∴∠AOB=∠AOD=90°,又∵OA=OA,∴△AOD≌△AOB(SAS).(2)在上述条件下,四边形ABCD是菱形吗?为什么?
提示:四边形ABCD是菱形.理由:∵△AOD≌△AOB,∴AD=AB,
又∵四边形ABCD是平行四边形,∴平行四边形ABCD是菱形.
(3)如果AB=BC=CD=DA,那么四边形ABCD是菱形吗?为什么?
提示:四边形ABCD是菱形.理由:∵AB=CD,BC=DA,∴四边形ABCD
是平行四边形,又∵AB=BC,∴四边形ABCD是菱形.【总结】菱形的判定定理:
(1)四条边都相等的四边形是菱形.
(2)对角线_________的平行四边形是菱形.互相垂直 (打“√”或“×”)
(1)一组邻边相等的四边形是菱形. ( )
(2)对角线互相平分且相等的四边形是菱形. ( )
(3)对角线互相垂直的四边形是菱形. ( )
(4)三条边相等的四边形是菱形. ( )××××知识点 菱形判定的应用?
【例】如图,在△ABC中,
AD⊥BC于点D,点D,E,F分别是BC,AB,AC的
中点.
求证:四边形AEDF是菱形.【解题探究】(1)DE∥AF吗?DF∥AE吗?为什么?
提示:DE∥AF,DF∥AE.∵点D,E,F分别是BC,AB,AC的中点,∴DE,DF是△ABC的中位线,
∴DE∥AC,DF∥AB,即DE∥AF,DF∥AE.
(2)由(1)中结论,四边形AEDF的形状如何?
提示:四边形AEDF是平行四边形.(3)AB与AC有什么关系?为什么?
提示:AB=AC.∵AD⊥BC,BD=DC,∴AD是BC的垂直平分线,∴AB=AC.
(4)由以上探究如何确定四边形AEDF是菱形?
提示:∵AB=AC,E,F分别是AB,AC的中点,∴AE=AF,又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形.【总结提升】菱形的常用判定方法
注:因菱形的特殊性在边和对角线上,因此不论是菱形的性质还是判定,一般是从“边”和“对角线”的角度解题.题组:菱形判定的应用
1.如图,若要使平行四边形ABCD成为菱形.则需要添加的条件是
( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
【解析】选C.因为一组邻边相等的平行四边形是菱形,对角线
互相垂直平分的四边形是菱形,那么可添加的条件是AB=BC.2.如图,在?ABCD中,AE,CF分别是∠BAD和
∠BCD的平分线,添加一个条件,仍无法判
断四边形AECF为菱形的是 ( )
A.AE=AF B.EF⊥AC
C.∠B=60° D.AC是∠EAF的平分线【解析】选C.由题意易证四边形AECF是平行四边形,再由菱形的判定方法知A,B选项都可判定四边形AECF是菱形;而D选项中AC是∠EAF的平分线易证AE=EC,故也能判定四边形AECF是菱形;C选项不能判定四边形AECF是菱形.3.如图,四边形ABCD的对角线AC,BD
互相垂直,则下列条件能判定四边形
ABCD为菱形的是 ( )
A.BA=BC B.AC,BD互相平分
C.AC=BD D.AB∥CD
【解析】选B.四边形ABCD中,AC,BD互相垂直,若四边形ABCD是菱形,需添加的条件是:AC,BD互相平分(对角线互相垂直且平分的四边形是菱形).4.如图所示,平行四边形
ABCD的对角线AC,BD相交于点O,试添加一个
条件: ,使得平行四边
形ABCD是菱形.
【解析】添加AC⊥BD,则对角线互相垂直的平行四边形是菱形;添加AD=DC,则一组邻边相等的平行四边形是菱形.注意这里的一组邻边相等可以用其他的一组邻边相等来取代.
答案:答案不唯一,AC⊥BD(或AD=DC)5.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD
= °.【解析】∵CD与BE互相垂直平分,
∴四边形BDEC是菱形,
∴DB=DE,CF=DF.
∵∠BDE=70°,
∴∠ABD=
∵AD⊥DB,∴∠BAD=90°-55°=35°.
∵AB垂直平分CD.
∴AC=AD,∴∠FAC=∠FAD=35°,∴∠CAD=70°.
答案:706.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.【证明】方法一:∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
由平移变换的性质,得
CF=AD=10cm,DF=AC=10cm,
∴AD=CF=AC=DF,
∴四边形ACFD是菱形.方法二:由平移变换的性质,
得AD∥CF,AD=CF=10cm,
∴四边形ACFD是平行四边形.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
∴AD=AC,
∴?ACFD是菱形.【归纳整合】菱形的判定思路
(1)分析条件判定四边形是一个平行四边形.
(2)从边或对角线的关系判定平行四边形是一个菱形,这是一般的规律和方法.利用定义证明是最常用的办法.7.如图,AD是△ABC的角平分线,过点D作DE∥AB,
DF∥AC,分别交AC,AB于点E和F.
(1)在图中画出线段DE和DF.
(2)连接EF,则线段AD和EF互相垂直平分,这是为什么?【解析】(1)如图所示:
(2)∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD,∵AB∥DE,
∴∠FAD=∠EDA,
∴∠EAD=∠EDA,
∴EA=ED,
∴平行四边形AEDF是菱形,
∴AD与EF互相垂直平分.【想一想错在哪?】如图,已知在菱形ABCD中,∠ABC=60°,点E在边BC上,∠BAE=25°.把线段AE绕点A逆时针方向旋转,使点E落在边DC上,求旋转角α的度数.提示:将△ABE绕点A逆时针旋转,使点B与点C重合,点E落在边DC上,解题时丢掉了这种情况.
2.会用菱形的性质和判定定理进行计算或证明.(重点、难点)菱形的判定
判定定理的推导:
如图,在四边形ABCD中,对角线AC,BD相交于点O.【思考】(1)如果四边形ABCD是平行四边形,且AC⊥BD,那么△AOD与△AOB有什么关系?为什么?
提示:△AOD≌△AOB.
理由:∵四边形ABCD是平行四边形,∴OD=OB,∵AC⊥BD,
∴∠AOB=∠AOD=90°,又∵OA=OA,∴△AOD≌△AOB(SAS).(2)在上述条件下,四边形ABCD是菱形吗?为什么?
提示:四边形ABCD是菱形.理由:∵△AOD≌△AOB,∴AD=AB,
又∵四边形ABCD是平行四边形,∴平行四边形ABCD是菱形.
(3)如果AB=BC=CD=DA,那么四边形ABCD是菱形吗?为什么?
提示:四边形ABCD是菱形.理由:∵AB=CD,BC=DA,∴四边形ABCD
是平行四边形,又∵AB=BC,∴四边形ABCD是菱形.【总结】菱形的判定定理:
(1)四条边都相等的四边形是菱形.
(2)对角线_________的平行四边形是菱形.互相垂直 (打“√”或“×”)
(1)一组邻边相等的四边形是菱形. ( )
(2)对角线互相平分且相等的四边形是菱形. ( )
(3)对角线互相垂直的四边形是菱形. ( )
(4)三条边相等的四边形是菱形. ( )××××知识点 菱形判定的应用?
【例】如图,在△ABC中,
AD⊥BC于点D,点D,E,F分别是BC,AB,AC的
中点.
求证:四边形AEDF是菱形.【解题探究】(1)DE∥AF吗?DF∥AE吗?为什么?
提示:DE∥AF,DF∥AE.∵点D,E,F分别是BC,AB,AC的中点,∴DE,DF是△ABC的中位线,
∴DE∥AC,DF∥AB,即DE∥AF,DF∥AE.
(2)由(1)中结论,四边形AEDF的形状如何?
提示:四边形AEDF是平行四边形.(3)AB与AC有什么关系?为什么?
提示:AB=AC.∵AD⊥BC,BD=DC,∴AD是BC的垂直平分线,∴AB=AC.
(4)由以上探究如何确定四边形AEDF是菱形?
提示:∵AB=AC,E,F分别是AB,AC的中点,∴AE=AF,又∵四边形AEDF是平行四边形,∴四边形AEDF是菱形.【总结提升】菱形的常用判定方法
注:因菱形的特殊性在边和对角线上,因此不论是菱形的性质还是判定,一般是从“边”和“对角线”的角度解题.题组:菱形判定的应用
1.如图,若要使平行四边形ABCD成为菱形.则需要添加的条件是
( )
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
【解析】选C.因为一组邻边相等的平行四边形是菱形,对角线
互相垂直平分的四边形是菱形,那么可添加的条件是AB=BC.2.如图,在?ABCD中,AE,CF分别是∠BAD和
∠BCD的平分线,添加一个条件,仍无法判
断四边形AECF为菱形的是 ( )
A.AE=AF B.EF⊥AC
C.∠B=60° D.AC是∠EAF的平分线【解析】选C.由题意易证四边形AECF是平行四边形,再由菱形的判定方法知A,B选项都可判定四边形AECF是菱形;而D选项中AC是∠EAF的平分线易证AE=EC,故也能判定四边形AECF是菱形;C选项不能判定四边形AECF是菱形.3.如图,四边形ABCD的对角线AC,BD
互相垂直,则下列条件能判定四边形
ABCD为菱形的是 ( )
A.BA=BC B.AC,BD互相平分
C.AC=BD D.AB∥CD
【解析】选B.四边形ABCD中,AC,BD互相垂直,若四边形ABCD是菱形,需添加的条件是:AC,BD互相平分(对角线互相垂直且平分的四边形是菱形).4.如图所示,平行四边形
ABCD的对角线AC,BD相交于点O,试添加一个
条件: ,使得平行四边
形ABCD是菱形.
【解析】添加AC⊥BD,则对角线互相垂直的平行四边形是菱形;添加AD=DC,则一组邻边相等的平行四边形是菱形.注意这里的一组邻边相等可以用其他的一组邻边相等来取代.
答案:答案不唯一,AC⊥BD(或AD=DC)5.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD
= °.【解析】∵CD与BE互相垂直平分,
∴四边形BDEC是菱形,
∴DB=DE,CF=DF.
∵∠BDE=70°,
∴∠ABD=
∵AD⊥DB,∴∠BAD=90°-55°=35°.
∵AB垂直平分CD.
∴AC=AD,∴∠FAC=∠FAD=35°,∴∠CAD=70°.
答案:706.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.【证明】方法一:∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
由平移变换的性质,得
CF=AD=10cm,DF=AC=10cm,
∴AD=CF=AC=DF,
∴四边形ACFD是菱形.方法二:由平移变换的性质,
得AD∥CF,AD=CF=10cm,
∴四边形ACFD是平行四边形.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=10cm.
∴AD=AC,
∴?ACFD是菱形.【归纳整合】菱形的判定思路
(1)分析条件判定四边形是一个平行四边形.
(2)从边或对角线的关系判定平行四边形是一个菱形,这是一般的规律和方法.利用定义证明是最常用的办法.7.如图,AD是△ABC的角平分线,过点D作DE∥AB,
DF∥AC,分别交AC,AB于点E和F.
(1)在图中画出线段DE和DF.
(2)连接EF,则线段AD和EF互相垂直平分,这是为什么?【解析】(1)如图所示:
(2)∵DE∥AB,DF∥AC,
∴四边形AEDF是平行四边形,
∵AD是△ABC的角平分线,
∴∠FAD=∠EAD,∵AB∥DE,
∴∠FAD=∠EDA,
∴∠EAD=∠EDA,
∴EA=ED,
∴平行四边形AEDF是菱形,
∴AD与EF互相垂直平分.【想一想错在哪?】如图,已知在菱形ABCD中,∠ABC=60°,点E在边BC上,∠BAE=25°.把线段AE绕点A逆时针方向旋转,使点E落在边DC上,求旋转角α的度数.提示:将△ABE绕点A逆时针旋转,使点B与点C重合,点E落在边DC上,解题时丢掉了这种情况.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
