2020湘教版八下数学第2章四边形阶段专题复习习题课件(30张PPT)
文档属性
| 名称 | 2020湘教版八下数学第2章四边形阶段专题复习习题课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 612.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 21:30:15 | ||
图片预览










文档简介
课件30张PPT。阶段专题复习
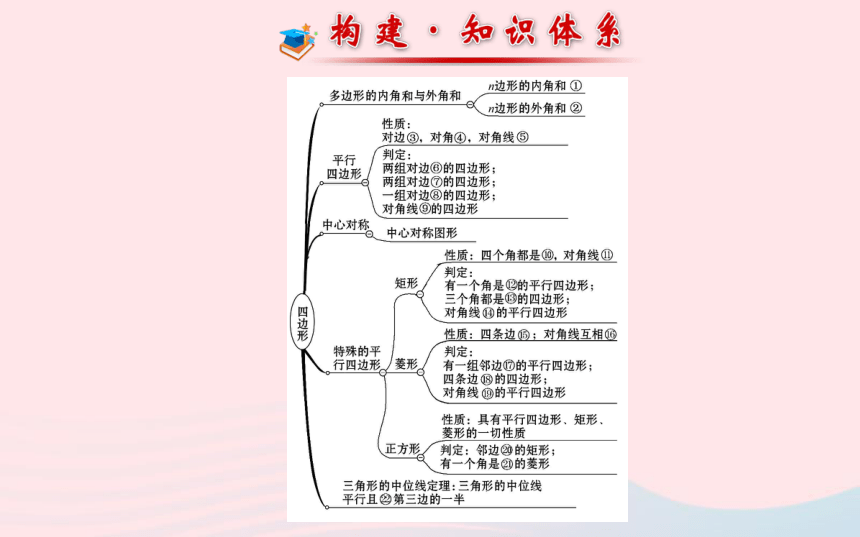
第 2 章请写出框图中数字处的内容:
①_____________;②______;③_____;④_____;⑤_________;
⑥_________;⑦_________;⑧___________;⑨_________;
⑩_____;?_____;?_____;?_____;?_____;?_____;?_____;
?_____;?_____;?_________;?_____; _____; _____.(n-2)·180°360°相等相等互相平分分别平行分别相等平行且相等互相平分直角相等直角直角相等相等垂直相等相等互相垂直相等2122直角等于考点 1 多边形的内角和与外角和?
【知识点睛】
1.n边形的内角和是(n-2)·180°.
2.任意多边形的外角和是360°.
3.内角和随着边数每增加1,其增加180°,而外角和不随边数的变化而变化.【例1】若n边形的每一个外角都等于60°,则n= .
【思路点拨】外角和360°—除以60°.
【自主解答】∵n边形的每一个外角的度数都为60°,
∴360°÷60°=6,故n边形为六边形,n=6.
答案:6【中考集训】
1.五边形的内角和为 ( )
A.720° B.540° C. 360° D. 180°
【解析】选B.(5-2)×180°=540°.2.九边形的外角和为 °.
【解析】任意多边形的外角和都是360°,故九边形的外角和为360°.
答案:3603.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
【解析】∵多边形的外角和是360°,多边形的内角和是外角和的2倍,则内角和是720°,720÷180+2=6,∴这个多边形是六边形.
答案:6考点 2 平行四边形的性质和判定?
【知识点睛】
平行四边形的性质与判定的关系两组对边分别平行
一组对边平行且相等
两组对边分别相等
两条对角线互相平分
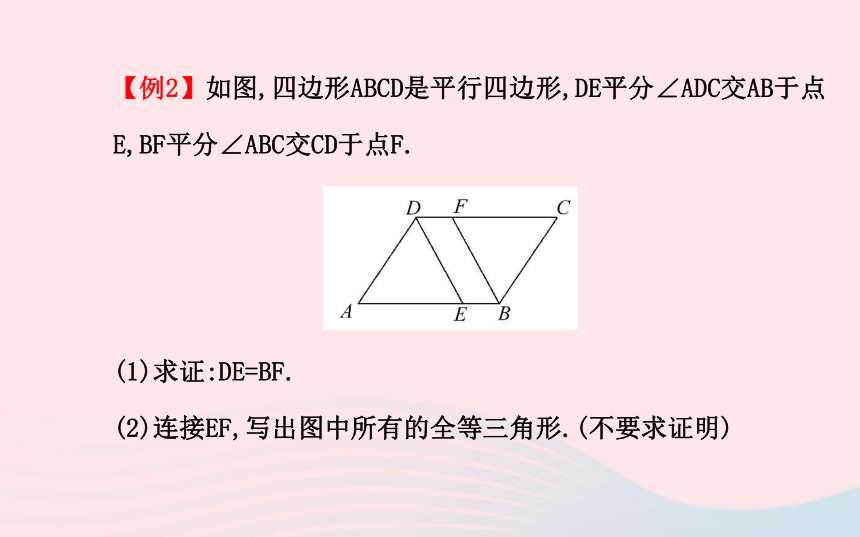
两组对角分别相等平行四边形性质判定平行四边形.【例2】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC交CD于点F.
(1)求证:DE=BF.
(2)连接EF,写出图中所有的全等三角形.(不要求证明)【思路点拨】(1)由平行四边形的性质和已知条件证明四边形DEBF是平行四边形,根据平行四边形的性质可得到DE=BF.
(2)根据三角形全等的判定条件确定全等三角形.【自主解答】(1)∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDE=∠AED,
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,∴AE=AD,
同理CF=CB,又AD=CB,AB=CD,
∴AE=CF,∴DF=BE,
∴四边形DEBF是平行四边形,∴DE=BF,(2)如图.△ADE≌△CBF,△DFE≌△BEF.【中考集训】
1.如图,在平行四边形
ABCD中,下列结论中错误的是 ( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD【解析】选D.∵在平行四边形ABCD中,
∴AB∥CD,∴∠1=∠2,故A选项正确;
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,故B,C选项正确;
无法得出AC⊥BD,故D选项错误.2.如图,在?ABCD中,
AD=2AB,CE平分∠BCD交AD边于点E,且
AE=3,则AB的长为 ( )
A.4 B.3 C. D.2
【解析】选B.根据CE平分∠BCD得∠BCE=∠ECD,AD∥BC得
∠BCE=∠DEC,从而△DCE为等腰三角形,ED=DC=AB,2AB=AD=
AE+ED=3+AB,解得AB=3.3.如图,F,C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE,BD,求证:四
边形ABDE是平行四边形.
【证明】∵AB∥DE,BC∥EF,
∴∠BAD=∠EDA,∠BCA=∠EFD.
∵AF=DC,∴AC=DF.
∴△ABC≌△DEF,∴AB=DE,
又∵AB∥DE,∴四边形ABDE是平行四边形.4.如图,已知四边形
ABDE是平行四边形,C为边BD延长线上
一点,连接AC,CE,使AB=AC.
(1)求证:△BAD≌△ACE.
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.【解析】(1)∵AB=AC,∴∠B=∠ACB.
又∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,∴∠ACB=∠CAE=∠B,
∴△BAD≌△ACE.(2)过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
∴AB=2x,
由勾股定理得,
又∵BD=10.∴BG-DG=BD,即
解得
∴S平行四边形ABDE=BD·AG=考点 3 特殊的平行四边形的性质和判定?
【知识点睛】
平行四边形、矩形、菱形、正方形性质的区别与联系
1.边:它们都具有对边平行且相等的性质,而菱形和正方形还具有四条边都相等的性质.
2.角:它们都具有对角相等且邻角互补的性质,而矩形和正方形还具有四个角都是90°的性质.3.对角线:它们都具有对角线互相平分的性质,而矩形和正方形的对角线还具有相等的性质,菱形和正方形的对角线还具有互相垂直的性质.【例3】在?ABCD中,
点E,F分别在AB,CD上,且AE=CF.
(1)求证:△ADE≌△CBF.
(2)若DF=BF,求证:四边形DEBF为菱形.【思路点拨】(1)首先根据平行四边形的性质可得AD=BC,∠A
=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF.
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行
四边形,又DF=BF,根据邻边相等的平行四边形为菱形证出结论.【自主解答】(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵AE=CF,∴△ADE≌△CBF.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF,∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∵DF=BF,∴平行四边形DEBF是菱形.
即四边形DEBF为菱形.【中考集训】
1.下列说法中,正确的是 ( )
A.同位角相等
B.对角线相等的四边形是平行四边形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直【解析】选C.只有两直线平行,同位角才相等,故A选项错误;对角线互相平分的四边形是平行四边形,故B选项错误;四条边相等的四边形是菱形,故C选项正确;矩形的对角线互相平分且相等,不一定垂直,故D选项错误.2.如图,将矩形ABCD沿对角
线BD折叠,使点C和点C'重合,若AB=2,则C'D的
长为( )
A.1 B.2
C.3 D.4
【解析】选B.在矩形ABCD中,CD=AB,
∵矩形ABCD沿对角线BD折叠后点C和点C'重合,
∴C'D=CD,∴C'D=AB,∵AB=2,∴C'D=2.3.已知:如图,在矩形ABCD
中,M,N分别是边AD,BC的中点,E,F分别是线
段BM,CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明).【解析】(1)在矩形ABCD中,AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NF=ME,∴四边形MENF是平行四边形,
由(1)得BM=CM,∴ME=MF,
∴平行四边形MENF是菱形.即四边形MENF是菱形.
(3)当AD∶AB=2∶1时,四边形MENF是正方形.
第 2 章请写出框图中数字处的内容:
①_____________;②______;③_____;④_____;⑤_________;
⑥_________;⑦_________;⑧___________;⑨_________;
⑩_____;?_____;?_____;?_____;?_____;?_____;?_____;
?_____;?_____;?_________;?_____; _____; _____.(n-2)·180°360°相等相等互相平分分别平行分别相等平行且相等互相平分直角相等直角直角相等相等垂直相等相等互相垂直相等2122直角等于考点 1 多边形的内角和与外角和?
【知识点睛】
1.n边形的内角和是(n-2)·180°.
2.任意多边形的外角和是360°.
3.内角和随着边数每增加1,其增加180°,而外角和不随边数的变化而变化.【例1】若n边形的每一个外角都等于60°,则n= .
【思路点拨】外角和360°—除以60°.
【自主解答】∵n边形的每一个外角的度数都为60°,
∴360°÷60°=6,故n边形为六边形,n=6.
答案:6【中考集训】
1.五边形的内角和为 ( )
A.720° B.540° C. 360° D. 180°
【解析】选B.(5-2)×180°=540°.2.九边形的外角和为 °.
【解析】任意多边形的外角和都是360°,故九边形的外角和为360°.
答案:3603.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
【解析】∵多边形的外角和是360°,多边形的内角和是外角和的2倍,则内角和是720°,720÷180+2=6,∴这个多边形是六边形.
答案:6考点 2 平行四边形的性质和判定?
【知识点睛】
平行四边形的性质与判定的关系两组对边分别平行
一组对边平行且相等
两组对边分别相等
两条对角线互相平分
两组对角分别相等平行四边形性质判定平行四边形.【例2】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC交CD于点F.
(1)求证:DE=BF.
(2)连接EF,写出图中所有的全等三角形.(不要求证明)【思路点拨】(1)由平行四边形的性质和已知条件证明四边形DEBF是平行四边形,根据平行四边形的性质可得到DE=BF.
(2)根据三角形全等的判定条件确定全等三角形.【自主解答】(1)∵四边形ABCD是平行四边形,
∴DC∥AB,∴∠CDE=∠AED,
∵DE平分∠ADC,∴∠ADE=∠CDE,
∴∠ADE=∠AED,∴AE=AD,
同理CF=CB,又AD=CB,AB=CD,
∴AE=CF,∴DF=BE,
∴四边形DEBF是平行四边形,∴DE=BF,(2)如图.△ADE≌△CBF,△DFE≌△BEF.【中考集训】
1.如图,在平行四边形
ABCD中,下列结论中错误的是 ( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC⊥BD【解析】选D.∵在平行四边形ABCD中,
∴AB∥CD,∴∠1=∠2,故A选项正确;
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,故B,C选项正确;
无法得出AC⊥BD,故D选项错误.2.如图,在?ABCD中,
AD=2AB,CE平分∠BCD交AD边于点E,且
AE=3,则AB的长为 ( )
A.4 B.3 C. D.2
【解析】选B.根据CE平分∠BCD得∠BCE=∠ECD,AD∥BC得
∠BCE=∠DEC,从而△DCE为等腰三角形,ED=DC=AB,2AB=AD=
AE+ED=3+AB,解得AB=3.3.如图,F,C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连接AE,BD,求证:四
边形ABDE是平行四边形.
【证明】∵AB∥DE,BC∥EF,
∴∠BAD=∠EDA,∠BCA=∠EFD.
∵AF=DC,∴AC=DF.
∴△ABC≌△DEF,∴AB=DE,
又∵AB∥DE,∴四边形ABDE是平行四边形.4.如图,已知四边形
ABDE是平行四边形,C为边BD延长线上
一点,连接AC,CE,使AB=AC.
(1)求证:△BAD≌△ACE.
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.【解析】(1)∵AB=AC,∴∠B=∠ACB.
又∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,∴∠ACB=∠CAE=∠B,
∴△BAD≌△ACE.(2)过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=45°,∴AG=DG=x,
在Rt△AGB中,∵∠B=30°,
∴AB=2x,
由勾股定理得,
又∵BD=10.∴BG-DG=BD,即
解得
∴S平行四边形ABDE=BD·AG=考点 3 特殊的平行四边形的性质和判定?
【知识点睛】
平行四边形、矩形、菱形、正方形性质的区别与联系
1.边:它们都具有对边平行且相等的性质,而菱形和正方形还具有四条边都相等的性质.
2.角:它们都具有对角相等且邻角互补的性质,而矩形和正方形还具有四个角都是90°的性质.3.对角线:它们都具有对角线互相平分的性质,而矩形和正方形的对角线还具有相等的性质,菱形和正方形的对角线还具有互相垂直的性质.【例3】在?ABCD中,
点E,F分别在AB,CD上,且AE=CF.
(1)求证:△ADE≌△CBF.
(2)若DF=BF,求证:四边形DEBF为菱形.【思路点拨】(1)首先根据平行四边形的性质可得AD=BC,∠A
=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF.
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行
四边形,又DF=BF,根据邻边相等的平行四边形为菱形证出结论.【自主解答】(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵AE=CF,∴△ADE≌△CBF.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∵AE=CF,∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∵DF=BF,∴平行四边形DEBF是菱形.
即四边形DEBF为菱形.【中考集训】
1.下列说法中,正确的是 ( )
A.同位角相等
B.对角线相等的四边形是平行四边形
C.四条边相等的四边形是菱形
D.矩形的对角线一定互相垂直【解析】选C.只有两直线平行,同位角才相等,故A选项错误;对角线互相平分的四边形是平行四边形,故B选项错误;四条边相等的四边形是菱形,故C选项正确;矩形的对角线互相平分且相等,不一定垂直,故D选项错误.2.如图,将矩形ABCD沿对角
线BD折叠,使点C和点C'重合,若AB=2,则C'D的
长为( )
A.1 B.2
C.3 D.4
【解析】选B.在矩形ABCD中,CD=AB,
∵矩形ABCD沿对角线BD折叠后点C和点C'重合,
∴C'D=CD,∴C'D=AB,∵AB=2,∴C'D=2.3.已知:如图,在矩形ABCD
中,M,N分别是边AD,BC的中点,E,F分别是线
段BM,CM的中点.
(1)求证:△ABM≌△DCM.
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
(3)当AD∶AB= 时,四边形MENF是正方形(只写结论,不需证明).【解析】(1)在矩形ABCD中,AB=CD,∠A=∠D=90°,
又∵M是AD的中点,∴AM=DM,
∴△ABM≌△DCM(SAS).
(2)四边形MENF是菱形.
证明:E,F,N分别是BM,CM,CB的中点,
∴NF∥ME,NF=ME,∴四边形MENF是平行四边形,
由(1)得BM=CM,∴ME=MF,
∴平行四边形MENF是菱形.即四边形MENF是菱形.
(3)当AD∶AB=2∶1时,四边形MENF是正方形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
