人教A版高中数学选修4-2 第二讲 一 复合变换与二阶矩阵的乘法 上课课件(共28张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-2 第二讲 一 复合变换与二阶矩阵的乘法 上课课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 726.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 21:04:41 | ||
图片预览








文档简介
(共28张PPT)
新课导入
探究
直角坐标系中,连续进行两次线性变换,其作用效果是否能用一个线性变换来表示?
是否存在一个二阶矩阵与之对应?
若存在,这个线性变换的二阶矩阵与原来两个线性变换的二阶矩阵由什么关系?
第二讲 变换的复合与二阶矩阵的乘法
2.1 复合变换与二阶矩阵的乘法
教学目标
知识与能力
掌握矩阵乘积的概念;
了解矩阵乘法的运算律,并能灵活应用.
过程与方法
通过从特殊到一般,从具体到抽象的过程,理解一般性的概念和结论.
情感态度与价值观
培养学生抽象思维能力.
教学重难点
重点:
难点:
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
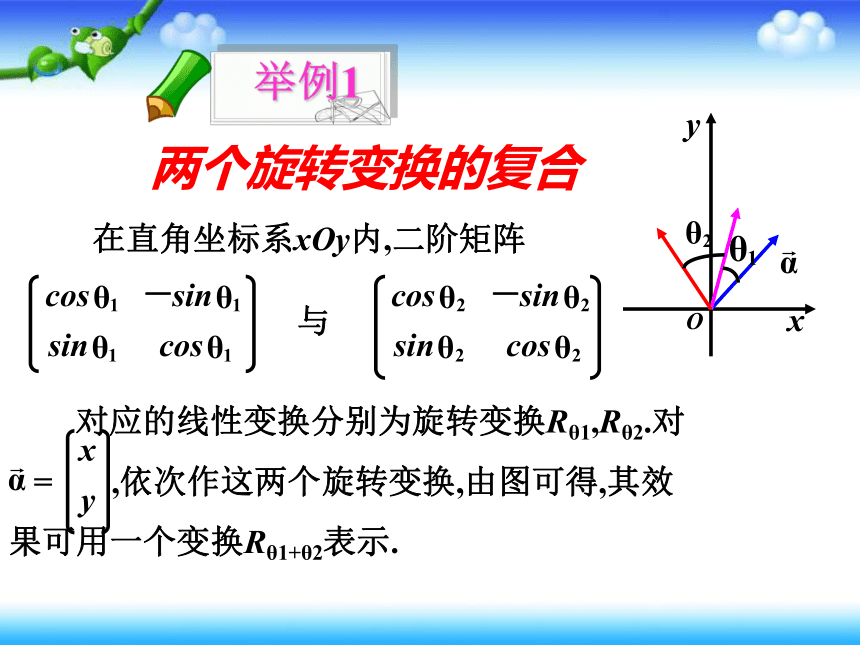
举例1
两个旋转变换的复合
在直角坐标系xOy内,二阶矩阵
与
对应的线性变换分别为旋转变换Rθ1,Rθ2.对
= ,依次作这两个旋转变换,由图可得,其效
果可用一个变换Rθ1+θ2表示.
O
y
x
∴旋转变换Rθ1+θ2是一个线性变换,对应
的矩阵为
结论
两个线性变换的复合仍然是线性变换
举例2
在直角坐标系xOy内,由矩阵B= 确定的变换是旋转变换
R30°: =
由矩阵A= 确定的变换是切变变换
ρ: =
求(1) = 先经旋转变换R30°作用,
再经切变变换ρ作用的结果.
(2)把任意一个平面向量 = 先经
旋转变换R30°作用,再经切变变换ρ作
用,变成向量 ,求 .
解:(1)R30° =
∴ρ( R30° )= =
(2)∵ R30°= =
∴ =ρ( R30° )=
=
记这个线性变换 ρ· R30° 对应的矩阵为
由例2推广至一般情况
设A= ,B= ,在直角
坐标系xOy内,对应的线性变换分别为:
f: =A =
g: =B =
对向量 = 依次作变换g,f,效果为:
=f (g ) =f (B )
=
=
=
=
定义
上述这个线性变换就称为变换g和变换f的复合变换,记为f·g.
复合变换f·g对应的矩阵为
称这个矩阵为矩阵A与B的乘积,记为AB
AB=
=
直角坐标系xOy内任意向量 ,有
结论
一一
对应
课堂小结
特殊线性变换的复合
复合前后矩阵的关系
线性变换的复合与二阶矩阵的乘积
两个线性变换的复合变换仍然是线性变换;
两个线性变换的复合变换的二阶矩阵是原来两个线性变换的“乘积”.
矩阵乘法的内在规律:
矩阵AB第一行的第一个元素等于A的第一行的元素与B的第一列的元素的乘积之和;
矩阵AB第一行的第二个元素等于A的第一行的元素与B的第二列的元素的乘积之和;
矩阵AB第二行的第一个元素等于A的第二行的元素与B的第一列的元素的乘积之和;
矩阵AB第二行的第二个元素等于A的第二行的元素与B的第二列的元素的乘积之和.
线性变换f·g的复合顺序:先做线性变换g再做线性变换f.
注意
课堂练习
1.计算:
解:
=
2.伸缩变换σ对应的矩阵A=
切变变换ρ对应的矩阵B=
将两个变换复合,得到σ·ρ.
求(1)向量 = 在复合变换σ·ρ作用下的像;
(2)复合变换σ·ρ的坐标变换公式;
(3)复合变换σ·ρ把正方形区域变成了什么图形.
解(1)(σ·ρ) =
=
=
(2)坐标变换公式: =
即:
(3)
O
y
x
1
1
∴可得到:
1
O
y
x
1
1
O
y
x
1
1
O
y
x
1
3.用矩阵的乘积证明下面等式
再见
新课导入
探究
直角坐标系中,连续进行两次线性变换,其作用效果是否能用一个线性变换来表示?
是否存在一个二阶矩阵与之对应?
若存在,这个线性变换的二阶矩阵与原来两个线性变换的二阶矩阵由什么关系?
第二讲 变换的复合与二阶矩阵的乘法
2.1 复合变换与二阶矩阵的乘法
教学目标
知识与能力
掌握矩阵乘积的概念;
了解矩阵乘法的运算律,并能灵活应用.
过程与方法
通过从特殊到一般,从具体到抽象的过程,理解一般性的概念和结论.
情感态度与价值观
培养学生抽象思维能力.
教学重难点
重点:
难点:
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
1.矩阵乘积的概念;
2.矩阵乘法的运算律.
举例1
两个旋转变换的复合
在直角坐标系xOy内,二阶矩阵
与
对应的线性变换分别为旋转变换Rθ1,Rθ2.对
= ,依次作这两个旋转变换,由图可得,其效
果可用一个变换Rθ1+θ2表示.
O
y
x
∴旋转变换Rθ1+θ2是一个线性变换,对应
的矩阵为
结论
两个线性变换的复合仍然是线性变换
举例2
在直角坐标系xOy内,由矩阵B= 确定的变换是旋转变换
R30°: =
由矩阵A= 确定的变换是切变变换
ρ: =
求(1) = 先经旋转变换R30°作用,
再经切变变换ρ作用的结果.
(2)把任意一个平面向量 = 先经
旋转变换R30°作用,再经切变变换ρ作
用,变成向量 ,求 .
解:(1)R30° =
∴ρ( R30° )= =
(2)∵ R30°= =
∴ =ρ( R30° )=
=
记这个线性变换 ρ· R30° 对应的矩阵为
由例2推广至一般情况
设A= ,B= ,在直角
坐标系xOy内,对应的线性变换分别为:
f: =A =
g: =B =
对向量 = 依次作变换g,f,效果为:
=f (g ) =f (B )
=
=
=
=
定义
上述这个线性变换就称为变换g和变换f的复合变换,记为f·g.
复合变换f·g对应的矩阵为
称这个矩阵为矩阵A与B的乘积,记为AB
AB=
=
直角坐标系xOy内任意向量 ,有
结论
一一
对应
课堂小结
特殊线性变换的复合
复合前后矩阵的关系
线性变换的复合与二阶矩阵的乘积
两个线性变换的复合变换仍然是线性变换;
两个线性变换的复合变换的二阶矩阵是原来两个线性变换的“乘积”.
矩阵乘法的内在规律:
矩阵AB第一行的第一个元素等于A的第一行的元素与B的第一列的元素的乘积之和;
矩阵AB第一行的第二个元素等于A的第一行的元素与B的第二列的元素的乘积之和;
矩阵AB第二行的第一个元素等于A的第二行的元素与B的第一列的元素的乘积之和;
矩阵AB第二行的第二个元素等于A的第二行的元素与B的第二列的元素的乘积之和.
线性变换f·g的复合顺序:先做线性变换g再做线性变换f.
注意
课堂练习
1.计算:
解:
=
2.伸缩变换σ对应的矩阵A=
切变变换ρ对应的矩阵B=
将两个变换复合,得到σ·ρ.
求(1)向量 = 在复合变换σ·ρ作用下的像;
(2)复合变换σ·ρ的坐标变换公式;
(3)复合变换σ·ρ把正方形区域变成了什么图形.
解(1)(σ·ρ) =
=
=
(2)坐标变换公式: =
即:
(3)
O
y
x
1
1
∴可得到:
1
O
y
x
1
1
O
y
x
1
1
O
y
x
1
3.用矩阵的乘积证明下面等式
再见
