人教A版高中数学选修4-2 第三讲 三 逆矩阵与二元一次方程组 上课课件(共28张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-2 第三讲 三 逆矩阵与二元一次方程组 上课课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 594.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
导入新课
在解析几何中,二元一次方程组的解的意义是什么?
直角坐标系x O y内相应的两条直线交点的坐标.
线性变换的表达式形式与二元一次方程组有很多相似的地方,能否从线性变换的角度来解释二元一次方程组的解的意义呢?
3.3 逆矩阵与二元一次方程组
二元一次方程组的矩阵形式
逆矩阵与二元一次方程组
学习重难点
用变换的观点认识解二元一次方程组的意义,会用系数矩阵的逆矩阵解系数矩阵可逆的二元一次方程组.
二元一次方程组的矩阵形式
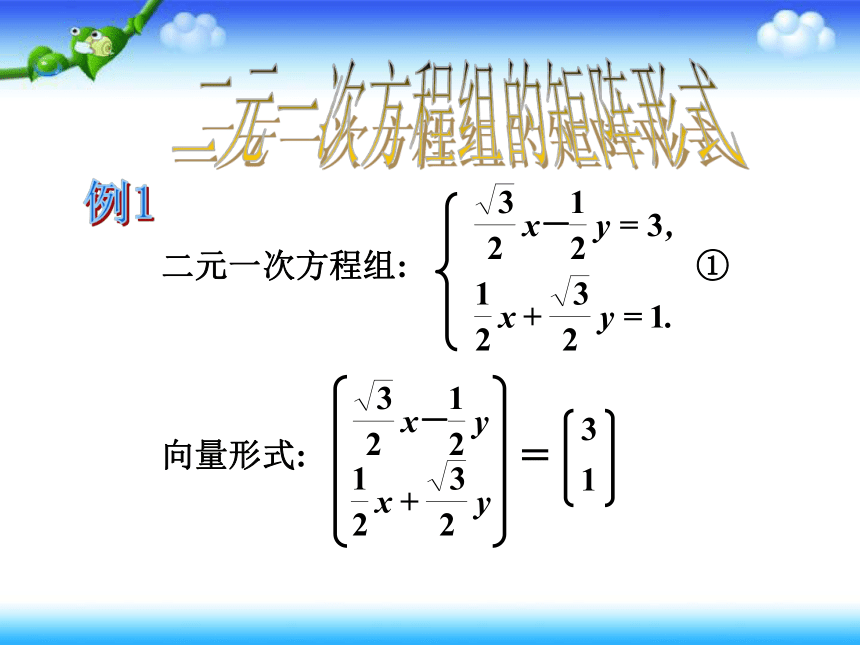
例1
向量形式:
二元一次方程组:
①
由矩阵与向量乘法的定义得:
∴原方程组①变成:
由例1→一般情况
关于变量x,y的二元一次方程组为:
则它可以写成矩阵的形式:
矩阵A= 称为二元一次方程组②
的系数矩阵. ③式称为二元一次方程组②的矩阵形式.
②
③
探究1
二元一次方程组的系数矩阵对应着一个线性变换,试从线性变换的角度揭示解二元一次方程组的意义.
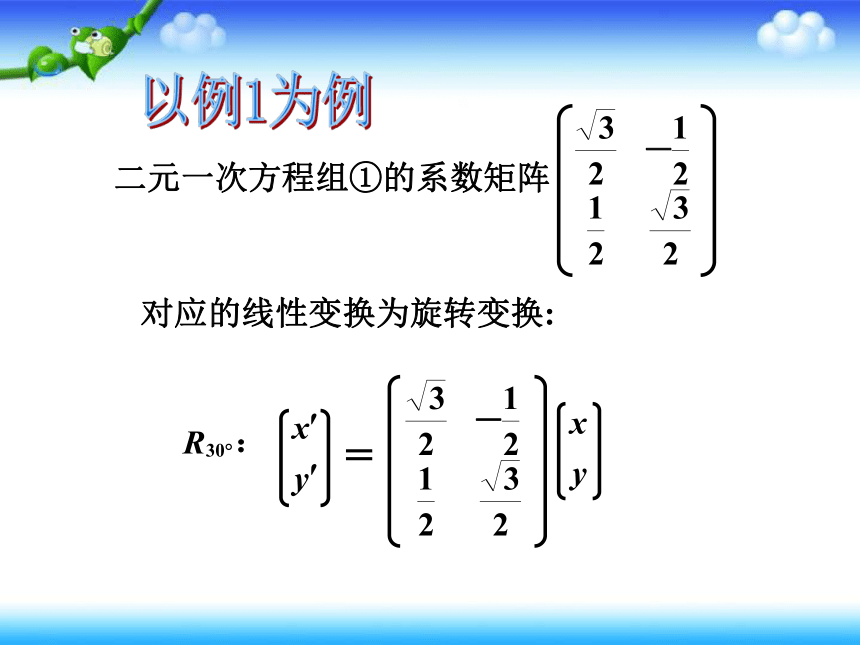
以例1为例
二元一次方程组①的系数矩阵
对应的线性变换为旋转变换:
∴解二元一次方程组①就是找到向量
使得它在该旋转变换下变为向量
举一反三
对于一般的二元一次方程组
②
以线性变换的角度看,可表述为:
线性变换
平面上一个确定的向量
已知:
要找到一个向量
使得它在ρ的作用下变为已知向量
注意
在实际操作中,若线性变换ρ的意
义不明显或不为我们所知,那么就很难
找到向量 , 使得
引入定义
二元一次方程组②的解写成向量
的形式,称这种形式的解为二元一次方程
组②的解向量.
逆矩阵与二元一次方程组
探究2
如果二元一次方程组的系数矩阵可逆,能用逆矩阵来解方程组么?
以例1为例
二元一次方程组①的系数矩阵
可逆
从线性变换的角度, 解方程组①就是找出向量
使得它在旋转变换
作用下的结果为给定的向量
即: 向量 按逆时针绕原点旋转30°
后得到向量 ;
向量 可以看成把向量 按
顺时针绕原点旋转30°后得到.
即:
∴二元一次方程组①一定有解,且解为:
∵二元一次方程组①的任意一个解向量都满足:
∴由几何上易看出:二元一次方程组①的解是唯一的.
定理
若关于变量x,y的二元一次方程组(线性
方程组): 的系数矩阵A=
可逆,则方程组有唯一解
-1
证明:
当A= 可逆,由二元一次方
程组 的矩阵形式:
A = 得:
A-1
A
=A-1
∴
E2 =
A-1
∴原方程组有解:
-1
下证唯一性:
设 , 是原方程组的任意两个解,由
上面的证明过程可得:
A-1
A-1
∴ = ,即二元一次方程组的
解是唯一的.
推论
关于变量x,y的二元一次方程组
其中a,b,c,d是不全为零的常数,有非零解的
充要条件是系数矩阵的行列式 =0.
注意:
常数项都为零的线性方程组为齐次线
性方程组, 是其中一个解,称为零解.
若向量 ( , 不全为零 )是该方程
组的解向量,则称之为一个非零解.
课堂练习
1.关于变量x,y的二元一次方程组
其中λ,μ为常数,求当λ和μ满足什么条件时,原方程组有非零解?
解:由推论可得:
当系数行列式 =0时,原方程
组由非零解.
即: 当2-λμ=0时,方程组有非零解.
∴λμ=2.
2.用逆矩阵解二元一次方程组
解:二元一次方程组的系数矩阵A=
则该方程组的矩阵形式:
∴系数矩阵A= 可逆
∴方程组有唯一解 =A-1
∵A-1= =
-1
∴
∴原方程组的解是
3.原方程组变形为:
它有非零解的充要条件是:
即:
再见
导入新课
在解析几何中,二元一次方程组的解的意义是什么?
直角坐标系x O y内相应的两条直线交点的坐标.
线性变换的表达式形式与二元一次方程组有很多相似的地方,能否从线性变换的角度来解释二元一次方程组的解的意义呢?
3.3 逆矩阵与二元一次方程组
二元一次方程组的矩阵形式
逆矩阵与二元一次方程组
学习重难点
用变换的观点认识解二元一次方程组的意义,会用系数矩阵的逆矩阵解系数矩阵可逆的二元一次方程组.
二元一次方程组的矩阵形式
例1
向量形式:
二元一次方程组:
①
由矩阵与向量乘法的定义得:
∴原方程组①变成:
由例1→一般情况
关于变量x,y的二元一次方程组为:
则它可以写成矩阵的形式:
矩阵A= 称为二元一次方程组②
的系数矩阵. ③式称为二元一次方程组②的矩阵形式.
②
③
探究1
二元一次方程组的系数矩阵对应着一个线性变换,试从线性变换的角度揭示解二元一次方程组的意义.
以例1为例
二元一次方程组①的系数矩阵
对应的线性变换为旋转变换:
∴解二元一次方程组①就是找到向量
使得它在该旋转变换下变为向量
举一反三
对于一般的二元一次方程组
②
以线性变换的角度看,可表述为:
线性变换
平面上一个确定的向量
已知:
要找到一个向量
使得它在ρ的作用下变为已知向量
注意
在实际操作中,若线性变换ρ的意
义不明显或不为我们所知,那么就很难
找到向量 , 使得
引入定义
二元一次方程组②的解写成向量
的形式,称这种形式的解为二元一次方程
组②的解向量.
逆矩阵与二元一次方程组
探究2
如果二元一次方程组的系数矩阵可逆,能用逆矩阵来解方程组么?
以例1为例
二元一次方程组①的系数矩阵
可逆
从线性变换的角度, 解方程组①就是找出向量
使得它在旋转变换
作用下的结果为给定的向量
即: 向量 按逆时针绕原点旋转30°
后得到向量 ;
向量 可以看成把向量 按
顺时针绕原点旋转30°后得到.
即:
∴二元一次方程组①一定有解,且解为:
∵二元一次方程组①的任意一个解向量都满足:
∴由几何上易看出:二元一次方程组①的解是唯一的.
定理
若关于变量x,y的二元一次方程组(线性
方程组): 的系数矩阵A=
可逆,则方程组有唯一解
-1
证明:
当A= 可逆,由二元一次方
程组 的矩阵形式:
A = 得:
A-1
A
=A-1
∴
E2 =
A-1
∴原方程组有解:
-1
下证唯一性:
设 , 是原方程组的任意两个解,由
上面的证明过程可得:
A-1
A-1
∴ = ,即二元一次方程组的
解是唯一的.
推论
关于变量x,y的二元一次方程组
其中a,b,c,d是不全为零的常数,有非零解的
充要条件是系数矩阵的行列式 =0.
注意:
常数项都为零的线性方程组为齐次线
性方程组, 是其中一个解,称为零解.
若向量 ( , 不全为零 )是该方程
组的解向量,则称之为一个非零解.
课堂练习
1.关于变量x,y的二元一次方程组
其中λ,μ为常数,求当λ和μ满足什么条件时,原方程组有非零解?
解:由推论可得:
当系数行列式 =0时,原方程
组由非零解.
即: 当2-λμ=0时,方程组有非零解.
∴λμ=2.
2.用逆矩阵解二元一次方程组
解:二元一次方程组的系数矩阵A=
则该方程组的矩阵形式:
∴系数矩阵A= 可逆
∴方程组有唯一解 =A-1
∵A-1= =
-1
∴
∴原方程组的解是
3.原方程组变形为:
它有非零解的充要条件是:
即:
再见
