人教A版高中数学选修4-2 第一讲 二 二阶矩阵与平面向量的乘法 上课课件(共18张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-2 第一讲 二 二阶矩阵与平面向量的乘法 上课课件(共18张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 420.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 21:15:22 | ||
图片预览





文档简介
(共18张PPT)
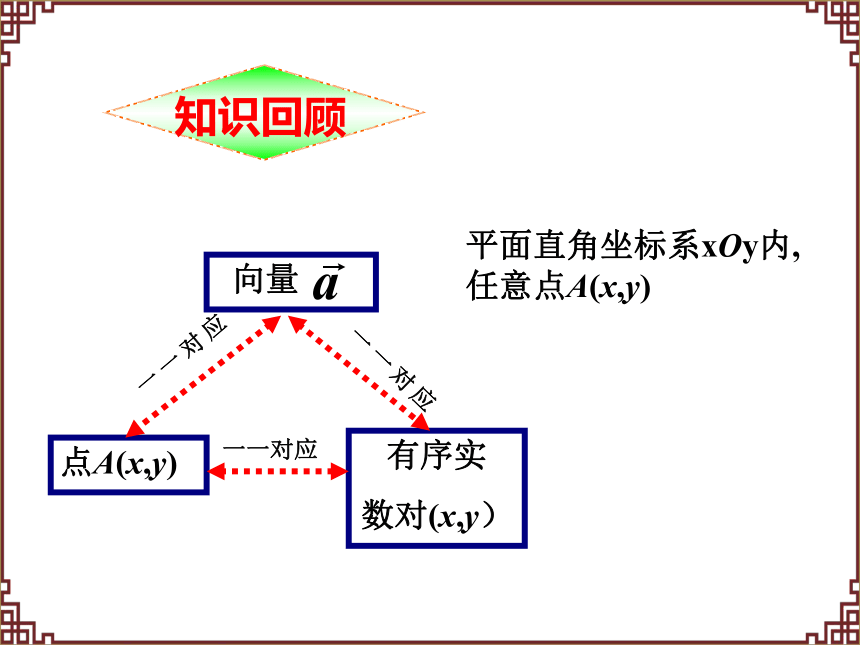
知识回顾
平面直角坐标系xOy内,任意点A(x,y)
点A(x,y)
有序实
数对(x,y)
向量
一一对应
应对一一
应对一一
通过上一节的学习,我们知道线性变换和二阶矩阵是一一对应的.那么能否用二阶矩阵表示线性变换呢?
新课导入
1.2 二阶矩阵与平面向量的乘法
教学目标
知识与能力
学会计算二阶矩阵与平面向量的乘积
过程与方法
情感态度和价值观
以变换的观点认识矩阵与向量乘法的意义.
培养学生的反向思维,进一步搞清二阶矩阵与线性变换之间的联系.
教学重难点
重点
二阶矩阵与平面向量的乘积.
难点
以变换的观点认识矩阵与向量乘法的意义.
向量(x,y)是 一对有序数组, x,y是它的两个分量.写成 这种形式的向量称为列向量.
规定:所有平面向量都写成列向量的形式.
引入定义
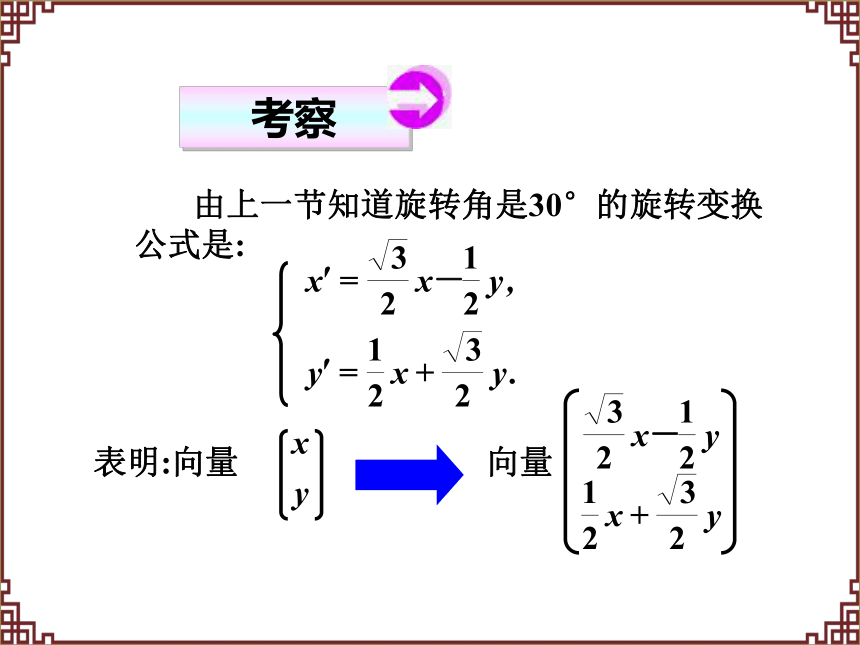
考察
由上一节知道旋转角是30°的旋转变换公式是:
表明:向量
向量
=
引入二阶矩阵与平面向量的乘法
则旋转角是30°的旋转变换的坐标变换公式写为:
=
∴二阶矩阵
=
所对应的旋转变换可写成:
设A= , = ,规定二阶矩阵
A与向量 的乘积为向量 ,记为A
或
定义
即:
A =
=
思考题的答案:
能用二阶矩阵表示线性变换
任何一个线性变换
都可表示成
=
实现了用二阶矩阵和平面向量的乘积来表示线性变换的目的.
课堂练习
=
=
解:A =
例1 设A= , = ,求A .
解:∵A =
=
例2 设矩阵A= ,求点
在A所对应的线性变换下的原像P’坐标.
解:设A= ,则
=
①
=
②
例3 设矩阵A对应的线性变换把点 变成点 ,把点 变成点 ,那么这个线性变化把点M(1,2)变成什么.
由①、②得
∴
∴A=
∴M’=
=
好棒噢
再见
知识回顾
平面直角坐标系xOy内,任意点A(x,y)
点A(x,y)
有序实
数对(x,y)
向量
一一对应
应对一一
应对一一
通过上一节的学习,我们知道线性变换和二阶矩阵是一一对应的.那么能否用二阶矩阵表示线性变换呢?
新课导入
1.2 二阶矩阵与平面向量的乘法
教学目标
知识与能力
学会计算二阶矩阵与平面向量的乘积
过程与方法
情感态度和价值观
以变换的观点认识矩阵与向量乘法的意义.
培养学生的反向思维,进一步搞清二阶矩阵与线性变换之间的联系.
教学重难点
重点
二阶矩阵与平面向量的乘积.
难点
以变换的观点认识矩阵与向量乘法的意义.
向量(x,y)是 一对有序数组, x,y是它的两个分量.写成 这种形式的向量称为列向量.
规定:所有平面向量都写成列向量的形式.
引入定义
考察
由上一节知道旋转角是30°的旋转变换公式是:
表明:向量
向量
=
引入二阶矩阵与平面向量的乘法
则旋转角是30°的旋转变换的坐标变换公式写为:
=
∴二阶矩阵
=
所对应的旋转变换可写成:
设A= , = ,规定二阶矩阵
A与向量 的乘积为向量 ,记为A
或
定义
即:
A =
=
思考题的答案:
能用二阶矩阵表示线性变换
任何一个线性变换
都可表示成
=
实现了用二阶矩阵和平面向量的乘积来表示线性变换的目的.
课堂练习
=
=
解:A =
例1 设A= , = ,求A .
解:∵A =
=
例2 设矩阵A= ,求点
在A所对应的线性变换下的原像P’坐标.
解:设A= ,则
=
①
=
②
例3 设矩阵A对应的线性变换把点 变成点 ,把点 变成点 ,那么这个线性变化把点M(1,2)变成什么.
由①、②得
∴
∴A=
∴M’=
=
好棒噢
再见
