人教A版高中数学选修4-2 第一讲 三 线性变换的基本性质 上课课件(共29张PPT)
文档属性
| 名称 | 人教A版高中数学选修4-2 第一讲 三 线性变换的基本性质 上课课件(共29张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 21:14:43 | ||
图片预览








文档简介
(共29张PPT)
新课导入
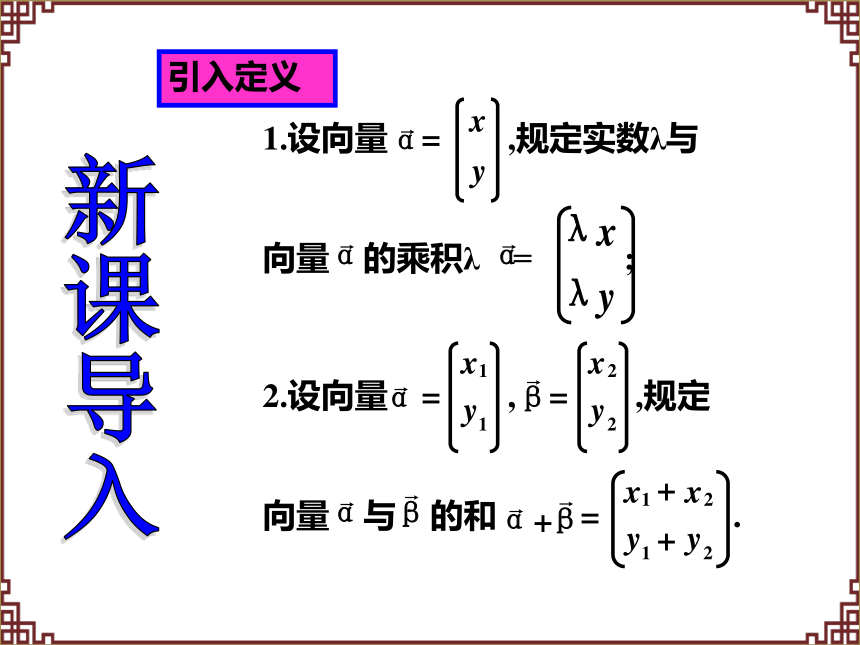
引入定义
1.设向量 = ,规定实数λ与
向量 的乘积λ = ;
2.设向量 = , = ,规定
向量 与 的和 = .
思考
作图说明数乘平面向量的几何意义?
作图说明平面向量加法的几何意义?
1.3 线性变换的基本性质
线性变换的基本性质
一些重要的线性变换对单位正方形区域的作用
教学目标
知识与能力
过程与方法
情感态度和价值观
通过大量具体的矩阵对平面上给定图形的(如正方形)的变换,认识到矩阵可表示如下的线性变换:恒等、反射、伸压、旋转、切变、投影
加深学生对线性变换及其基本性质理解
教学重难点
线性变换的基本性质及其几何意义
矩阵对几种特殊线性变换的表示
重点
难点
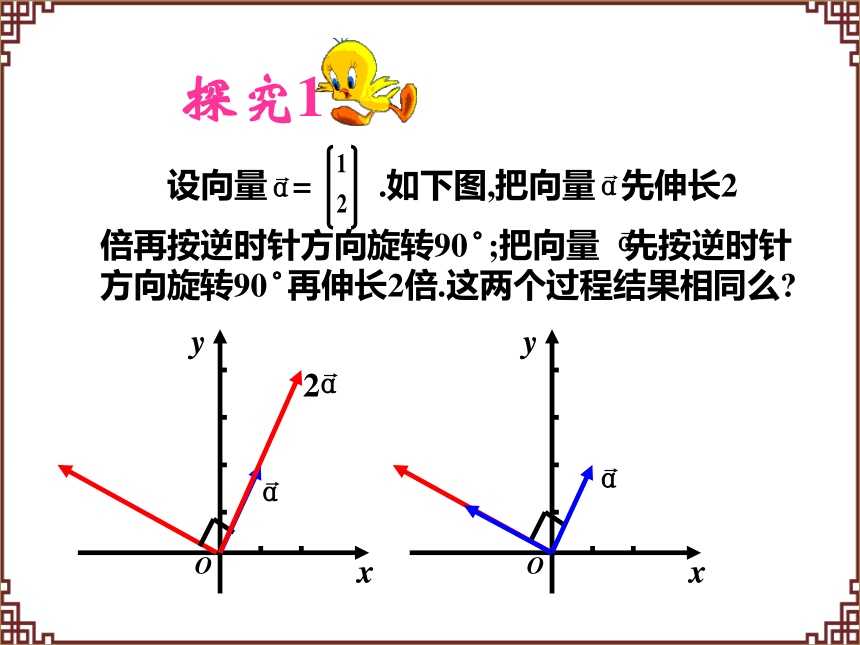
探究1
O
y
x
O
y
x
设向量 = .如下图,把向量 先伸长2
倍再按逆时针方向旋转90°;把向量 先按逆时针方向旋转90°再伸长2倍.这两个过程结果相同么?
∵这个旋转变换的矩阵为A=
∵2 =
∴A(2 )=
=
2A =2
=
∴A(2 )=2A .
举一反三
请同学们自己验证!
一般地,设A是一个二阶矩阵, 是平面上的任意一个向量,λ是任意实数,则A(λ )=λA .
探究2
设向量 = , = .如图,先利用平
面四边形法则求 ,再对向量( )进行关于x轴的反射变换;或者,先对向量 , 做关于x轴的反射变换,再利用平行四边形法则求反射变换的两个向量的和.这两个过程的结果相同么?
O
y
x
O
y
x
关于x轴的反射变换的矩阵A= .
∵ =
∴A( )= A +A
=
A +A =
+
∴A( )=
=
举一反三
请同学们自己验证!
一般地,设A是一个二阶矩阵, , 是平面上的任两个向量,A( )= A +A .
性质1
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ是任意实数,则
(1) A(λ )=λA ;
(2) A( )= A +A .
定理1
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ1,λ2是任意实数,
则A(λ1 + λ2 )= λ1 A + λ2 A .
证明:由性质1得
A(λ1 + λ2 )= A(λ1 )+ A(λ2 )
=λ1 A + λ2 A .
探究3
旋转变换R30°: =
把直线y=kx+b(其中k,b均为常数)变成了什么图形?
答案:直线
探究4
切变变换:σ: =
把直线 (其中k,b均为常数)变成了什么图形?
答案:点( ,0 )
∵
∴
∵
∴
性质2
二阶矩阵对应的线性变换把平面上的直线变成直线(或一点).
y
O
x
P2
P
P1
由定理1,直线l在线性变换
=A 的作用下变成
(其中λ1,λ2是实数,且λ1 +λ2=1)
重要线性变换对单位正方形区域的作用
1.恒等变换
【平面图形(单位正方形)在线性变换的作用下会变成什么图形?】
定义: 把平面上任意一点变成它本身的变换.
恒等变换I 对应的矩阵为E2=
变换公式:
∵E2 = = ,
E2 = = .
O
y
x
1
1
O
y
x
1
1
解这类题型的一般步骤:
1.写出变换所对应的矩阵A;
2.写出坐标变换公式;
3.求出A ,A ,即得到单位正方形区域两条邻边的新位置.作图表示
总结
请同学们练习以下情况
1.旋转变换R30°
2. 切变变换(平行与x轴、y轴)
3.反射变换( 关于x轴、y轴)
4.投影变换( 关于x轴、y轴)
关于x轴的切变变换所对应的矩阵为A=
k为非零常数,随着k 的变化,所对应的图形也变化.
注意
课堂练习
1.旋转变换R30°所对应的矩阵
2.旋转变换R45°所对应的矩阵
O
y
x
1
1
3.平行于x轴的切变变换,对应的矩阵
为A= ,作图表示变化后的图形.
1
1
y
x
O
课堂小结
1.线性变换的基本性质:
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ是任意实数,则
(1) A(λ )=λA ;
(2) A( )= A +A .
二阶矩阵对应的线性变换把平面上的直线变成直线(或一点).
重要的线性变换
恒等变换
旋转变换
切变变换
反射变换
投影变换
单位正方形在这些变换作用下所变成的图形.
再见
新课导入
引入定义
1.设向量 = ,规定实数λ与
向量 的乘积λ = ;
2.设向量 = , = ,规定
向量 与 的和 = .
思考
作图说明数乘平面向量的几何意义?
作图说明平面向量加法的几何意义?
1.3 线性变换的基本性质
线性变换的基本性质
一些重要的线性变换对单位正方形区域的作用
教学目标
知识与能力
过程与方法
情感态度和价值观
通过大量具体的矩阵对平面上给定图形的(如正方形)的变换,认识到矩阵可表示如下的线性变换:恒等、反射、伸压、旋转、切变、投影
加深学生对线性变换及其基本性质理解
教学重难点
线性变换的基本性质及其几何意义
矩阵对几种特殊线性变换的表示
重点
难点
探究1
O
y
x
O
y
x
设向量 = .如下图,把向量 先伸长2
倍再按逆时针方向旋转90°;把向量 先按逆时针方向旋转90°再伸长2倍.这两个过程结果相同么?
∵这个旋转变换的矩阵为A=
∵2 =
∴A(2 )=
=
2A =2
=
∴A(2 )=2A .
举一反三
请同学们自己验证!
一般地,设A是一个二阶矩阵, 是平面上的任意一个向量,λ是任意实数,则A(λ )=λA .
探究2
设向量 = , = .如图,先利用平
面四边形法则求 ,再对向量( )进行关于x轴的反射变换;或者,先对向量 , 做关于x轴的反射变换,再利用平行四边形法则求反射变换的两个向量的和.这两个过程的结果相同么?
O
y
x
O
y
x
关于x轴的反射变换的矩阵A= .
∵ =
∴A( )= A +A
=
A +A =
+
∴A( )=
=
举一反三
请同学们自己验证!
一般地,设A是一个二阶矩阵, , 是平面上的任两个向量,A( )= A +A .
性质1
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ是任意实数,则
(1) A(λ )=λA ;
(2) A( )= A +A .
定理1
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ1,λ2是任意实数,
则A(λ1 + λ2 )= λ1 A + λ2 A .
证明:由性质1得
A(λ1 + λ2 )= A(λ1 )+ A(λ2 )
=λ1 A + λ2 A .
探究3
旋转变换R30°: =
把直线y=kx+b(其中k,b均为常数)变成了什么图形?
答案:直线
探究4
切变变换:σ: =
把直线 (其中k,b均为常数)变成了什么图形?
答案:点( ,0 )
∵
∴
∵
∴
性质2
二阶矩阵对应的线性变换把平面上的直线变成直线(或一点).
y
O
x
P2
P
P1
由定理1,直线l在线性变换
=A 的作用下变成
(其中λ1,λ2是实数,且λ1 +λ2=1)
重要线性变换对单位正方形区域的作用
1.恒等变换
【平面图形(单位正方形)在线性变换的作用下会变成什么图形?】
定义: 把平面上任意一点变成它本身的变换.
恒等变换I 对应的矩阵为E2=
变换公式:
∵E2 = = ,
E2 = = .
O
y
x
1
1
O
y
x
1
1
解这类题型的一般步骤:
1.写出变换所对应的矩阵A;
2.写出坐标变换公式;
3.求出A ,A ,即得到单位正方形区域两条邻边的新位置.作图表示
总结
请同学们练习以下情况
1.旋转变换R30°
2. 切变变换(平行与x轴、y轴)
3.反射变换( 关于x轴、y轴)
4.投影变换( 关于x轴、y轴)
关于x轴的切变变换所对应的矩阵为A=
k为非零常数,随着k 的变化,所对应的图形也变化.
注意
课堂练习
1.旋转变换R30°所对应的矩阵
2.旋转变换R45°所对应的矩阵
O
y
x
1
1
3.平行于x轴的切变变换,对应的矩阵
为A= ,作图表示变化后的图形.
1
1
y
x
O
课堂小结
1.线性变换的基本性质:
设A是一个二阶矩阵, , 是平面上的任意两个向量,λ是任意实数,则
(1) A(λ )=λA ;
(2) A( )= A +A .
二阶矩阵对应的线性变换把平面上的直线变成直线(或一点).
重要的线性变换
恒等变换
旋转变换
切变变换
反射变换
投影变换
单位正方形在这些变换作用下所变成的图形.
再见
