人教版数学八年级下册18.1.1 平行四边形的对角线的特征课件(第2课时 17张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.1 平行四边形的对角线的特征课件(第2课时 17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 249.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 11:39:02 | ||
图片预览


文档简介
(共17张PPT)
导入新课
18.1.1 平行四边形的性质
第2课时 平行四边形的对角线的特征
第十八章 平行四边形
讲授新课
当堂练习
课堂小结
学习目标
1.探索并掌握平行四边形对角线性质;
2.灵活运用平行四边形的性质进行推理和计算.
学习重点:平行四边形对角线互相平分的性质,以及性质的应用.
学习难点:综合运用平行四边形的性质进行有关的论证和计算.
评一评
导入新课
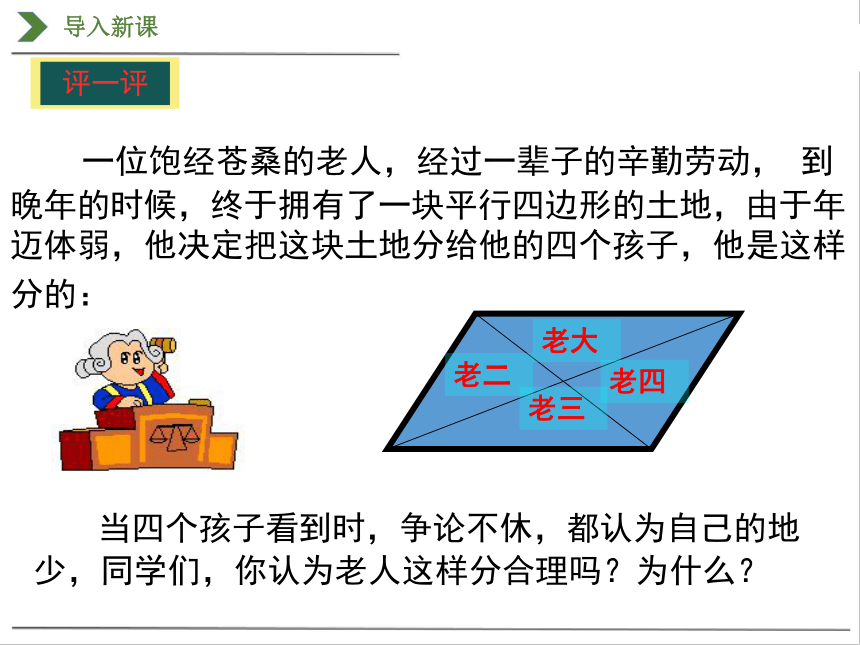
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
讲授新课
平行四边形的对角线的性质
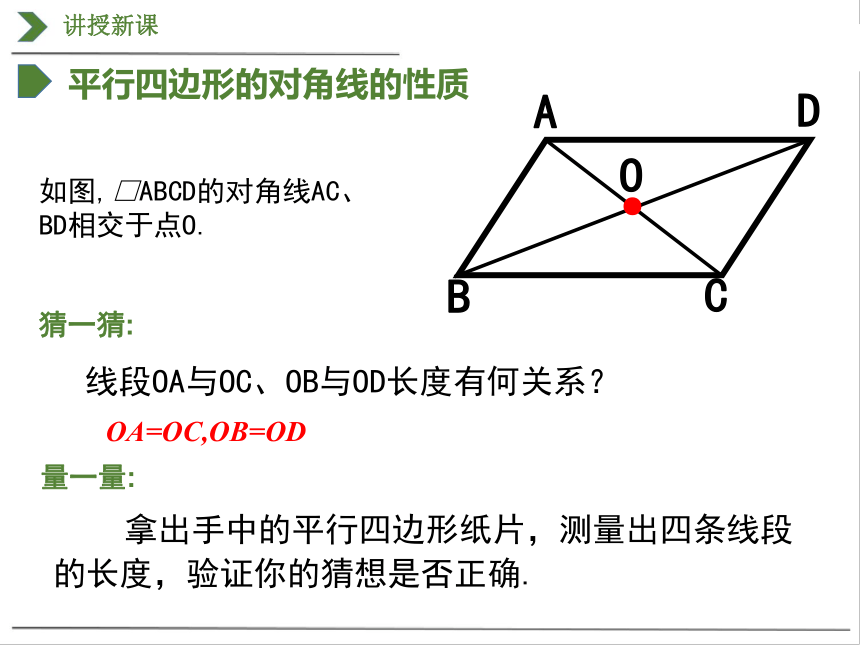
如图,□ABCD的对角线AC、BD相交于点O.
猜一猜:
线段OA与OC、OB与OD长度有何关系?
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
A
C
D
B
O
●
OA=OC,OB=OD
●
A
D
O
C
B
D
B
O
C
A
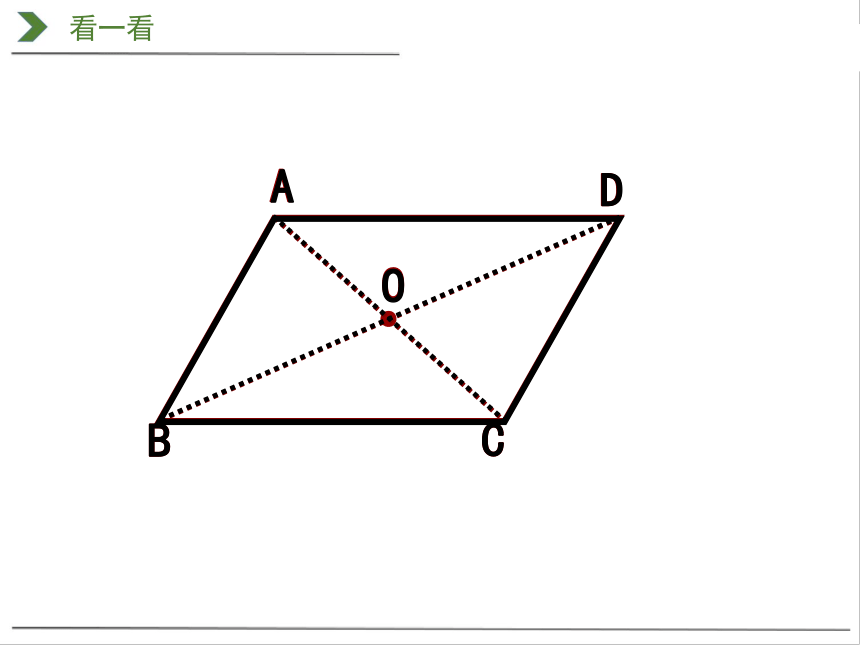
看一看
证一证
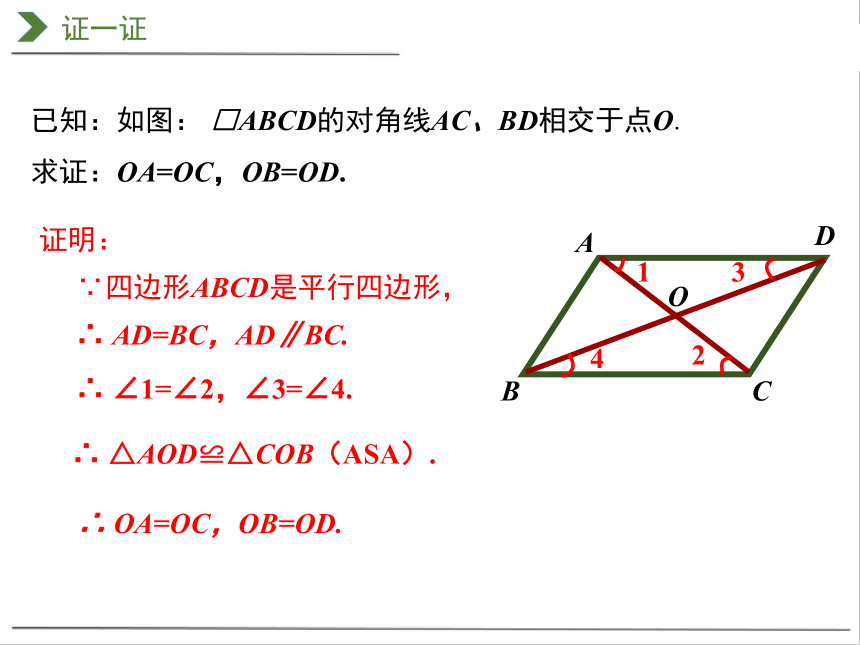
已知:如图: □ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
A
C
D
B
O
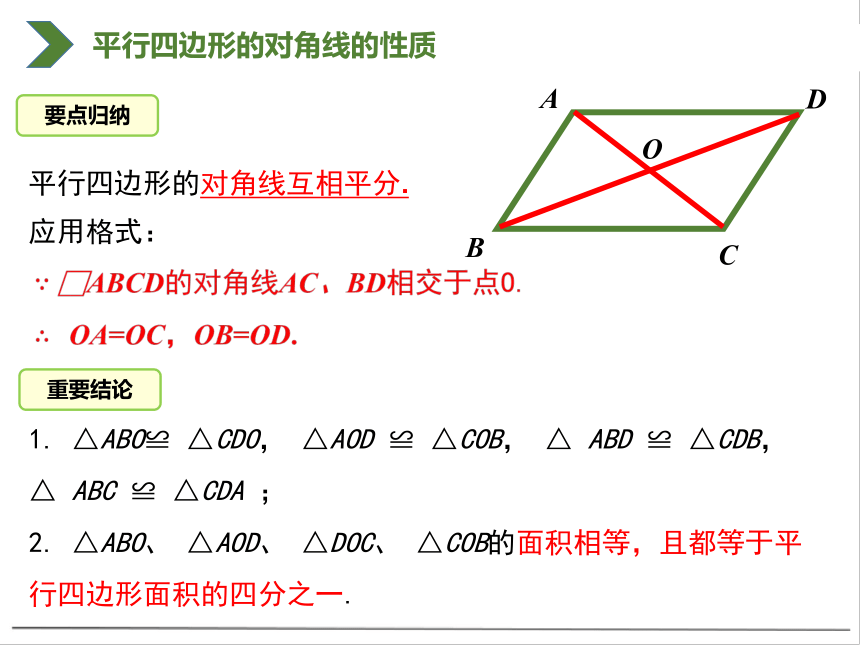
平行四边形的对角线互相平分.
要点归纳
重要结论
应用格式:
?
平行四边形的对角线的性质
1. △ABO≌ △CDO, △AOD ≌ △COB, △ ABD ≌ △CDB, △ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
例1 如图,在□ABCD中,BC=10cm, AC=8cm,BD=14cm
(1)△ BOC的周长是多少?
说明理由?
10+4+7=21
( 2) △ ABC与△ DBC的周长哪个长,长多少?
△ ABC的周长小于△ DBC的周长
小6
B
C
D
A
O
典例精析
?
39
?
8
B
C
D
A
O
变式3 在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是 .
A. 24C.7C
?
A
B
C
D
O
解;∵四边形ABCD是平行四边形
根据勾股定理,
∴BC=AD=8,CD=AB=10.
是直角三角形.
又OA=OC,
老人分地合理吗?
老大
老二
老三
老四
评一评
答:老人分地合理.由前面可知,老大与老三,老二与老四的(三角形)地全等.老大与老二的(三角形)地面积相等,因为三角形的中线把原三角形分成面积相等的两部分.
当堂练习
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
2.如图, □ABCD的对角线AC、BD相交于点O,且AC+BD=16,
CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
B
C
D
A
O
4、平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm
C、4cm和8cm D、10㎝和2 ㎝
3、在□ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
D
C
解答:
如图,过点C作CF∥BD,交AB延长线于点F,
∴四边形BFCD为平行四边形,
∴CF=BD,
∴在△AFC中:AC?CF∵AB=5,
∴选项中只有C中的数据能满足此关系:8?4=4<5×2<8+4=12,
故选C.
考点:[平行四边形的性质, 三角形三边关系]
分析:作辅助线,再根据三角形的三边关系求出两条对角线的长.
5.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .
10
A
B
C
D
E
F
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是 .
□
7.如图,平行四边形ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F.
求证:OE=OF
●
O
F
A
B
C
D
E
●
●
3
4
2
1
3
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
两条对角线互相平分.
课后作业
导入新课
18.1.1 平行四边形的性质
第2课时 平行四边形的对角线的特征
第十八章 平行四边形
讲授新课
当堂练习
课堂小结
学习目标
1.探索并掌握平行四边形对角线性质;
2.灵活运用平行四边形的性质进行推理和计算.
学习重点:平行四边形对角线互相平分的性质,以及性质的应用.
学习难点:综合运用平行四边形的性质进行有关的论证和计算.
评一评
导入新课
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
讲授新课
平行四边形的对角线的性质
如图,□ABCD的对角线AC、BD相交于点O.
猜一猜:
线段OA与OC、OB与OD长度有何关系?
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
A
C
D
B
O
●
OA=OC,OB=OD
●
A
D
O
C
B
D
B
O
C
A
看一看
证一证
已知:如图: □ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
A
C
D
B
O
平行四边形的对角线互相平分.
要点归纳
重要结论
应用格式:
?
平行四边形的对角线的性质
1. △ABO≌ △CDO, △AOD ≌ △COB, △ ABD ≌ △CDB, △ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
例1 如图,在□ABCD中,BC=10cm, AC=8cm,BD=14cm
(1)△ BOC的周长是多少?
说明理由?
10+4+7=21
( 2) △ ABC与△ DBC的周长哪个长,长多少?
△ ABC的周长小于△ DBC的周长
小6
B
C
D
A
O
典例精析
?
39
?
8
B
C
D
A
O
变式3 在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是 .
A. 24
?
A
B
C
D
O
解;∵四边形ABCD是平行四边形
根据勾股定理,
∴BC=AD=8,CD=AB=10.
是直角三角形.
又OA=OC,
老人分地合理吗?
老大
老二
老三
老四
评一评
答:老人分地合理.由前面可知,老大与老三,老二与老四的(三角形)地全等.老大与老二的(三角形)地面积相等,因为三角形的中线把原三角形分成面积相等的两部分.
当堂练习
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
2.如图, □ABCD的对角线AC、BD相交于点O,且AC+BD=16,
CD=6,则△ABO的周长是( )
A. 10 B. 14 C. 20 D. 22
B
B
C
D
A
O
4、平行四边形的一边长为5cm,则它的对角线可能是( )
A、4cm和6cm B、4cm和14cm
C、4cm和8cm D、10㎝和2 ㎝
3、在□ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
D
C
解答:
如图,过点C作CF∥BD,交AB延长线于点F,
∴四边形BFCD为平行四边形,
∴CF=BD,
∴在△AFC中:AC?CF
∴选项中只有C中的数据能满足此关系:8?4=4<5×2<8+4=12,
故选C.
考点:[平行四边形的性质, 三角形三边关系]
分析:作辅助线,再根据三角形的三边关系求出两条对角线的长.
5.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .
10
A
B
C
D
E
F
6.如图,平行四边形ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,则BD的长是 .
□
7.如图,平行四边形ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F.
求证:OE=OF
●
O
F
A
B
C
D
E
●
●
3
4
2
1
3
课堂小结
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
两条对角线互相平分.
课后作业
