人教版初中数学七年级下册9.1.2.1不等式的性质1课件(共22张PPT)
文档属性
| 名称 | 人教版初中数学七年级下册9.1.2.1不等式的性质1课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 11:44:31 | ||
图片预览







文档简介
(共22张PPT)
9.1.2 不等式的性质
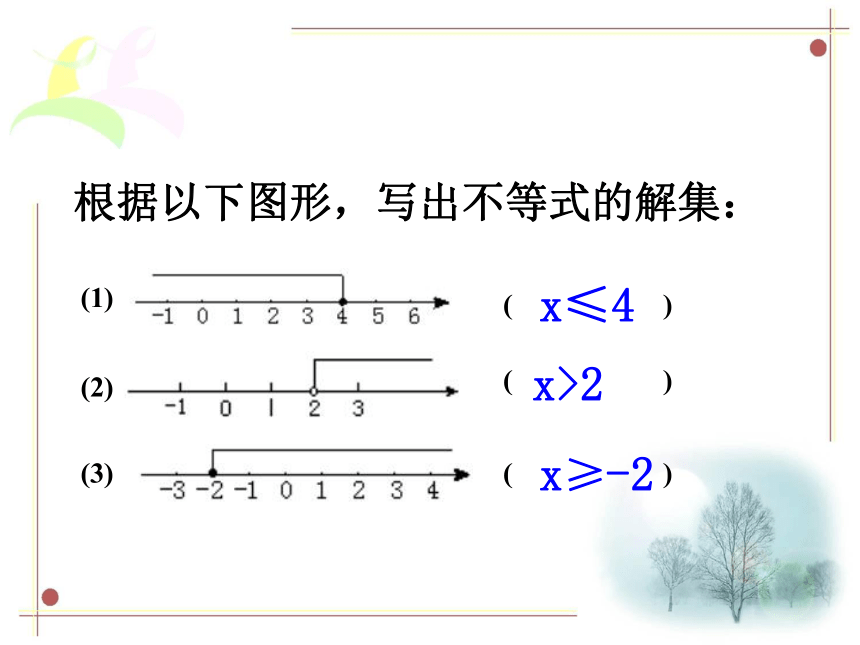
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
大于向右,小于向左,有等号为实心,无等号为空心.
规律:
(1)x≤-1 (2)x≥-3
(3)x<2 (4)-3≤x<2
在数轴上表示下列不等式的解集:
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
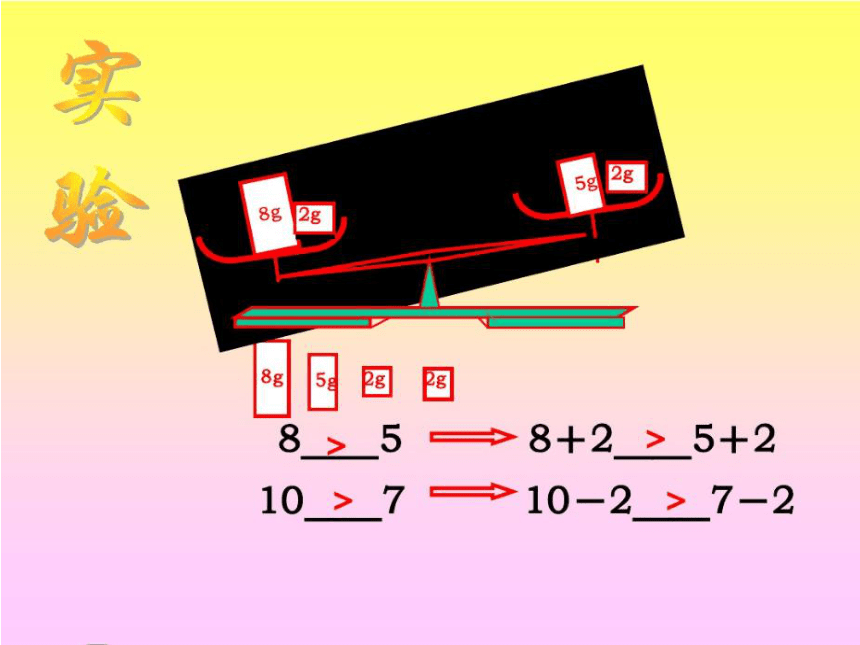
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)____3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
发现:同乘以一个正数,不等号方向不变,同乘以一个 负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
猜想2:不等式两边都乘以(或除以)同一个不为零的数,不等号
的方向是否改变?
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
举例分析:
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
我是最棒的
?
做一做:
选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
试一试
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
解:(1) x-2+2<3+2
x<5
(2) 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列不等式化成
x<a 或x>a的形式:
x-2< 3 (2) 6x< 5x-1
试一试
尝试探索
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
巩固新知
再见
9.1.2 不等式的性质
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
大于向右,小于向左,有等号为实心,无等号为空心.
规律:
(1)x≤-1 (2)x≥-3
(3)x<2 (4)-3≤x<2
在数轴上表示下列不等式的解集:
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)____3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
发现:同乘以一个正数,不等号方向不变,同乘以一个 负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
猜想2:不等式两边都乘以(或除以)同一个不为零的数,不等号
的方向是否改变?
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
举例分析:
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
例1:
?判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
我是最棒的
?
做一做:
选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
试一试
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
解:(1) x-2+2<3+2
x<5
(2) 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列不等式化成
x<a 或x>a的形式:
x-2< 3 (2) 6x< 5x-1
试一试
尝试探索
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
巩固新知
再见
