青岛版数学八下第10章一次函数综合复习课件(共36张PPT)
文档属性
| 名称 | 青岛版数学八下第10章一次函数综合复习课件(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:24:39 | ||
图片预览











文档简介
(共36张PPT)
数学
讲次名称:一次函数综合
一次函数的代数综合
模块名称
方法展示
用函数观点看方程(组)
答 案
【示例】 求y=2x+3与x轴交点
分析:令y= 则2x+3= 所以x= .
发现:函数y=2x+3与x轴的交点横坐标与2x+3=0的解 .
0
0
相等
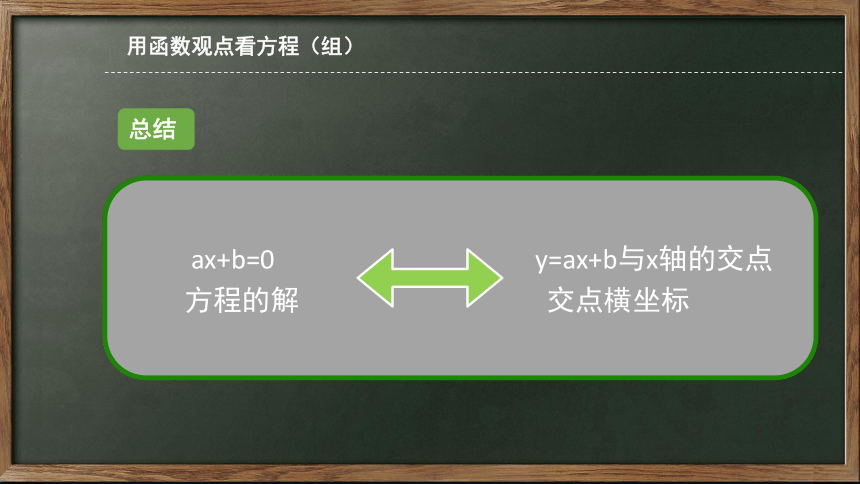
用函数观点看方程(组)
ax+b=0 y=ax+b与x轴的交点
方程的解 交点横坐标
总结
例1
答 案
直线y=3x+b与x轴的交点坐标是(1,0),则关于x的一元一次方程3x+b=0的解是 .
x=1
练习1.1
答 案
如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的方程kx+b=0的解为 .
x=-4
例2
答 案
(1)已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x= .
-2
例2
答 案
(2)如图,已知函数y=ax+b和y=kx的图象交于点p,则根据图象可得关于x的一元一次方程ax+b=kx的解为x= .
-4
练习2.1
答 案
已知,如图,直线l1:y1=a1x-b1与直线l2:y2=a2x-b2相交于点P(-1,2),则方程a1x-b1=a2x-b2的解为x= .
-1
方法展示
(1)根据图象可知,当y=0时,x=5;
(2)在图象上描出y>0时的部分,发现在x轴的 ,
∴x的取值范围为 .
(3)在图象上描出y<0时的部分,发现在x轴的 ,
∴x的取值范围为 .
用函数观点看不等
答 案
【示例】 如图,直线y=mx+n与x轴相交于点(5,0),
求:(1)当y=0时,x的取值;
(2)当y>0时,x的取值范围;
(3)当y<0时,x的取值范围;
上方
思路点拨
x<5
下方
x>5
找交点,描图象,定范围.
总 结
用函数观点看不等
例3
答 案
如图,一次函数y=kx+b的图象与x轴交于一点,则当y>0时,x的取值范围是( )
A. x<-2
B. x>-2
C. x>0
D. x<0
A
练习3.1
答 案
如图,一次函数y=kx+b(k为常数,k≠0)的图象与x轴交于点(2,0),则使y<0成立的x的取值范围是 .
x>2
例4
答 案
直线l1:y=k1x+b与直线l2:y=k2x+c在同一直角坐标系中的图象如图所示,则k1x+b<k2x+c时,x的取值范围是( )
A. x>1
B. x<1
C. x>-2
D. x<-2
B
练习4.1
答 案
如图,已知一次函数y1=-x+b的图象与y轴交于点(0,4),y2=kx-2的图象与x轴交于点B(1,0),那么使y1>y2成立的自变量x的取值范围是 .
x<2
练习4.1
解:将点A(0,4)带入一次函数y1=-x+b,
得:0+b=4,解得:b=4,
故函数解析式为y1=-x+4;
将点B(1,0)代入y2=kx-2,
得:k-2=0,解得:k=2,
故函数解析式为y2=2x-2,
再将y1=-x+4和y2=2x-2组成方程组
y=-x+4,解得: x=2
y=2x-2 y=2,
故两直线的交点为(2,2),
由图可知,当y1>y2时,x取交点左边的值,即x<2.
解析
一次函数的几何综合
模块名称
方法展示
【示例】如图,已知直线y=-2x+2与y轴交于点A,B是直线上一点,且S△AOB=2,求B点的坐标.
解:在直线上,任意取一点B,过点B作BC垂直y轴于点C,在△AOB,底: ,高 ,交点 .
S△AOB= × =2 ,得出BC= .
将 =2代入直线求B ,
注意:B点可以在y轴左侧
将x= 代入直线求B‘ .
一次函数与三角形面积
答 案
已知面积、解析式要大胆画图,注意会有多个解.
总结
答 案
OA
BC
A(0,2)
OA
BC
2
x
(2,-2)
-2
(-2,6)
②直线y=k2x+b2经过一、二、四象限,
∵S△AOB:S△BOC=1:2,A(3,1),
∴C(0,2)
∴ 2=b2 k2=
1=3k2+b2 b2=2
∴y= x+2
例5
答 案
在平面直角坐标系xOy中,直线y=kx+b经过点A(3,1),与x轴交于点B,与y轴交于点C,连接OA.若
S△AOB:S△BOC=1:2,求直线y=kx+b的解析式.
y=x-2或y= x+2
解析
①直线y=k1x+b1经过一、三、四象限,
∵S△AOB:S△BOC=1:2,A(3,1),
∴C(0,-2)
∴ -2=b1 k1=1
1=3k1+b1 b1=-2
∴y=x-2
练习5.1
答 案
如果一次函数y=kx+4与两坐标轴围成的三角形面积为4,则k= .
±2
解析
令y=0,x=
∴
k=±2.
方法展示
【示例】点P为x轴上一点,求CP+DP
最小时P的坐标.
解:点D作x轴对称点E,连接CE,
交x轴于点P,此时CP+DP最小. “将军饮马”问题
将C(-4,3),E(0,-3)代入y=kx+b;
解得 . 待定系数求CE解析式
点P在x轴上,令: -3=0得x= ;
∴P( , ) 求P坐标
一次函数中的“将军饮马”
答 案
-2
-2 0
数形结合,作出相应的辅助线,结合平面直角坐标系表示出相应的点坐标与数量关系
总结
一次函数中的“将军饮马”
例6
答 案
直线y= 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,请你在所给的坐标系中准确地画出点P的位置,并求出PC+PD值最小时点P的坐标.
P( ,0)
例6
解析
令y= 中,x=0,则y=4,
∴B( 0,4),
令y=0,则x=-6,
∴A(-6,0)
∵C、D分别为线段AB、OB的中点,
∴C(-3,2),D(0,2),
作D关于x轴对称点D',
∴D’(0,-2),
设直线CD‘解析式y=kx+b,
∴ 2=-3k+b k=
-2=b b=-2
∴y= x-2,
令y=0,则x=
∴P( ,0)
练习6.1
答 案
已知点A(0,2)、B(4,1),点P是x轴上的一点,则PA+PB的最小值是 .
5
作点A关于x轴的对称点A',连接A’B交x轴于点P,则P即为所求点.
∵点A(0,2)
∴点A关于x轴的对称点A‘的坐标为(0,-2),
∵A’(0,-2),B(4,1),
∴A‘B=
即PA+PB的最小值为5.
故答案为5.
解析
知识解读
一次函数与特殊三角形综合
引入
已知边AB,如何在坐标轴上找一点C,使得△ABC为等腰三角形?
两圆一线:
①若∠A为顶角.则点C在以 为圆心,以线段 为半径的小圆上;
②若∠B为顶角.则点C在以 为圆心,以线段 为半径的小圆上;
③若∠C为顶角.则点C在线段 的垂直平分线上;
一次函数与特殊三角形综合
答 案
A
讲解
AB
B
AB
AB
如图,在平面直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标
例7
解:(1)将点A(2,0)代入直线y=kx+3,
得0=2k+3,解得k= ,∴y= x+3.
当x=0时,y=3.∴B(0,3),OB=3.
当y=0时, x+3=0,∴x=2,
∴A(2,0),OA=2,
∴S△AOB= OA.OB= ×2×3=3.
(2)如图,符合条件的点C的坐标是
(-2,0)或( +2,0)或(2- ,0);
例7
答 案
练习7.1
答 案
已知一次函数y= x+1与x轴、y轴分别交于A、B两点,点P是坐标轴上的点,是否存在点P使得△ABP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
存在,(-2- ,0)、(0,-1)、(2- ,0)、(0,3)、( ,0)、(- ,0).
Thank you
数学
讲次名称:一次函数综合
一次函数的代数综合
模块名称
方法展示
用函数观点看方程(组)
答 案
【示例】 求y=2x+3与x轴交点
分析:令y= 则2x+3= 所以x= .
发现:函数y=2x+3与x轴的交点横坐标与2x+3=0的解 .
0
0
相等
用函数观点看方程(组)
ax+b=0 y=ax+b与x轴的交点
方程的解 交点横坐标
总结
例1
答 案
直线y=3x+b与x轴的交点坐标是(1,0),则关于x的一元一次方程3x+b=0的解是 .
x=1
练习1.1
答 案
如图,直线y=kx+b(k≠0)与x轴交于点(-4,0),则关于x的方程kx+b=0的解为 .
x=-4
例2
答 案
(1)已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x= .
-2
例2
答 案
(2)如图,已知函数y=ax+b和y=kx的图象交于点p,则根据图象可得关于x的一元一次方程ax+b=kx的解为x= .
-4
练习2.1
答 案
已知,如图,直线l1:y1=a1x-b1与直线l2:y2=a2x-b2相交于点P(-1,2),则方程a1x-b1=a2x-b2的解为x= .
-1
方法展示
(1)根据图象可知,当y=0时,x=5;
(2)在图象上描出y>0时的部分,发现在x轴的 ,
∴x的取值范围为 .
(3)在图象上描出y<0时的部分,发现在x轴的 ,
∴x的取值范围为 .
用函数观点看不等
答 案
【示例】 如图,直线y=mx+n与x轴相交于点(5,0),
求:(1)当y=0时,x的取值;
(2)当y>0时,x的取值范围;
(3)当y<0时,x的取值范围;
上方
思路点拨
x<5
下方
x>5
找交点,描图象,定范围.
总 结
用函数观点看不等
例3
答 案
如图,一次函数y=kx+b的图象与x轴交于一点,则当y>0时,x的取值范围是( )
A. x<-2
B. x>-2
C. x>0
D. x<0
A
练习3.1
答 案
如图,一次函数y=kx+b(k为常数,k≠0)的图象与x轴交于点(2,0),则使y<0成立的x的取值范围是 .
x>2
例4
答 案
直线l1:y=k1x+b与直线l2:y=k2x+c在同一直角坐标系中的图象如图所示,则k1x+b<k2x+c时,x的取值范围是( )
A. x>1
B. x<1
C. x>-2
D. x<-2
B
练习4.1
答 案
如图,已知一次函数y1=-x+b的图象与y轴交于点(0,4),y2=kx-2的图象与x轴交于点B(1,0),那么使y1>y2成立的自变量x的取值范围是 .
x<2
练习4.1
解:将点A(0,4)带入一次函数y1=-x+b,
得:0+b=4,解得:b=4,
故函数解析式为y1=-x+4;
将点B(1,0)代入y2=kx-2,
得:k-2=0,解得:k=2,
故函数解析式为y2=2x-2,
再将y1=-x+4和y2=2x-2组成方程组
y=-x+4,解得: x=2
y=2x-2 y=2,
故两直线的交点为(2,2),
由图可知,当y1>y2时,x取交点左边的值,即x<2.
解析
一次函数的几何综合
模块名称
方法展示
【示例】如图,已知直线y=-2x+2与y轴交于点A,B是直线上一点,且S△AOB=2,求B点的坐标.
解:在直线上,任意取一点B,过点B作BC垂直y轴于点C,在△AOB,底: ,高 ,交点 .
S△AOB= × =2 ,得出BC= .
将 =2代入直线求B ,
注意:B点可以在y轴左侧
将x= 代入直线求B‘ .
一次函数与三角形面积
答 案
已知面积、解析式要大胆画图,注意会有多个解.
总结
答 案
OA
BC
A(0,2)
OA
BC
2
x
(2,-2)
-2
(-2,6)
②直线y=k2x+b2经过一、二、四象限,
∵S△AOB:S△BOC=1:2,A(3,1),
∴C(0,2)
∴ 2=b2 k2=
1=3k2+b2 b2=2
∴y= x+2
例5
答 案
在平面直角坐标系xOy中,直线y=kx+b经过点A(3,1),与x轴交于点B,与y轴交于点C,连接OA.若
S△AOB:S△BOC=1:2,求直线y=kx+b的解析式.
y=x-2或y= x+2
解析
①直线y=k1x+b1经过一、三、四象限,
∵S△AOB:S△BOC=1:2,A(3,1),
∴C(0,-2)
∴ -2=b1 k1=1
1=3k1+b1 b1=-2
∴y=x-2
练习5.1
答 案
如果一次函数y=kx+4与两坐标轴围成的三角形面积为4,则k= .
±2
解析
令y=0,x=
∴
k=±2.
方法展示
【示例】点P为x轴上一点,求CP+DP
最小时P的坐标.
解:点D作x轴对称点E,连接CE,
交x轴于点P,此时CP+DP最小. “将军饮马”问题
将C(-4,3),E(0,-3)代入y=kx+b;
解得 . 待定系数求CE解析式
点P在x轴上,令: -3=0得x= ;
∴P( , ) 求P坐标
一次函数中的“将军饮马”
答 案
-2
-2 0
数形结合,作出相应的辅助线,结合平面直角坐标系表示出相应的点坐标与数量关系
总结
一次函数中的“将军饮马”
例6
答 案
直线y= 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,请你在所给的坐标系中准确地画出点P的位置,并求出PC+PD值最小时点P的坐标.
P( ,0)
例6
解析
令y= 中,x=0,则y=4,
∴B( 0,4),
令y=0,则x=-6,
∴A(-6,0)
∵C、D分别为线段AB、OB的中点,
∴C(-3,2),D(0,2),
作D关于x轴对称点D',
∴D’(0,-2),
设直线CD‘解析式y=kx+b,
∴ 2=-3k+b k=
-2=b b=-2
∴y= x-2,
令y=0,则x=
∴P( ,0)
练习6.1
答 案
已知点A(0,2)、B(4,1),点P是x轴上的一点,则PA+PB的最小值是 .
5
作点A关于x轴的对称点A',连接A’B交x轴于点P,则P即为所求点.
∵点A(0,2)
∴点A关于x轴的对称点A‘的坐标为(0,-2),
∵A’(0,-2),B(4,1),
∴A‘B=
即PA+PB的最小值为5.
故答案为5.
解析
知识解读
一次函数与特殊三角形综合
引入
已知边AB,如何在坐标轴上找一点C,使得△ABC为等腰三角形?
两圆一线:
①若∠A为顶角.则点C在以 为圆心,以线段 为半径的小圆上;
②若∠B为顶角.则点C在以 为圆心,以线段 为半径的小圆上;
③若∠C为顶角.则点C在线段 的垂直平分线上;
一次函数与特殊三角形综合
答 案
A
讲解
AB
B
AB
AB
如图,在平面直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标
例7
解:(1)将点A(2,0)代入直线y=kx+3,
得0=2k+3,解得k= ,∴y= x+3.
当x=0时,y=3.∴B(0,3),OB=3.
当y=0时, x+3=0,∴x=2,
∴A(2,0),OA=2,
∴S△AOB= OA.OB= ×2×3=3.
(2)如图,符合条件的点C的坐标是
(-2,0)或( +2,0)或(2- ,0);
例7
答 案
练习7.1
答 案
已知一次函数y= x+1与x轴、y轴分别交于A、B两点,点P是坐标轴上的点,是否存在点P使得△ABP是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
存在,(-2- ,0)、(0,-1)、(2- ,0)、(0,3)、( ,0)、(- ,0).
Thank you
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
