2020湘教版八下数学第3章图形与坐标3.2简单图形的坐标表示习题课件(36张PPT)
文档属性
| 名称 | 2020湘教版八下数学第3章图形与坐标3.2简单图形的坐标表示习题课件(36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览










文档简介
课件36张PPT。3.2 简单图形的坐标表示1.会建立适当的坐标系确定点的坐标.(重点)
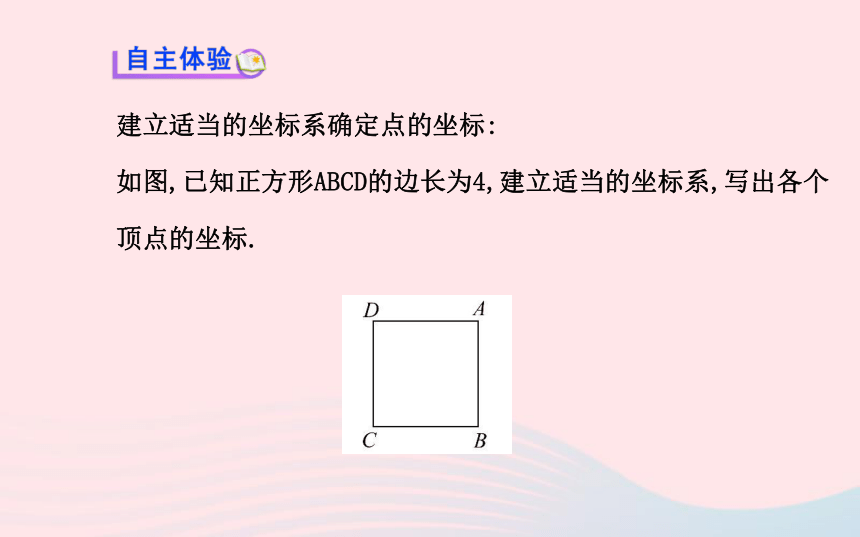
2.会在给定的坐标系下描出相应点的位置,并按要求连接成图.建立适当的坐标系确定点的坐标:
如图,已知正方形ABCD的边长为4,建立适当的坐标系,写出各个顶点的坐标.【思考】(1)如果以点C为坐标原点,分别以CB,CD所在的直线
为x轴、y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(4,4),B(4,0),C(0,0),D(0,4).
(2)如果以点A为坐标原点,分别以DA,AB所在的直线为x轴、
y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(0,0),B(0,-4),C(-4,-4),
D(-4,0).(3)如果以正方形的中心为坐标原点,分别以平行于DA,AB的直
线为x轴、y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(2,2),B(2,-2),C(-2,-2),
D(-2,2).【总结】(1)对于同一个图形,在不同的坐标系下各点的坐标是
_______.
(2)在不同的坐标系中,各点之间的相对位置与图形的特点是
_____的.不同的不变 (打“√”或“×”)
(1)在不同的坐标系下,图形同一个点的坐标不变化.( )
(2)同一个图形只能建立一个坐标系.( )
(3)建立坐标系一定要选水平和铅直方向为x轴和y轴.( )
(4)建立坐标系时,一定要以图形的一边为一条坐标轴.( )××××知识点 1 建立适当的直角坐标系确定点的坐标?
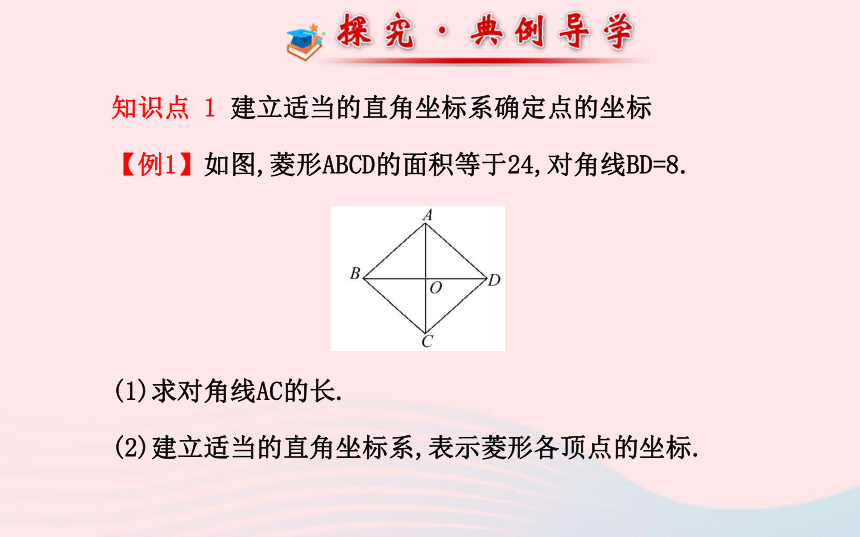
【例1】如图,菱形ABCD的面积等于24,对角线BD=8.
(1)求对角线AC的长.
(2)建立适当的直角坐标系,表示菱形各顶点的坐标.【思路点拨】(1)根据菱形的性质,S= BD·AC,即可求AC.
(2)根据菱形的性质,以菱形的对角线BD所在的直线为x轴,AC所
在直线为y轴建立直角坐标系,即可确定菱形四个顶点的坐标.【自主解答】(1)∵菱形的面积= BD·AC,
∴24= ×8×AC,∴AC=6.
(2)如图,以菱形的对角线BD所在直线为x轴,
AC所在直线为y轴建立直角坐标系.
由菱形的对角线互相垂直平分可知,OB=OD=4,OA=OC=3,
所以菱形四个顶点的坐标分别为A(0,3),B(-4,0),C(0,-3),
D(4,0).【总结提升】建立坐标系的常见方法
1.以某些特殊的线段所在的直线为x轴或y轴(如高线、中线等).
2.把对称图形的对称轴作为x轴或y轴.
3.以某个已知点为原点建立坐标系.知识点 2 根据点的坐标画图?
【例2】在直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0),(4,0),(2,2),(2,0).
(2)(0,2),(0,4),(-2,2),(0,2).
(3)(-4,0),(-2,-2),(-2,0),(-4,0).
(4)(0,-2),(2,-2),(0,-4),(0,-2).
观察所得的图形,你觉得它像什么?【思路点拨】建立适当的坐标系→描出各组点并依次连接各组中的每个点→判断图形的形状.
【自主解答】(1)(2)(3)(4)如图所示:
观察图形,它像一个风车.(答案不唯一)【总结提升】在平面直角坐标系中画图“三步法”
1.建系:根据题中点的坐标的特点建立适当的坐标系.
2.描点:根据各个点的坐标在坐标系中描出各点.
3.连线:依次连接坐标系中描出的点.
注:为防止画图时漏连、错连,在描点时要一边找点一边连线.题组一:建立适当的直角坐标系确定点的坐标
1.如图是在方格纸上画出的小旗图案,若用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为 ( )
A.(0,3) B.(2,3)
C.(3,2) D.(3,0)【解析】选C.用(0,0)表示A点,(0,4)表示B点,则以点A为坐标原点,AB所在直线为y轴,向上为正方向,x轴是过点A的水平直线,向右为正方向.所以点C的坐标为(3,2).2.课间操时,小华、小翠、小刚的位置如图,
小华对小翠说,如果你的位置用(0,0)表示,
小刚的位置用(2,3)表示,那么我的位置可
以表示成 ( )
A.(2,-1)
B.(-1,2)
C.(-2,-1)
D.(-1,-2)【解析】选C.小翠的位置用A(0,0)表示,小刚的位置用(2,3)表示,可知x轴是过点A的水平直线,y轴是过点A的铅直直线,所以小华的位置可以表示成(-2,-1).3.如图,每个小方格的边长为1,如果E点
的坐标是(-2,3),那么原点最可能在的
位置是 ( )
A.A点
B.B点
C.C点
D.D点【解析】选D.因为E点的坐标是(-2,3),则原点在E点右边2个单位长度,下方3个单位长度处,即D点的位置.4.有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为 .【解析】从图中可以看出有序数对(5,3),(6,3),(7,3),(4,1),
(4,4)分别对应的字母为S,T,U,D,Y.所以这个英文单词写出来
为“STUDY”,翻译成中文为“学习”.
答案:STUDY(学习)5.如图,在直角梯形ABCD中,上底BC=3cm,下底
AD=5cm,底角∠D=45°,建立适当的平面直角坐
标系,并写出四个顶点的坐标.
【解析】建立平面直角坐标系如图,A(0,0),作CE⊥AD,垂足为E.因为∠EDC=45°,∠CED=90°,
所以∠ECD=45°,所以CE=ED,
所以CE=ED=5-3=2.
所以B(0,2),C(3,2),D(5,0).题组二:根据点的坐标画图
1.在坐标系内,由A(1,2),B(-3,2),C(1,-1)三点组成的三角形是 ( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.等边三角形
【解析】选A.A,B两点的纵坐标相同,所以AB⊥y轴,A,C两点的横坐标相同,所以AC∥y轴,所以AB⊥AC,所以△ABC为直角三角形.2.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4).
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是 ( )
A.两个三角形 B.房子 C.雨伞 D.电灯【解析】选C.在平面直角坐标系中,根据第(1)组数据确定点,依次连接可以得到一个类似竖弯钩的图象;根据第(2)组的数据确定各点,依次连接可以得到一个三角形的图象;且这两个图象在(3,4)点相交,这两个图象连起来看是一个雨伞的图案(如图所示).【变式训练】在直角坐标系内顺次连接下列各点,不能得到正方形的是 ( )
A.(-2,2),(2,2),(2,-2),(-2,-2),(-2,2)
B.(0,0),(2,0),(2,2),(0,2),(0,0)
C.(0,0),(0,2),(2,-2),(-2,0),(0,0)
D.(-1,-1),(-1,1),(1,1),(1,-1),(-1,-1)【解析】选C.通过画图可知C得到的图形如下:3.在平面直角坐标系中,点A(-3,0),B(5,0),C(0,4)所组成的三
角形ABC的面积是 ( )
A.32 B.4 C.16 D.8
【解析】选C.∵A(-3,0),B(5,0),C(0,4),∴AB=8.∴三角形ABC
的面积是 ×8×4=4×4=16.4.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是( ),破译“正做数学”的真实意思是“ ”.【解析】由图结合题意可以看出,将每个字先向右移动一个格,再向上移动两个格,看到的字就是它的真实意思,所以(x,y)的对应点是(x+1,y+2);“正做数学”的真实意思是“祝你成功”.
答案:x+1,y+2 祝你成功5.已知平面直角坐标系中,有四个点A(-3,0),B(0,-4),C(3,0),
D(0,4),
(1)在给出的平面直角坐标系中描出各点,并顺次连接,试判断
所得四边形的形状,并说明理由.
(2)若以A,B,C,E四点为顶点的四边形是平行四边形,请你直接
写出点E的坐标.【解析】(1)根据题意作图得:
四边形ABCD为菱形,∵△OAB≌△OCB≌△OCD≌△OAD,
∴AB=BC=CD=DA,
∴四边形ABCD为菱形.
(2)若ABCE为平行四边形,即AE?? BC,CE?? AB,
可以看出点E即(1)中点D,
∴点E的坐标为(0,4).
若四边形AEBC为平行四边形,则点E的坐标为(-6,-4).
若四边形ABEC为平行四边形,则点E的坐标为(6,-4).
综上可知,点E的坐标为(0,4)或(-6,-4)或(6,-4).【想一想错在哪?】如图是象棋盘的一部分.若“帅”位于点(1,-2),“相”位于点(3,-2),则“炮”位于点 ( )
A.(1,3) B.(-1,2) C.(-2,1) D.(-2,2)提示:没有由“帅”与“相”的位置确定原点位置,误认为左下角的点为坐标原点.
2.会在给定的坐标系下描出相应点的位置,并按要求连接成图.建立适当的坐标系确定点的坐标:
如图,已知正方形ABCD的边长为4,建立适当的坐标系,写出各个顶点的坐标.【思考】(1)如果以点C为坐标原点,分别以CB,CD所在的直线
为x轴、y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(4,4),B(4,0),C(0,0),D(0,4).
(2)如果以点A为坐标原点,分别以DA,AB所在的直线为x轴、
y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(0,0),B(0,-4),C(-4,-4),
D(-4,0).(3)如果以正方形的中心为坐标原点,分别以平行于DA,AB的直
线为x轴、y轴建立直角坐标系,那么各个顶点的坐标是什么?
提示:A,B,C,D的坐标分别为A(2,2),B(2,-2),C(-2,-2),
D(-2,2).【总结】(1)对于同一个图形,在不同的坐标系下各点的坐标是
_______.
(2)在不同的坐标系中,各点之间的相对位置与图形的特点是
_____的.不同的不变 (打“√”或“×”)
(1)在不同的坐标系下,图形同一个点的坐标不变化.( )
(2)同一个图形只能建立一个坐标系.( )
(3)建立坐标系一定要选水平和铅直方向为x轴和y轴.( )
(4)建立坐标系时,一定要以图形的一边为一条坐标轴.( )××××知识点 1 建立适当的直角坐标系确定点的坐标?
【例1】如图,菱形ABCD的面积等于24,对角线BD=8.
(1)求对角线AC的长.
(2)建立适当的直角坐标系,表示菱形各顶点的坐标.【思路点拨】(1)根据菱形的性质,S= BD·AC,即可求AC.
(2)根据菱形的性质,以菱形的对角线BD所在的直线为x轴,AC所
在直线为y轴建立直角坐标系,即可确定菱形四个顶点的坐标.【自主解答】(1)∵菱形的面积= BD·AC,
∴24= ×8×AC,∴AC=6.
(2)如图,以菱形的对角线BD所在直线为x轴,
AC所在直线为y轴建立直角坐标系.
由菱形的对角线互相垂直平分可知,OB=OD=4,OA=OC=3,
所以菱形四个顶点的坐标分别为A(0,3),B(-4,0),C(0,-3),
D(4,0).【总结提升】建立坐标系的常见方法
1.以某些特殊的线段所在的直线为x轴或y轴(如高线、中线等).
2.把对称图形的对称轴作为x轴或y轴.
3.以某个已知点为原点建立坐标系.知识点 2 根据点的坐标画图?
【例2】在直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0),(4,0),(2,2),(2,0).
(2)(0,2),(0,4),(-2,2),(0,2).
(3)(-4,0),(-2,-2),(-2,0),(-4,0).
(4)(0,-2),(2,-2),(0,-4),(0,-2).
观察所得的图形,你觉得它像什么?【思路点拨】建立适当的坐标系→描出各组点并依次连接各组中的每个点→判断图形的形状.
【自主解答】(1)(2)(3)(4)如图所示:
观察图形,它像一个风车.(答案不唯一)【总结提升】在平面直角坐标系中画图“三步法”
1.建系:根据题中点的坐标的特点建立适当的坐标系.
2.描点:根据各个点的坐标在坐标系中描出各点.
3.连线:依次连接坐标系中描出的点.
注:为防止画图时漏连、错连,在描点时要一边找点一边连线.题组一:建立适当的直角坐标系确定点的坐标
1.如图是在方格纸上画出的小旗图案,若用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为 ( )
A.(0,3) B.(2,3)
C.(3,2) D.(3,0)【解析】选C.用(0,0)表示A点,(0,4)表示B点,则以点A为坐标原点,AB所在直线为y轴,向上为正方向,x轴是过点A的水平直线,向右为正方向.所以点C的坐标为(3,2).2.课间操时,小华、小翠、小刚的位置如图,
小华对小翠说,如果你的位置用(0,0)表示,
小刚的位置用(2,3)表示,那么我的位置可
以表示成 ( )
A.(2,-1)
B.(-1,2)
C.(-2,-1)
D.(-1,-2)【解析】选C.小翠的位置用A(0,0)表示,小刚的位置用(2,3)表示,可知x轴是过点A的水平直线,y轴是过点A的铅直直线,所以小华的位置可以表示成(-2,-1).3.如图,每个小方格的边长为1,如果E点
的坐标是(-2,3),那么原点最可能在的
位置是 ( )
A.A点
B.B点
C.C点
D.D点【解析】选D.因为E点的坐标是(-2,3),则原点在E点右边2个单位长度,下方3个单位长度处,即D点的位置.4.有一个英文单词的字母顺序对应如图中的有序数对分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文为 .【解析】从图中可以看出有序数对(5,3),(6,3),(7,3),(4,1),
(4,4)分别对应的字母为S,T,U,D,Y.所以这个英文单词写出来
为“STUDY”,翻译成中文为“学习”.
答案:STUDY(学习)5.如图,在直角梯形ABCD中,上底BC=3cm,下底
AD=5cm,底角∠D=45°,建立适当的平面直角坐
标系,并写出四个顶点的坐标.
【解析】建立平面直角坐标系如图,A(0,0),作CE⊥AD,垂足为E.因为∠EDC=45°,∠CED=90°,
所以∠ECD=45°,所以CE=ED,
所以CE=ED=5-3=2.
所以B(0,2),C(3,2),D(5,0).题组二:根据点的坐标画图
1.在坐标系内,由A(1,2),B(-3,2),C(1,-1)三点组成的三角形是 ( )
A.直角三角形 B.钝角三角形
C.锐角三角形 D.等边三角形
【解析】选A.A,B两点的纵坐标相同,所以AB⊥y轴,A,C两点的横坐标相同,所以AC∥y轴,所以AB⊥AC,所以△ABC为直角三角形.2.在平面直角坐标系中,依次描出下列各点,并将各组内的点依次连接起来:
(1)(2,1),(2,0),(3,0),(3,4).
(2)(3,6),(0,4),(6,4),(3,6).
你发现所得的图形是 ( )
A.两个三角形 B.房子 C.雨伞 D.电灯【解析】选C.在平面直角坐标系中,根据第(1)组数据确定点,依次连接可以得到一个类似竖弯钩的图象;根据第(2)组的数据确定各点,依次连接可以得到一个三角形的图象;且这两个图象在(3,4)点相交,这两个图象连起来看是一个雨伞的图案(如图所示).【变式训练】在直角坐标系内顺次连接下列各点,不能得到正方形的是 ( )
A.(-2,2),(2,2),(2,-2),(-2,-2),(-2,2)
B.(0,0),(2,0),(2,2),(0,2),(0,0)
C.(0,0),(0,2),(2,-2),(-2,0),(0,0)
D.(-1,-1),(-1,1),(1,1),(1,-1),(-1,-1)【解析】选C.通过画图可知C得到的图形如下:3.在平面直角坐标系中,点A(-3,0),B(5,0),C(0,4)所组成的三
角形ABC的面积是 ( )
A.32 B.4 C.16 D.8
【解析】选C.∵A(-3,0),B(5,0),C(0,4),∴AB=8.∴三角形ABC
的面积是 ×8×4=4×4=16.4.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是( ),破译“正做数学”的真实意思是“ ”.【解析】由图结合题意可以看出,将每个字先向右移动一个格,再向上移动两个格,看到的字就是它的真实意思,所以(x,y)的对应点是(x+1,y+2);“正做数学”的真实意思是“祝你成功”.
答案:x+1,y+2 祝你成功5.已知平面直角坐标系中,有四个点A(-3,0),B(0,-4),C(3,0),
D(0,4),
(1)在给出的平面直角坐标系中描出各点,并顺次连接,试判断
所得四边形的形状,并说明理由.
(2)若以A,B,C,E四点为顶点的四边形是平行四边形,请你直接
写出点E的坐标.【解析】(1)根据题意作图得:
四边形ABCD为菱形,∵△OAB≌△OCB≌△OCD≌△OAD,
∴AB=BC=CD=DA,
∴四边形ABCD为菱形.
(2)若ABCE为平行四边形,即AE?? BC,CE?? AB,
可以看出点E即(1)中点D,
∴点E的坐标为(0,4).
若四边形AEBC为平行四边形,则点E的坐标为(-6,-4).
若四边形ABEC为平行四边形,则点E的坐标为(6,-4).
综上可知,点E的坐标为(0,4)或(-6,-4)或(6,-4).【想一想错在哪?】如图是象棋盘的一部分.若“帅”位于点(1,-2),“相”位于点(3,-2),则“炮”位于点 ( )
A.(1,3) B.(-1,2) C.(-2,1) D.(-2,2)提示:没有由“帅”与“相”的位置确定原点位置,误认为左下角的点为坐标原点.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
