2020湘教版八下数学第3章图形与坐标阶段专题复习习题课件(33张PPT)
文档属性
| 名称 | 2020湘教版八下数学第3章图形与坐标阶段专题复习习题课件(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 671.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 21:52:07 | ||
图片预览









文档简介
课件33张PPT。阶段专题复习
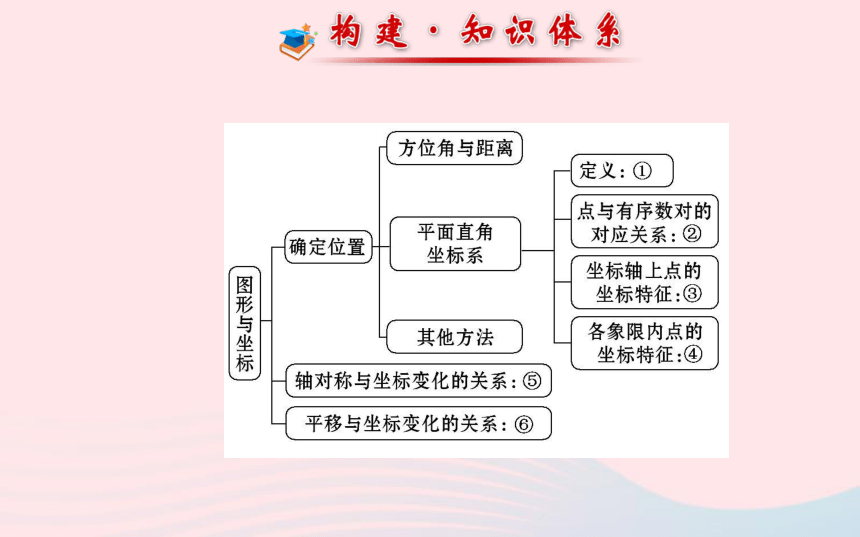
第 3 章请写出框图中数字处的内容:
①____________________________________________________
______________________________________________________
_____________________________________________________
_____;
②_______________________________;
③________________________________________;平面内画两条互相垂直的数轴,其中一条叫横轴(x轴),另一条叫纵轴(y轴),它们的交点是两个数轴的原点,横轴向右是正方向,纵轴向上为正方向,这样的两条数轴组成了平面直角坐标系平面上的点与有序实数对一一对应横轴上的点纵坐标为0,纵轴上的点横坐标为0④___________________________________________________
______________________________;
⑤___________________________________________________
___________________________________________;
⑥____________________________________________________
_____________________________________________________
___________________________________________________.第一象限的点为(+,+),第二象限的点为(-,+),第三象限的点为(-,-),第四象限的点为(+,-)一般地,在平面直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点的坐标为(-a,b)一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位,其像的坐标为(a,b+k)(或(a,b-k))考点 1 点的坐标特征?
【知识点睛】
各象限内及坐标轴上的点P(a,b)的特征如下:
(1)a>0,b>0 点在第一象限.
(2)a<0,b>0 点在第二象限.
(3)a<0,b<0 点在第三象限.
(4)a>0,b<0 点在第四象限.(5)a=0 点在y轴上.
(6)b=0 点在x轴上.
(7)a=0,b=0 点在原点上.【例1】在平面直角坐标系中,点(2,-4)在
第 象限.
【思路点拨】根据各象限内点的坐标特征解答.
【自主解答】∵2>0,-4<0,根据象限内点的坐标特征,可知第
四象限点的特征是(+,-),∴点(2,-4)在第四象限.
答案:四【中考集训】
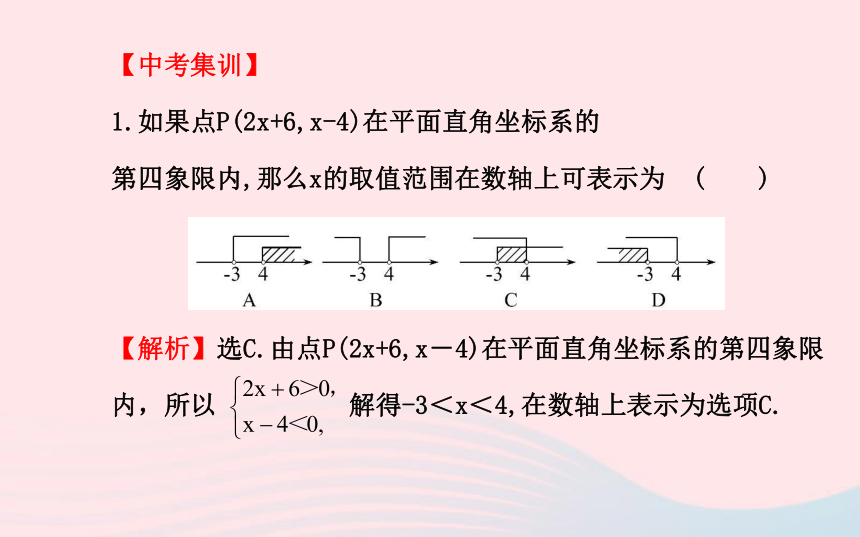
1.如果点P(2x+6,x-4)在平面直角坐标系的
第四象限内,那么x的取值范围在数轴上可表示为 ( )
【解析】选C.由点P(2x+6,x-4)在平面直角坐标系的第四象限
内,所以 解得-3<x<4,在数轴上表示为选项C.2.在平面直角坐标系中,线段OP的两个端点坐标分别为O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP'位置,则点P'的坐标为 ( )
A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)
【解析】选C.如图,过点P作PA⊥x轴于点A,设点A旋转后的对应点为A',则P'A'=PA=3,OA'=OA=4,∴点P'的坐标为(-3,4).3.写出一个第二象限内的点的坐标 .
【解析】第二象限的点的坐标特征是(-,+),如(-1,1)为第二象限的一个点.
答案:(-1,1)(答案不唯一)4.第二象限内的点P(x,y)满足|x|=5,
y2=4,则点P的坐标是 .
【解析】∵|x|=5,y2=4,∴x=±5,y=±2,
∵点P(x,y)在第二象限,∴x<0,y>0,
∴x=-5,y=2,∴点P的坐标为(-5,2).
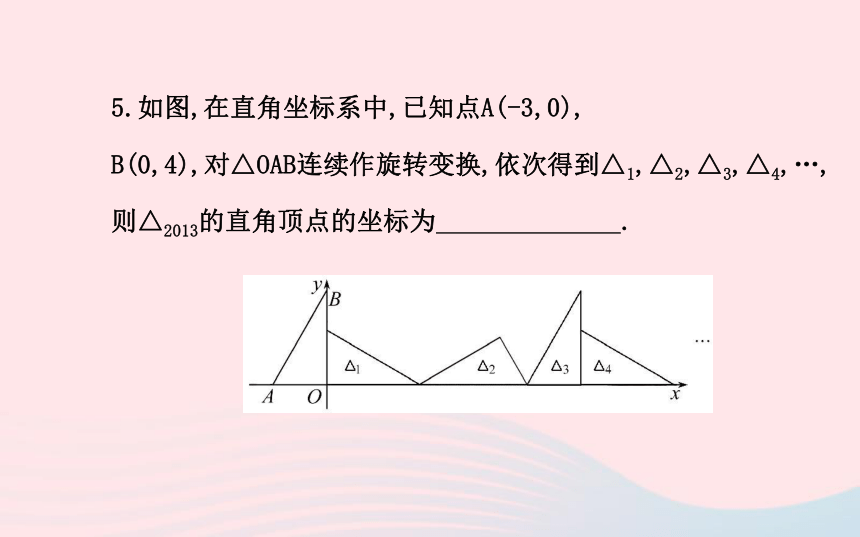
答案:(-5,2)5.如图,在直角坐标系中,已知点A(-3,0),
B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,
则△2013的直角顶点的坐标为 .【解析】∵点A(-3,0),B(0,4),∴OB=4,OA=3,∴AB=5,∵对△OAB连续作如图所示的旋转变换,∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,而2013=671×3,∴第2013个三角形和△3状态一样,∴△2013的直角顶点的横坐标为671×12=8052,纵坐标为0.
答案:(8052,0)考点 2 轴对称与坐标变化?
【知识点睛】
关于坐标轴对称的点的特征:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.【例2】点(3,2)关于x轴的对称点为( )
A.(3,-2) B.(-3,2)
C.(-3,-2) D.(2,-3)
【思路点拨】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可直接写出答案.
【自主解答】选A.点(3,2)关于x轴的对称点为(3,-2).【中考集训】
1.如图,在直角坐标系中,
点A,B的坐标分别为(1,4)和(3,0),点C是y
轴上的一个动点,且A,B,C三点不在同一条
直线上,当△ABC的周长最小时,点C的坐标
是 ( )
A.(0,0) B.(0,1)
C.(0,2) D.(0,3)【解析】选D.作B点关于y轴对称点B'点,连接AB',
交y轴于点C',作AE⊥x轴,垂足为E,此时
△ABC的周长最小,
∵点A,B的坐标分别为(1,4)和(3,0),
∴B'点坐标为(-3,0),AE=4,则B'E=4,即B'E=AE,
∵C'O∥AE,∴B'O=C'O=3,∴点C'的坐标是(0,3),此时△ABC的周长最小.2.平面直角坐标系中,点A(2,0)关于y轴对称的点A'的坐标为 .
【解析】∵关于y轴对称的两个点的纵坐标不变,横坐标互为相反数,
∴点A(2,0)关于y轴对称的点A'的坐标为(-2,0).
答案:(-2,0)3.点P(2,-1)关于x轴对称的点P'的坐标是 .
【解析】∵关于x轴对称的两个点的横坐标相同,纵坐标互为相反数,
∴点(2,-1)关于x轴的对称点坐标是(2,1).
答案:(2,1)【归纳整合】掌握关于x轴的对称点的坐标,y轴的对称点的坐标特征,有利于求点的坐标和确定点的位置,这些知识在与坐标对称有关的题目中经常用到.考点 3 图形的平移与坐标变化?
【知识点睛】
平移前后点的坐标特征:
(1)一个点向左(右)平移k个单位后,其像点的横坐标减小(增加)k,纵坐标不变.
(2)一个点向上(下)平移k个单位后,其像点的纵坐标增加(减小)k,横坐标不变.【例3】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)画出平移后的△A'B'C',并直接写出点A',B',C'的坐标.
(2)求出在整个平移过程中,线段AB扫过的面积.【思路点拨】(1)根据网格结构找出点A',B',C'的位置,然后顺次连接即可,再根据平面直角坐标系写出坐标即可.
(2)线段AB扫过的面积为平行四边形AA'B'B的面积,然后列式进行计算即可得解.【自主解答】(1)平移后的△A'B'C'如图所示:
点A',B',C'的坐标分别为(-1,5),(-4,0),(-1,0).(2)由平移的性质可知,四边形AA'B'B是平行四边形,
所以线段AB扫过的面积
=S四边形AA'B'B=B'B·AC
=5×5=25.【中考集训】
1.在如图所示的单位
正方形网格中,△ABC经过平移后得到
△A1B1C1,已知在AC上一点P(2.4,2)平
移后的对应点为P1,点P1绕点O逆时针
旋转180°,得到对应点P2,则P2点的坐标为 ( )
A.(1.4,-1) B.(1.5,2)
C.(1.6,1) D.(2.4,1) 【解析】选C.∵点A的坐标为(2,4),点A1的坐标为(-2,1),
∴点P(2.4,2)平移后的对应点P1为(-1.6,-1),
∵点P1绕点O逆时针旋转180°,得到对应点P2,
∴P2点的坐标为(1.6,1).2.在平面直角坐标系中,将线段OA向左平移2
个单位,平移后,点O,A的像点分别为点O1,A1.若点O(0,0),
A(1,4),则点O1,A1的坐标分别是 ( )
A.(0,0),(1,4) B.(0,0),(3,4)
C.(-2,0),(1,4) D.(-2,0),(-1,4)
【解析】选D.∵线段OA向左平移2个单位,
∴点O1的坐标为(0-2,0),即(-2,0),
点A1的坐标为(1-2,4),即(-1,4).3.如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,右眼B的坐标是 .【解析】因为点A,B关于点C所在的纵向的网格线对称,根据对称性可知右眼的坐标为(0,3),再将右眼向右平移3个单位后的点B的坐标为(3,3).
答案:(3,3)4.如图,在平面直角坐标系
xOy中,点A的坐标为(-2,0),等边三角形AOC经
过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是_______个
单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;
△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是_______
度.
(2)连接AD,交OC于点E,求∠AEO的度数.【解析】(1)∵点A的坐标为(-2,0),
∴△AOC沿x轴向右平移2个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
答案:2 y轴 120(2)如图所示:
由旋转得OA=OD,∠AOD=120°,
因为△AOC是等边三角形,
所以∠AOC=60°,
所以∠COD=∠AOD-∠AOC=60°,
所以∠COD=∠AOC,
又因为OA=OD,所以OC⊥AD,所以∠AEO=90°.
第 3 章请写出框图中数字处的内容:
①____________________________________________________
______________________________________________________
_____________________________________________________
_____;
②_______________________________;
③________________________________________;平面内画两条互相垂直的数轴,其中一条叫横轴(x轴),另一条叫纵轴(y轴),它们的交点是两个数轴的原点,横轴向右是正方向,纵轴向上为正方向,这样的两条数轴组成了平面直角坐标系平面上的点与有序实数对一一对应横轴上的点纵坐标为0,纵轴上的点横坐标为0④___________________________________________________
______________________________;
⑤___________________________________________________
___________________________________________;
⑥____________________________________________________
_____________________________________________________
___________________________________________________.第一象限的点为(+,+),第二象限的点为(-,+),第三象限的点为(-,-),第四象限的点为(+,-)一般地,在平面直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点的坐标为(-a,b)一般地,在平面直角坐标系中,将点(a,b)向右(或向左)平移k个单位,其像的坐标为(a+k,b)(或(a-k,b));将点(a,b)向上(或向下)平移k个单位,其像的坐标为(a,b+k)(或(a,b-k))考点 1 点的坐标特征?
【知识点睛】
各象限内及坐标轴上的点P(a,b)的特征如下:
(1)a>0,b>0 点在第一象限.
(2)a<0,b>0 点在第二象限.
(3)a<0,b<0 点在第三象限.
(4)a>0,b<0 点在第四象限.(5)a=0 点在y轴上.
(6)b=0 点在x轴上.
(7)a=0,b=0 点在原点上.【例1】在平面直角坐标系中,点(2,-4)在
第 象限.
【思路点拨】根据各象限内点的坐标特征解答.
【自主解答】∵2>0,-4<0,根据象限内点的坐标特征,可知第
四象限点的特征是(+,-),∴点(2,-4)在第四象限.
答案:四【中考集训】
1.如果点P(2x+6,x-4)在平面直角坐标系的
第四象限内,那么x的取值范围在数轴上可表示为 ( )
【解析】选C.由点P(2x+6,x-4)在平面直角坐标系的第四象限
内,所以 解得-3<x<4,在数轴上表示为选项C.2.在平面直角坐标系中,线段OP的两个端点坐标分别为O(0,0),P(4,3),将线段OP绕点O逆时针旋转90°到OP'位置,则点P'的坐标为 ( )
A.(3,4) B.(-4,3) C.(-3,4) D.(4,-3)
【解析】选C.如图,过点P作PA⊥x轴于点A,设点A旋转后的对应点为A',则P'A'=PA=3,OA'=OA=4,∴点P'的坐标为(-3,4).3.写出一个第二象限内的点的坐标 .
【解析】第二象限的点的坐标特征是(-,+),如(-1,1)为第二象限的一个点.
答案:(-1,1)(答案不唯一)4.第二象限内的点P(x,y)满足|x|=5,
y2=4,则点P的坐标是 .
【解析】∵|x|=5,y2=4,∴x=±5,y=±2,
∵点P(x,y)在第二象限,∴x<0,y>0,
∴x=-5,y=2,∴点P的坐标为(-5,2).
答案:(-5,2)5.如图,在直角坐标系中,已知点A(-3,0),
B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,
则△2013的直角顶点的坐标为 .【解析】∵点A(-3,0),B(0,4),∴OB=4,OA=3,∴AB=5,∵对△OAB连续作如图所示的旋转变换,∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,而2013=671×3,∴第2013个三角形和△3状态一样,∴△2013的直角顶点的横坐标为671×12=8052,纵坐标为0.
答案:(8052,0)考点 2 轴对称与坐标变化?
【知识点睛】
关于坐标轴对称的点的特征:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.【例2】点(3,2)关于x轴的对称点为( )
A.(3,-2) B.(-3,2)
C.(-3,-2) D.(2,-3)
【思路点拨】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可直接写出答案.
【自主解答】选A.点(3,2)关于x轴的对称点为(3,-2).【中考集训】
1.如图,在直角坐标系中,
点A,B的坐标分别为(1,4)和(3,0),点C是y
轴上的一个动点,且A,B,C三点不在同一条
直线上,当△ABC的周长最小时,点C的坐标
是 ( )
A.(0,0) B.(0,1)
C.(0,2) D.(0,3)【解析】选D.作B点关于y轴对称点B'点,连接AB',
交y轴于点C',作AE⊥x轴,垂足为E,此时
△ABC的周长最小,
∵点A,B的坐标分别为(1,4)和(3,0),
∴B'点坐标为(-3,0),AE=4,则B'E=4,即B'E=AE,
∵C'O∥AE,∴B'O=C'O=3,∴点C'的坐标是(0,3),此时△ABC的周长最小.2.平面直角坐标系中,点A(2,0)关于y轴对称的点A'的坐标为 .
【解析】∵关于y轴对称的两个点的纵坐标不变,横坐标互为相反数,
∴点A(2,0)关于y轴对称的点A'的坐标为(-2,0).
答案:(-2,0)3.点P(2,-1)关于x轴对称的点P'的坐标是 .
【解析】∵关于x轴对称的两个点的横坐标相同,纵坐标互为相反数,
∴点(2,-1)关于x轴的对称点坐标是(2,1).
答案:(2,1)【归纳整合】掌握关于x轴的对称点的坐标,y轴的对称点的坐标特征,有利于求点的坐标和确定点的位置,这些知识在与坐标对称有关的题目中经常用到.考点 3 图形的平移与坐标变化?
【知识点睛】
平移前后点的坐标特征:
(1)一个点向左(右)平移k个单位后,其像点的横坐标减小(增加)k,纵坐标不变.
(2)一个点向上(下)平移k个单位后,其像点的纵坐标增加(减小)k,横坐标不变.【例3】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)画出平移后的△A'B'C',并直接写出点A',B',C'的坐标.
(2)求出在整个平移过程中,线段AB扫过的面积.【思路点拨】(1)根据网格结构找出点A',B',C'的位置,然后顺次连接即可,再根据平面直角坐标系写出坐标即可.
(2)线段AB扫过的面积为平行四边形AA'B'B的面积,然后列式进行计算即可得解.【自主解答】(1)平移后的△A'B'C'如图所示:
点A',B',C'的坐标分别为(-1,5),(-4,0),(-1,0).(2)由平移的性质可知,四边形AA'B'B是平行四边形,
所以线段AB扫过的面积
=S四边形AA'B'B=B'B·AC
=5×5=25.【中考集训】
1.在如图所示的单位
正方形网格中,△ABC经过平移后得到
△A1B1C1,已知在AC上一点P(2.4,2)平
移后的对应点为P1,点P1绕点O逆时针
旋转180°,得到对应点P2,则P2点的坐标为 ( )
A.(1.4,-1) B.(1.5,2)
C.(1.6,1) D.(2.4,1) 【解析】选C.∵点A的坐标为(2,4),点A1的坐标为(-2,1),
∴点P(2.4,2)平移后的对应点P1为(-1.6,-1),
∵点P1绕点O逆时针旋转180°,得到对应点P2,
∴P2点的坐标为(1.6,1).2.在平面直角坐标系中,将线段OA向左平移2
个单位,平移后,点O,A的像点分别为点O1,A1.若点O(0,0),
A(1,4),则点O1,A1的坐标分别是 ( )
A.(0,0),(1,4) B.(0,0),(3,4)
C.(-2,0),(1,4) D.(-2,0),(-1,4)
【解析】选D.∵线段OA向左平移2个单位,
∴点O1的坐标为(0-2,0),即(-2,0),
点A1的坐标为(1-2,4),即(-1,4).3.如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,右眼B的坐标是 .【解析】因为点A,B关于点C所在的纵向的网格线对称,根据对称性可知右眼的坐标为(0,3),再将右眼向右平移3个单位后的点B的坐标为(3,3).
答案:(3,3)4.如图,在平面直角坐标系
xOy中,点A的坐标为(-2,0),等边三角形AOC经
过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是_______个
单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;
△AOC绕原点O顺时针旋转得到△DOB,则旋转角可以是_______
度.
(2)连接AD,交OC于点E,求∠AEO的度数.【解析】(1)∵点A的坐标为(-2,0),
∴△AOC沿x轴向右平移2个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
答案:2 y轴 120(2)如图所示:
由旋转得OA=OD,∠AOD=120°,
因为△AOC是等边三角形,
所以∠AOC=60°,
所以∠COD=∠AOD-∠AOC=60°,
所以∠COD=∠AOC,
又因为OA=OD,所以OC⊥AD,所以∠AEO=90°.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
