2020湘教版八下数学第3章图形与坐标3.3轴对称和平移的坐标表示第1课时教学课件(18张PPT)
文档属性
| 名称 | 2020湘教版八下数学第3章图形与坐标3.3轴对称和平移的坐标表示第1课时教学课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 00:00:00 | ||
图片预览





文档简介
课件18张PPT。3.3 轴对称和平移的坐标表示第1课时xy1.通过在实践活动中探究,发现在平面直角坐标系中,关于x轴和y轴对称的点的规律,从而发展学生数形结合的思想,激发求知欲和好奇心.
2.能够利用x轴和y轴对称的点的规律,作出关于x轴和 y轴对称的图形.
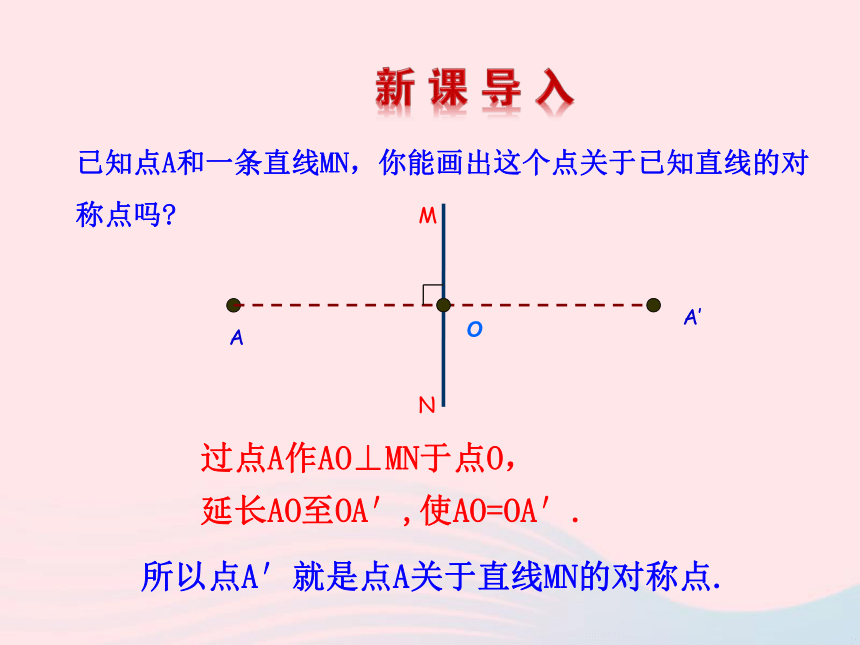
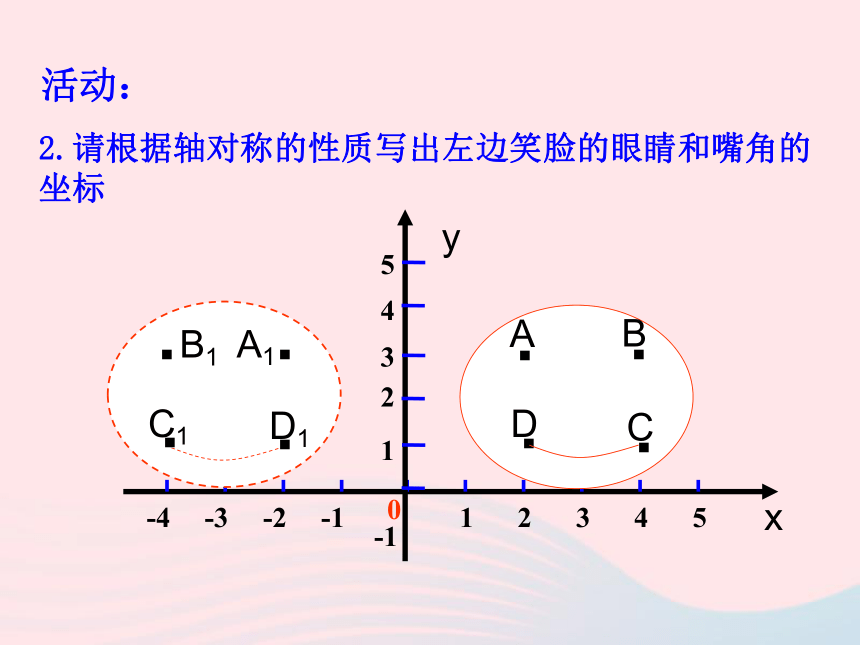
3.理解图形上的点的坐标的变化与图形的轴对称变换 之间的关系.已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?AA′MN所以点A′就是点A关于直线MN的对称点.O延长AO至OA′,使AO=OA′.过点A作AO⊥MN于点O,活动: 1.观察图中两个笑脸有什么关系?轴对称关系(关于y轴对称)活动:2.请根据轴对称的性质写出左边笑脸的眼睛和嘴角的坐标····ABCD··A1B1··x活动:A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________(-2,3)(-4,3)(-4,1)(-2,1)C1D1(4,3)(2,3)(4,1)(2,1)(一)引导学生从活动中归纳:关于x轴对称的点的坐标的特点是:横坐标相等,纵坐标互为相反数.练一练
1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,
b =_____.(- 5, -6 )-25(二)引导学生从活动中归纳:关于y轴对称的点的坐标的特点是:横坐标互为相反数,纵坐标相等.练一练
1.点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为
__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____,
b =_____.( 5 , 6 )2-5已知△ABC的三个顶点的坐标分别为A(-3,5),
B(- 4,1),C(-1,3),作出△ABC关于y轴对称的
图形.【解析】点A(-3,5),
B(-4,1),C(-1,3),关于y轴对称的点的坐标分别为A′(3,5), B′ (4,1),
C′ (1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的△A′B′C′.AB′
A′C′····【例题】xy归纳:对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.1.如图所示,请分别画出△ABC在直角坐标系中关于y轴,x轴对称的三角形······【跟踪训练】ABCDA′B′C′D′·······2.四边形ABCD的四个顶点的坐标分别是A(-5,1),
B(-2,1),C(-2,5),D(-5,4),作出与四边形ABCD关于y轴对称的图形.·0 1 2 3 4 5 6 7 8 9 1087654321
-1-2-3-4y3.图中小鱼各顶点的横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来.此时,所得图案与原图案相比有什么变化?关于x轴对称x1.完成下表(-1,-2)(1,2)(-4,-3)(4, 3)(6, -7)(-6,7)(-5, 1)(5,-1)(-9,0)(9,0)2.完成下表(-2,-3)(2,3)(-1,-2)(1, 2)(6, -5)(-6, 5)(-0.5, 1)(0.5,-1)(-4,0)(4,0)4.已知点P(6, b+2)与点P ′(a+b, -3a).
若点P与点P ′关于x轴对称,则a=_____ b=_______.
若点P与点P ′关于y轴对称,则a=_____ b=_______.242-83.已知点P(6, 2)与点P ′(b, -a).
若点P与点P′关于x轴对称,则a=_____ b=_______.
若点P与点P ′关于y轴对称,则a=_____ b=_______.26-2-65.已知线段AB的两个端点的坐标分别为A(-4,1),
B(-1,4),作出线段AB关于y轴对称的图形.··A(-4,1)B(-1,4)A'(4,1)B'(1,4)【解析】点A(-4,1),B(-1,4)关于y轴对称的点的坐标分别为A′(4,1),B′ (1,4).连接A′,B′,就得到线段AB关于y轴对称的线段A′B′.··1.学习了在平面直角坐标系中关于x轴和y轴对称的点的坐标的特点.关于x轴对称的点的横坐标相等,纵坐标互为相反数.关于y轴对称的点的横坐标互为相反数,纵坐标相等.2.学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形.先求出已知图形中的一些特殊点(如多边形的顶点)的对应
点的坐标,描出并连接这些点,就可以得到这个图形的轴对
称图形. 古之立大事者,不惟有超世之才,亦必有坚忍不拔之志.
—— 苏 轼
2.能够利用x轴和y轴对称的点的规律,作出关于x轴和 y轴对称的图形.
3.理解图形上的点的坐标的变化与图形的轴对称变换 之间的关系.已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗?AA′MN所以点A′就是点A关于直线MN的对称点.O延长AO至OA′,使AO=OA′.过点A作AO⊥MN于点O,活动: 1.观察图中两个笑脸有什么关系?轴对称关系(关于y轴对称)活动:2.请根据轴对称的性质写出左边笑脸的眼睛和嘴角的坐标····ABCD··A1B1··x活动:A1的坐标为_________ B1的坐标为________
C1的坐标为_________ D1的坐标为________(-2,3)(-4,3)(-4,1)(-2,1)C1D1(4,3)(2,3)(4,1)(2,1)(一)引导学生从活动中归纳:关于x轴对称的点的坐标的特点是:横坐标相等,纵坐标互为相反数.练一练
1.点P(-5, 6)与点Q关于x轴对称,则点Q的坐标为__________.
2.点M(a, -5)与点N(-2, b)关于x轴对称,则a=_____,
b =_____.(- 5, -6 )-25(二)引导学生从活动中归纳:关于y轴对称的点的坐标的特点是:横坐标互为相反数,纵坐标相等.练一练
1.点P(-5, 6)与点Q关于y轴对称,则点Q的坐标为
__________.
2.点M(a, -5)与点N(-2, b)关于y轴对称,则a=_____,
b =_____.( 5 , 6 )2-5已知△ABC的三个顶点的坐标分别为A(-3,5),
B(- 4,1),C(-1,3),作出△ABC关于y轴对称的
图形.【解析】点A(-3,5),
B(-4,1),C(-1,3),关于y轴对称的点的坐标分别为A′(3,5), B′ (4,1),
C′ (1,3).依次连接A′B′,B′C′,C′A′,就得到△ABC关于y轴对称的△A′B′C′.AB′
A′C′····【例题】xy归纳:对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.1.如图所示,请分别画出△ABC在直角坐标系中关于y轴,x轴对称的三角形······【跟踪训练】ABCDA′B′C′D′·······2.四边形ABCD的四个顶点的坐标分别是A(-5,1),
B(-2,1),C(-2,5),D(-5,4),作出与四边形ABCD关于y轴对称的图形.·0 1 2 3 4 5 6 7 8 9 1087654321
-1-2-3-4y3.图中小鱼各顶点的横坐标保持不变,纵坐标分别乘以-1,再将所得的点用线段依次连接起来.此时,所得图案与原图案相比有什么变化?关于x轴对称x1.完成下表(-1,-2)(1,2)(-4,-3)(4, 3)(6, -7)(-6,7)(-5, 1)(5,-1)(-9,0)(9,0)2.完成下表(-2,-3)(2,3)(-1,-2)(1, 2)(6, -5)(-6, 5)(-0.5, 1)(0.5,-1)(-4,0)(4,0)4.已知点P(6, b+2)与点P ′(a+b, -3a).
若点P与点P ′关于x轴对称,则a=_____ b=_______.
若点P与点P ′关于y轴对称,则a=_____ b=_______.242-83.已知点P(6, 2)与点P ′(b, -a).
若点P与点P′关于x轴对称,则a=_____ b=_______.
若点P与点P ′关于y轴对称,则a=_____ b=_______.26-2-65.已知线段AB的两个端点的坐标分别为A(-4,1),
B(-1,4),作出线段AB关于y轴对称的图形.··A(-4,1)B(-1,4)A'(4,1)B'(1,4)【解析】点A(-4,1),B(-1,4)关于y轴对称的点的坐标分别为A′(4,1),B′ (1,4).连接A′,B′,就得到线段AB关于y轴对称的线段A′B′.··1.学习了在平面直角坐标系中关于x轴和y轴对称的点的坐标的特点.关于x轴对称的点的横坐标相等,纵坐标互为相反数.关于y轴对称的点的横坐标互为相反数,纵坐标相等.2.学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形.先求出已知图形中的一些特殊点(如多边形的顶点)的对应
点的坐标,描出并连接这些点,就可以得到这个图形的轴对
称图形. 古之立大事者,不惟有超世之才,亦必有坚忍不拔之志.
—— 苏 轼
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
