青岛版八下 第10章一次函数复习与回顾课件(共46张PPT)
文档属性
| 名称 | 青岛版八下 第10章一次函数复习与回顾课件(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:45:39 | ||
图片预览










文档简介
(共46张PPT)
一次函数回顾
正比例函数、一次
函数图象性质
正比例函数、一次函数的定义
答 案
形如 (k是常数且k≠0)的函数,叫做正比例函数,k叫做 ;
形如 (k、b是常数且k≠0)的函数,叫做一次函数.
当b=0时,一次函数y=kx+b即变为 ,所以正比例函数是一种特殊的 .
y=kx
比例系数
y=kx+b
y=kx
一次函数
笔记
例1
答 案
已知
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
(1)根据一次函数的定义,得:2-|m|=1,
解得m=±1.
又∵m+1≠0即m≠-1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,
得:2-|m|=1,n+4=0,
解得m=±1,n=-4,
又∵m+1≠0即m≠-1,
∴当m=1,n=-4时,这个函数是正比例函数.
练习1.1
答 案
(1)下列函数是一次函数,但不是正比例函数的是( )
A.y=5x B.y= x2 C.y=x-4 D.y=2x2-3
(2)若y=(m-1) +2m,y是x的一次函数,则m= .
(1) C;(2) -1.
正比例函数y=kx(k为常数,k≠0)的图象必经过 .
正比例函数的图象与性质
正比例函数、一次函数的图象性质
讲解
原点
图象(简图) 位置 增减性
k>0 图象过一、三象限 y随x增大而增大
k<0 图象过二、四象限 y随x增大而减小
注意
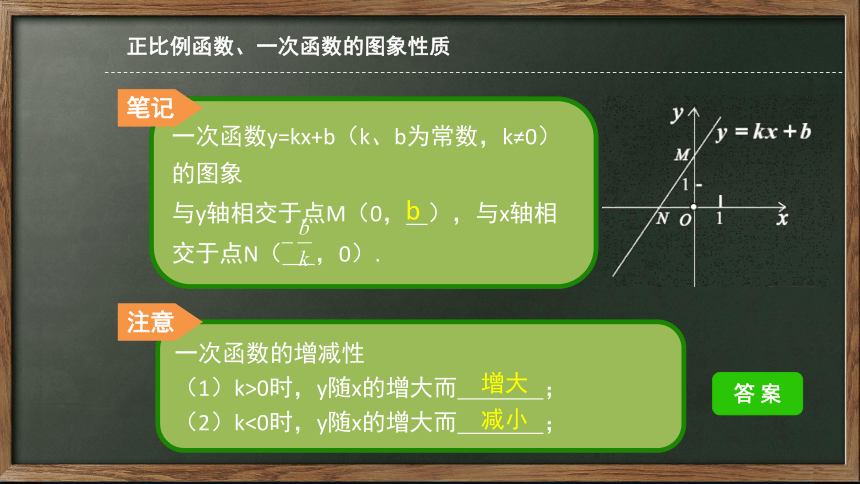
一次函数y=kx+b(k、b为常数,k≠0)的图象
与y轴相交于点M(0, ),与x轴相交于点N( ,0).
答 案
b
一次函数的增减性
(1)k>0时,y随x的增大而 ;
(2)k<0时,y随x的增大而 ;
注意
笔记
增大
减小
正比例函数、一次函数的图象性质
正比例函数、一次函数的图象性质
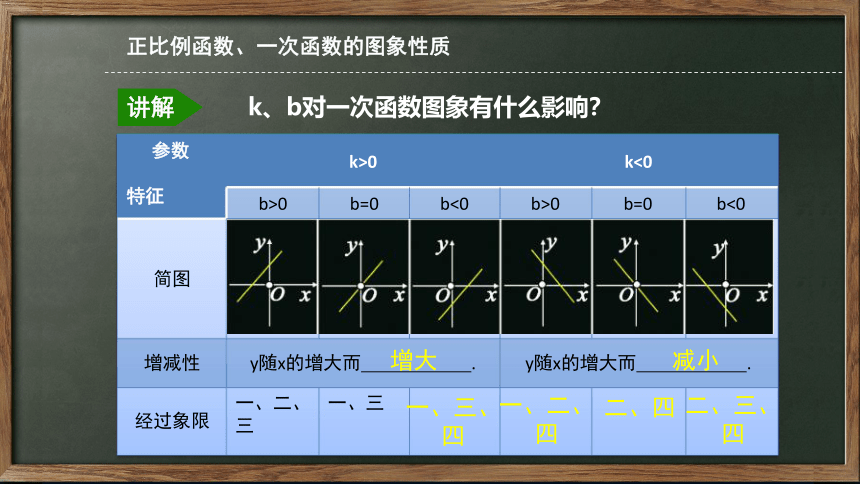
k、b对一次函数图象有什么影响?
讲解
参数
特征 k>0 k<0
b>0 b=0 b<0 b>0 b=0 b<0
简图
增减性 y随x的增大而 . y随x的增大而 .
经过象限 一、二、三 一、三
增大
减小
一、三、四
一、二、四
二、四
二、三、四
答 案
例2
(1)y=(3 - π)x图象经过 象限,y的值随x的值增大而 ;
(2)正比例函数y=kx的y值随x的增大而增大,则此函数的图象经过( )
A.一、二象限 B.一、三象限 C.二、三象限 D.二、四象限
二、四
减小
B
答 案
练习2.1
(1)对于一次函数y=kx+b(k≠0),下列说法中正确的是( )
A.若k>0,则y随着x的增大而减小
B.若b>0,则函数图象与y轴的交点位于y轴的负半轴
C.若k>0且b>0,则函数图象一定不过第四象限
D.若k<0且b<0,则函数图象一定不过第二象限
C
答 案
练习2.1
(2)已知一次函数y=x+2,则下列说法中正确的是( )
A.函数图象与x轴交于正半轴
B.函数图象与坐标轴所围成的面积为2
C.当y= - 1时,x= - 1
D.函数图象上一点A,若点A纵坐标为b,则其横坐标为b+2
B
答 案
练习2.1
(3)已知一次函数表达式y=(a+1)x+(b-2),若函数图象不经过第三象限,则a、b的取值范围是 .
a<-1,b≥2
答 案
练习2.1
(4)直线y=mx+n与直线y=mnx(mn≠0)在同一坐标中的大致图象可能是( )
A. B.
C. D.
C
一次函数解析式
一次函数求解析式
讲解
先设出解析式y=kx+b(k≠0),再根据条件确定解析式中未知参数k、b,从而得出解析式的方法叫做待定系数法.
步骤
定模型:设解析式
代条件:代入点坐标
解方程:求出k,b得解析式
答 案
【示例】已知一次函数的图象过点(1,3)与(-2,-4).用待定系数法求一次函数解析式
一次函数求解析式
解:设一次函数解析式为:
y=kx+b
将(1,3)与(-2,-4)代入得:
= +b k=
= +b b=
解析式为:y= .
3
k
-4
-2k
求解析式时第一步要根据对应函数先设出解析式,再进行计算;将点代入解析式中,注意横纵坐标.
总结
一次函数求解析式
答 案
已知正比例函数y=kx图象经过点(3,-6),求:
(1)求这个函数的解析式;
∵正比例函数y=kx经过点(3,-6),
∴-6=3·k,
解得:k=-2
∴这个正比例函数的解析式为:y=-2x;
利用待定系数法把(3,-6)代入正比例函数y=kx中计算出k即可得到解析式;
例3
解析
答 案
已知正比例函数y=kx图象经过点(3,-6),求:
(2)判断点A(4,-2)是否在这个函数图象上;
将x=4代入y=-2x得:y=-8≠-2,
∴点A(4,-2)不在这个函数图象上;
将A点的横坐标代入正比例函数关系式,计算函数值,若函数值等于-2,则A点在这个函数图象上,否则不在这个函数图象上;
例3
解析
已知正比例函数y=kx图象经过点(3,-6),求:
(3)图象上两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
∵k=-2<0
∴y随x的增大而减小
∵x1>x2
∴y1
根据正比例函数的性质:当k<0时,y随x的增大而减小,即可判断.
答 案
例3
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(1)求直线AB的函数表达式;
练习3.1
这直线的表达式为y=kx+b,
把点A、B的坐标代入得:
-k+b=5
3k+b=-3
解得:k=-2,b=3
所以直线表达式为y=-2x+3;
设直线的表达式为y=kx+b,把点A、B的坐标代入求出k、b,即可得出答案;
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(2)求a的值;
练习3.1
把P(2,a)代入y=-2x+3得:
a=-2×2+3
a=-1;
把P点的坐标代入求出即可;
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(3)求△AOP的面积;
练习3.1
根据坐标和三角形面积公式求出即可;
解析
∵把x=0代入y=-2x+3得:y=3,
∴直线y=-2x+3与y轴的交点D的坐标(0,3),即OD=3,
∵P(2,-1)
∴△AOP的面积=△AOD的面积+△DOP的面积
=
答 案
一次函数y=kx+b,当1y=2x-5或y=-2x+5
例4
答 案
已知一次函数y=kx+b,当-3≤x≤1时,对应y的值为1≤y≤9,则k+b的值为 .
9或1
练习4.1
一次函数的交点
答 案
【示例1】求y=2x+1与坐标轴的交点.
分析:求与x轴交点,令y=0,则x= ,则交点
为 .
求与y轴交点,令x=0,则y= ,则交点为 .
1
(0,1)
【示例2】已知P是一次函数y=2x+3和y=-2x图像的交点,如何求点P的坐标呢?
分析:因为交点既在y=2x+3又在y=-2x上,所以要联立解析式,得方程求解,
联立解析式,得到方程组:
解得:x= .
y= .
则 为两函数交点.
y=2x+3
.
一次函数的交点
答 案
y=-2x
( , )
如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析式;
(3)求△ADC的面积
例5
解(1)当y=-3x+3=0时,x=1
∴D(1,0)
解:(2)设直线l2的解析式为y=kx+b(k≠0),
把A(4,0)、B(3,- )代入表达式 y=kx+b,
4k+b=0 ,解得: k= ,
3k+b= b=-6
∴直线l2的解析式为y= x-6
(3)联立y=-3x+3和y= x-6,
解得:x=2,y=3,∴C(2,-3),
∴S△ADC=
例5
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOD的面积
练习5.1
解:(1)将A(m,2)代入y=2x,得:
2=2m,则m=1,
将A(1,2)和B(-2,-1)代入y=kx+b中,
得: k+b=2 解得: k=1
-2k+b=-1 b=1
则解析式为y=x+1;
(2)在y=x+1中,当x=0时,y=1,
则C点的坐标为(0,1).
(3)当y=0时,x=-1,即OD=1,
∴S△AOD=?×1×2=1
练习5.1
一次函数的平移
【示例】一次函数y=2x+3向右平移3个单位,求平移后直线解析式.
分析:
3
一次函数平移
A(0, )B( ,0),
A'(3, )B'( ,0),
设y=kx+b
3k+b= . k= .
k+b=0 b= .
解析式为 .
在原函数上任取两个点A、B;
将点A、B按要求变换得到A'、B'
待定系数法求新解析式
3
3
2
-3
y=2x-3
答 案
一次函数平移
平移变换口诀:
(1)上下平移口诀: .
直线y=kx+b向上平移m个单位: .
向下平移m个单位: .
(2)左右平移口诀: .
直线y=kx+b向左平移m个单位: .
向右平移m个单位: .
总结
把y上加下减
把x左加右减
y=kx+b+m
y=kx+b-m
y=k(x+m)+b
y=k(x-m)+b
答 案
(1)对于直线:y=2x-1,
①求向下平移4个单位后的解析式;
②求向右平移2个单位后的解析式;
③求先向左平移3个单位,再向上平移1个单位后的解析式.
①y=2x-5;②y=2x-5;③y=2x+6
例6
解析
①y=2x-1-4;
②y=2(x-2)-1;
③y=2(x+3)-1+1
答 案
(2)若直线y=kx+b的图象向上平移3个单位,再向左平移1个单位,平移后的直线的函数解析式为y=2x+5,求k、b.
k=2,b=0
例6
解析
由题意知y=k(x+1)+b+3=2x+5
得 kx=2x
b+3+k=5
可求出k、b的值
答 案
(3)若一次函数y=kx+b的图象向左平移3个单位,再向上平移2个单位,平移后的图象与原图象重合,你能确定k、b的值吗?
例6
解析
k= ,不能确定b的值
kx+b+3=k(x+3)+b+2
3k+2=0
解得k=
答 案
(1)对于直线:y=-3x+2.
①将该直线向左平移1个单位后得到的直线的解析式为
.
②将该直线向上平移5个单位后得到的直线的解析式为
.
①将该直线向右平移2个单位,再向下平移3个单位后得到的直线的解析式为 .
①y=-3x-1
②y=-3x+7
③y=-3x+5
练习6.1
答 案
(2)若直线y=mx+n的图象先向左平移1个单位,再向下平移2个单位,平移后直线的函数解析式为y=3x-2,
则m= ,n= .
m=3,n=-3
练习6.1
(3)若一次函数y=kx+1的图象向左平移2个单位,再向下平移2个单位,平移后的图象与原图象重合,
则k= .
k=1
答 案
一次函数的对称
A(0,3)B(-1,1),
A'( )B'( ),
设y=kx+b
b=-3. k= .
-k+b=-1 b= .
解析式为 .
【示例】一次函数y=2x+3关于x轴对称后,求平移后直线解析式.
分析:
一次函数对称
在原函数上任取两个点A、B;
结合图形求出对称点后,直线上另个点坐标A'、B'
待定系数法求对称后的解析式
0,-3
-2
-3
y=-2x-3
-1,-1
一次函数平移
对称变换口诀:直线y=kx+b
(1)关于x轴对称变为:-y=kx+b y=-kx-b
(2)关于y轴对称变为: y=-kx+b
(3)关于原点中心对称变为: -y=-kx+b y=kx-b
总结
(1)求一次函数解析式y=x-1的图象关于x轴对称的函数解析式;
(2)求一次函数解析式y=3x-1的图象关于y轴对称的函数解析式;
(3)求一次函数解析式y=-2x-1的图象关于原点对称的函数解析式;
答 案
y=-x+1;
例7
答 案
y=-3x-1;
y=-2x+1;
答 案
(1)一次函数y=-2x+3的图象关于x轴对称直线的函数解析式为 ;
(2)一次函数y=-x+2的图象关于y轴对称直线的函数解析式为 ;
(3)一次函数y=x-37的图象关于原点对称直线的函数解析式为 ;
答 案
y=2x-3;
练习7.1
答 案
y=x+2;
y=x+3;
答 案
Thank you
一次函数回顾
正比例函数、一次
函数图象性质
正比例函数、一次函数的定义
答 案
形如 (k是常数且k≠0)的函数,叫做正比例函数,k叫做 ;
形如 (k、b是常数且k≠0)的函数,叫做一次函数.
当b=0时,一次函数y=kx+b即变为 ,所以正比例函数是一种特殊的 .
y=kx
比例系数
y=kx+b
y=kx
一次函数
笔记
例1
答 案
已知
(1)当m、n取何值时,y是x的一次函数?
(2)当m、n取何值时,y是x的正比例函数?
(1)根据一次函数的定义,得:2-|m|=1,
解得m=±1.
又∵m+1≠0即m≠-1,
∴当m=1,n为任意实数时,这个函数是一次函数;
(2)根据正比例函数的定义,
得:2-|m|=1,n+4=0,
解得m=±1,n=-4,
又∵m+1≠0即m≠-1,
∴当m=1,n=-4时,这个函数是正比例函数.
练习1.1
答 案
(1)下列函数是一次函数,但不是正比例函数的是( )
A.y=5x B.y= x2 C.y=x-4 D.y=2x2-3
(2)若y=(m-1) +2m,y是x的一次函数,则m= .
(1) C;(2) -1.
正比例函数y=kx(k为常数,k≠0)的图象必经过 .
正比例函数的图象与性质
正比例函数、一次函数的图象性质
讲解
原点
图象(简图) 位置 增减性
k>0 图象过一、三象限 y随x增大而增大
k<0 图象过二、四象限 y随x增大而减小
注意
一次函数y=kx+b(k、b为常数,k≠0)的图象
与y轴相交于点M(0, ),与x轴相交于点N( ,0).
答 案
b
一次函数的增减性
(1)k>0时,y随x的增大而 ;
(2)k<0时,y随x的增大而 ;
注意
笔记
增大
减小
正比例函数、一次函数的图象性质
正比例函数、一次函数的图象性质
k、b对一次函数图象有什么影响?
讲解
参数
特征 k>0 k<0
b>0 b=0 b<0 b>0 b=0 b<0
简图
增减性 y随x的增大而 . y随x的增大而 .
经过象限 一、二、三 一、三
增大
减小
一、三、四
一、二、四
二、四
二、三、四
答 案
例2
(1)y=(3 - π)x图象经过 象限,y的值随x的值增大而 ;
(2)正比例函数y=kx的y值随x的增大而增大,则此函数的图象经过( )
A.一、二象限 B.一、三象限 C.二、三象限 D.二、四象限
二、四
减小
B
答 案
练习2.1
(1)对于一次函数y=kx+b(k≠0),下列说法中正确的是( )
A.若k>0,则y随着x的增大而减小
B.若b>0,则函数图象与y轴的交点位于y轴的负半轴
C.若k>0且b>0,则函数图象一定不过第四象限
D.若k<0且b<0,则函数图象一定不过第二象限
C
答 案
练习2.1
(2)已知一次函数y=x+2,则下列说法中正确的是( )
A.函数图象与x轴交于正半轴
B.函数图象与坐标轴所围成的面积为2
C.当y= - 1时,x= - 1
D.函数图象上一点A,若点A纵坐标为b,则其横坐标为b+2
B
答 案
练习2.1
(3)已知一次函数表达式y=(a+1)x+(b-2),若函数图象不经过第三象限,则a、b的取值范围是 .
a<-1,b≥2
答 案
练习2.1
(4)直线y=mx+n与直线y=mnx(mn≠0)在同一坐标中的大致图象可能是( )
A. B.
C. D.
C
一次函数解析式
一次函数求解析式
讲解
先设出解析式y=kx+b(k≠0),再根据条件确定解析式中未知参数k、b,从而得出解析式的方法叫做待定系数法.
步骤
定模型:设解析式
代条件:代入点坐标
解方程:求出k,b得解析式
答 案
【示例】已知一次函数的图象过点(1,3)与(-2,-4).用待定系数法求一次函数解析式
一次函数求解析式
解:设一次函数解析式为:
y=kx+b
将(1,3)与(-2,-4)代入得:
= +b k=
= +b b=
解析式为:y= .
3
k
-4
-2k
求解析式时第一步要根据对应函数先设出解析式,再进行计算;将点代入解析式中,注意横纵坐标.
总结
一次函数求解析式
答 案
已知正比例函数y=kx图象经过点(3,-6),求:
(1)求这个函数的解析式;
∵正比例函数y=kx经过点(3,-6),
∴-6=3·k,
解得:k=-2
∴这个正比例函数的解析式为:y=-2x;
利用待定系数法把(3,-6)代入正比例函数y=kx中计算出k即可得到解析式;
例3
解析
答 案
已知正比例函数y=kx图象经过点(3,-6),求:
(2)判断点A(4,-2)是否在这个函数图象上;
将x=4代入y=-2x得:y=-8≠-2,
∴点A(4,-2)不在这个函数图象上;
将A点的横坐标代入正比例函数关系式,计算函数值,若函数值等于-2,则A点在这个函数图象上,否则不在这个函数图象上;
例3
解析
已知正比例函数y=kx图象经过点(3,-6),求:
(3)图象上两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
∵k=-2<0
∴y随x的增大而减小
∵x1>x2
∴y1
根据正比例函数的性质:当k<0时,y随x的增大而减小,即可判断.
答 案
例3
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(1)求直线AB的函数表达式;
练习3.1
这直线的表达式为y=kx+b,
把点A、B的坐标代入得:
-k+b=5
3k+b=-3
解得:k=-2,b=3
所以直线表达式为y=-2x+3;
设直线的表达式为y=kx+b,把点A、B的坐标代入求出k、b,即可得出答案;
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(2)求a的值;
练习3.1
把P(2,a)代入y=-2x+3得:
a=-2×2+3
a=-1;
把P点的坐标代入求出即可;
解析
答 案
在直角坐标系中,一条直线经过A(-1,5),P(2,a),B(3,-3).
(3)求△AOP的面积;
练习3.1
根据坐标和三角形面积公式求出即可;
解析
∵把x=0代入y=-2x+3得:y=3,
∴直线y=-2x+3与y轴的交点D的坐标(0,3),即OD=3,
∵P(2,-1)
∴△AOP的面积=△AOD的面积+△DOP的面积
=
答 案
一次函数y=kx+b,当1
例4
答 案
已知一次函数y=kx+b,当-3≤x≤1时,对应y的值为1≤y≤9,则k+b的值为 .
9或1
练习4.1
一次函数的交点
答 案
【示例1】求y=2x+1与坐标轴的交点.
分析:求与x轴交点,令y=0,则x= ,则交点
为 .
求与y轴交点,令x=0,则y= ,则交点为 .
1
(0,1)
【示例2】已知P是一次函数y=2x+3和y=-2x图像的交点,如何求点P的坐标呢?
分析:因为交点既在y=2x+3又在y=-2x上,所以要联立解析式,得方程求解,
联立解析式,得到方程组:
解得:x= .
y= .
则 为两函数交点.
y=2x+3
.
一次函数的交点
答 案
y=-2x
( , )
如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析式;
(3)求△ADC的面积
例5
解(1)当y=-3x+3=0时,x=1
∴D(1,0)
解:(2)设直线l2的解析式为y=kx+b(k≠0),
把A(4,0)、B(3,- )代入表达式 y=kx+b,
4k+b=0 ,解得: k= ,
3k+b= b=-6
∴直线l2的解析式为y= x-6
(3)联立y=-3x+3和y= x-6,
解得:x=2,y=3,∴C(2,-3),
∴S△ADC=
例5
如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,-1),与y轴的交点为C,与x轴的交点为D.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOD的面积
练习5.1
解:(1)将A(m,2)代入y=2x,得:
2=2m,则m=1,
将A(1,2)和B(-2,-1)代入y=kx+b中,
得: k+b=2 解得: k=1
-2k+b=-1 b=1
则解析式为y=x+1;
(2)在y=x+1中,当x=0时,y=1,
则C点的坐标为(0,1).
(3)当y=0时,x=-1,即OD=1,
∴S△AOD=?×1×2=1
练习5.1
一次函数的平移
【示例】一次函数y=2x+3向右平移3个单位,求平移后直线解析式.
分析:
3
一次函数平移
A(0, )B( ,0),
A'(3, )B'( ,0),
设y=kx+b
3k+b= . k= .
k+b=0 b= .
解析式为 .
在原函数上任取两个点A、B;
将点A、B按要求变换得到A'、B'
待定系数法求新解析式
3
3
2
-3
y=2x-3
答 案
一次函数平移
平移变换口诀:
(1)上下平移口诀: .
直线y=kx+b向上平移m个单位: .
向下平移m个单位: .
(2)左右平移口诀: .
直线y=kx+b向左平移m个单位: .
向右平移m个单位: .
总结
把y上加下减
把x左加右减
y=kx+b+m
y=kx+b-m
y=k(x+m)+b
y=k(x-m)+b
答 案
(1)对于直线:y=2x-1,
①求向下平移4个单位后的解析式;
②求向右平移2个单位后的解析式;
③求先向左平移3个单位,再向上平移1个单位后的解析式.
①y=2x-5;②y=2x-5;③y=2x+6
例6
解析
①y=2x-1-4;
②y=2(x-2)-1;
③y=2(x+3)-1+1
答 案
(2)若直线y=kx+b的图象向上平移3个单位,再向左平移1个单位,平移后的直线的函数解析式为y=2x+5,求k、b.
k=2,b=0
例6
解析
由题意知y=k(x+1)+b+3=2x+5
得 kx=2x
b+3+k=5
可求出k、b的值
答 案
(3)若一次函数y=kx+b的图象向左平移3个单位,再向上平移2个单位,平移后的图象与原图象重合,你能确定k、b的值吗?
例6
解析
k= ,不能确定b的值
kx+b+3=k(x+3)+b+2
3k+2=0
解得k=
答 案
(1)对于直线:y=-3x+2.
①将该直线向左平移1个单位后得到的直线的解析式为
.
②将该直线向上平移5个单位后得到的直线的解析式为
.
①将该直线向右平移2个单位,再向下平移3个单位后得到的直线的解析式为 .
①y=-3x-1
②y=-3x+7
③y=-3x+5
练习6.1
答 案
(2)若直线y=mx+n的图象先向左平移1个单位,再向下平移2个单位,平移后直线的函数解析式为y=3x-2,
则m= ,n= .
m=3,n=-3
练习6.1
(3)若一次函数y=kx+1的图象向左平移2个单位,再向下平移2个单位,平移后的图象与原图象重合,
则k= .
k=1
答 案
一次函数的对称
A(0,3)B(-1,1),
A'( )B'( ),
设y=kx+b
b=-3. k= .
-k+b=-1 b= .
解析式为 .
【示例】一次函数y=2x+3关于x轴对称后,求平移后直线解析式.
分析:
一次函数对称
在原函数上任取两个点A、B;
结合图形求出对称点后,直线上另个点坐标A'、B'
待定系数法求对称后的解析式
0,-3
-2
-3
y=-2x-3
-1,-1
一次函数平移
对称变换口诀:直线y=kx+b
(1)关于x轴对称变为:-y=kx+b y=-kx-b
(2)关于y轴对称变为: y=-kx+b
(3)关于原点中心对称变为: -y=-kx+b y=kx-b
总结
(1)求一次函数解析式y=x-1的图象关于x轴对称的函数解析式;
(2)求一次函数解析式y=3x-1的图象关于y轴对称的函数解析式;
(3)求一次函数解析式y=-2x-1的图象关于原点对称的函数解析式;
答 案
y=-x+1;
例7
答 案
y=-3x-1;
y=-2x+1;
答 案
(1)一次函数y=-2x+3的图象关于x轴对称直线的函数解析式为 ;
(2)一次函数y=-x+2的图象关于y轴对称直线的函数解析式为 ;
(3)一次函数y=x-37的图象关于原点对称直线的函数解析式为 ;
答 案
y=2x-3;
练习7.1
答 案
y=x+2;
y=x+3;
答 案
Thank you
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
