2020湘教版八下数学4.5一次函数的应用第1课时习题课件(34张PPT)
文档属性
| 名称 | 2020湘教版八下数学4.5一次函数的应用第1课时习题课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 821.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览











文档简介
课件34张PPT。4.5 一次函数的应用?
第1课时1.能通过函数图象获取信息,进一步提高识图能力.(重点)
2.能利用一次函数解决简单的实际问题,进一步发展数学应用能力.(难点)1.根据函数图象判断函数类型:图象是直线,则函数是一次函数;
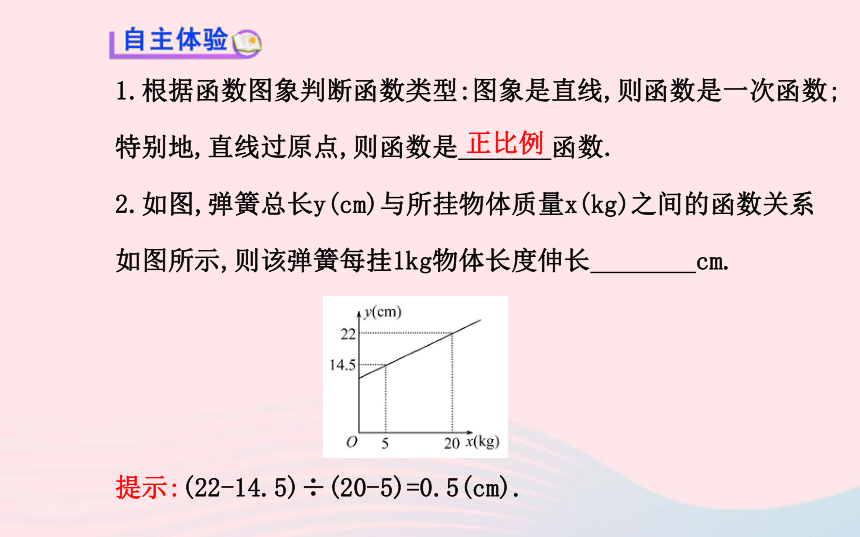
特别地,直线过原点,则函数是_______函数.
2.如图,弹簧总长y(cm)与所挂物体质量x(kg)之间的函数关系
如图所示,则该弹簧每挂1kg物体长度伸长 cm.
提示:(22-14.5)÷(20-5)=0.5(cm).正比例3.某人骑摩托车由天津驶往相距120km的北京,s(km)表示摩托车行驶的路程如图所示:
(1)摩托车4 h可从天津到北京,速度是________.
(2)若摩托车行驶了1 h,则离开天津___km.30 km/h30【总结】从图象中获取信息可以从两个方面去分析图象:
(1)从函数图象是否过原点可以判断函数的类型.
(2)从x轴、y轴的实际意义去理解图象上点的坐标的实际意义,通过观察点的位置去寻找所需要的信息. (打“√”或“×”)
(1)利用一次函数解决实际问题时,一定要把函数图象画完整.
( )
(2)利用函数解决实际问题时,不需要考虑自变量的取值范围.
( )
(3)在一边(矩形的长)靠墙(墙长20m)的地方围建一个矩形的养
鸡场,另三边用竹篱笆围成,如果竹篱笆总长为18m,鸡舍的宽
y(m)与长x(m)的函数表达式为y=9-0.5x. ( )××√知识点 一次函数的实际应用?
【例】小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)小丽驾车的最高速度是 km/h.
(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度.(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?【思路点拨】(1)观察函数图象可得最高速度.
(2)分别确定点C,点D的坐标,用待定系数法求直线CD的函数表达式,当自变量为22时,求相应函数值.
(3)利用所给公式求出各时间段所行驶的路程之和,再乘每百千米油耗即可.【自主解答】(1)60.
(2)当20≤x≤30时,设y与x之间的函数表达式为y=kx+b(k,b
为常数,k≠0).
根据题意,当x=20时,y=60;
当x=30时,y=24.
所以 解得
所以y与x之间的函数表达式为y=-3.6x+132.
当x=22时,y=-3.6×22+132=52.8.
所以,小丽出发第22 min时的速度为52.8 km/h. (3)小丽驾车从甲地到乙地行驶的路程为
所以,小丽驾车从甲地到乙地共耗油为33.5× =3.35(L).【总结提升】利用函数图象解决实际问题的步骤及注意事项
1.五个步骤:
(1)分析题目中的已知条件,找出题目中的相关关系.
(2)确定函数的类型,设出相应的表达式.
(3)将相关条件代入表达式,并求解.
(4)根据题意写出函数表达式并画出图象.
(5)根据函数图象的性质和自变量的值的情况对问题作出结论.2.三个注意:
(1)实际问题中要注意使实际问题有意义,同时要注意自变量的取值范围.
(2)当问题涉及多种情况时,要注意分类讨论.
(3)利用图象解题时,要弄清横坐标和纵坐标各自的实际意义.题组:一次函数的实际应用
1.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为 ( )
A.20 kg B.25 kg C.28 kg D.30 kg【解析】选A.设y与x之间的函数表达式为y=kx+b(k,b为常数,k≠0),
由题意可知
所以k=30,b=-600,
所以函数表达式为y=30x-600,
当y=0时,即30x-600=0,所以x=20.2.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(min)之间的函数关系,则通话8min应付电话费 元.【解析】由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的表达式为y=kt+b(k,b为常数,k≠0)(t≥3),
则 解得
所以,射线BC的表达式为y=t-0.6(t≥3),
当t=8时,y=8-0.6=7.4(元).
答案:7.43.某水果店为了尽快销售一种水果,按以下方法进行促销:购买这种水果不超过10kg的,每千克a元;超过10kg的,超出部分每千克c元.某人两次到该店购买这种水果的质量x(kg)与付款y(元)如下表:
(1)求a,c的值,并写出当0≤x≤10和x>10时,y与x之间的函数表达式.
(2)若购买这种水果75kg,应付款多少元?【解析】(1)把x=10,y=30代入y=ax(a≠0),
得30=a×10,解得a=3.
把x=15,y=43代入y=30+(15-10)c,解得c=2.6,
y与x之间的函数表达式分别为y=3x(0≤x≤10);
y=2.6(x-10)+30,即y=2.6x+4(x>10).
(2)把x=75代入y=2.6x+4中,得y=199.
答:购买这种水果75kg,应付款199元.4.某生物小组观察一
植物生长,得到植物高度y(单位:cm)与
观察时间x(单位:天)的关系,并画出图
象(AC是线段,直线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的表达式,并求该植物最高时长了多少cm?【解析】(1)根据图象可知,该植物从观察时起50天后停止长高.
(2)设AC的函数表达式是y=kx+b(k,b为常数,k≠0),则
解得
∴AC的函数表达式是
当x=50时,
∴该植物最高时长了10 cm.5.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长的对应数值:
(1)分析上表,“鞋码”与鞋长之间的关系符合你学过的哪种函数关系?
(2)设鞋长为x,“鞋码”为y,求y与x之间的函数表达式.
(3)如果你需要的鞋长为26cm,那么应该买多大码的鞋?【解析】(1)根据表中信息得“鞋码”与鞋长之间的关系是一
次函数关系.
(2)设一次函数的表达式为y=kx+b(k,b为常数,k≠0),
则由题意得 解得:
∴y=2x-10.
(3)x=26时,y=2×26-10=42.
答:应该买42码的鞋.6.星期天8:00~8:30,燃气公司给平安加气
站的储气罐注入天然气.之后,一位工作人员
以每车20立方米的加气量,依次给在加气站
排队等候的若干辆车加气.储气罐中的储气
量y(m3)与时间x(h)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?
(2)当x≥0.5时,求储气罐中的储气量y(m3)与时间x(h)之间的函数表达式.(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
【解析】(1)由图可知,星期天当日注入了10000-2000=8000m3的天然气.(2)当x≥0.5时,设储气罐中的储气量y(m3)与时间x(h)之间的函数表达式为:y=kx+b(k,b为常数,且k≠0),
∵图象过点(0.5,10 000),(10.5,8 000),
∴ 解得
故所求函数表达式为:y=-200x+10 100.(3)可以.
∵给18辆车加气需18×20=360(m3),储气量为10000-360=
9640(m3),
于是有:9640=-200x+10100,解得x=2.3,
而从8:00到10:30相差2.5h,显然有:2.3<2.5,故第18辆车在当天10:30之前可以加完气.7.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)乙队开挖到30m时,用了 h.开挖6h时,甲队比乙队多挖了 m.
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数表达式;
②乙队在2≤x≤6的时段内,y与x之间的函数表达式.
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?【解析】(1)依题意得乙队开挖到30 m时,用了2 h,开挖6 h时,甲队比乙队多挖了60-50=10(m).(2)①设甲队在0≤x≤6的时段内y与x之间的函数表达式为
y=k1x(k1为常数,k1≠0),由图可知,函数图象过点(6,60),
∴6k1=60,解得k1=10,∴y=10x.
②设乙队在2≤x≤6的时段内y与x之间的函数表达式为
y=k2x+b(k2,b为常数,k2≠0),由图可知,函数图象过点(2,
30),(6,50),∴ 解得
∴y=5x+20.(3)由题意,得10x=5x+20,解得x=4(h).
∴当x为4 h时,甲、乙两队所挖的河渠长度相等.【想一想错在哪?】某班同学在研究弹簧的长度跟外力的变化关系时,实验记录了得到的相应数据如下
则y关于x的函数图象是 ( )提示:应通过表格计算得出正确答案,因弹簧具有一定的弹性限度.
第1课时1.能通过函数图象获取信息,进一步提高识图能力.(重点)
2.能利用一次函数解决简单的实际问题,进一步发展数学应用能力.(难点)1.根据函数图象判断函数类型:图象是直线,则函数是一次函数;
特别地,直线过原点,则函数是_______函数.
2.如图,弹簧总长y(cm)与所挂物体质量x(kg)之间的函数关系
如图所示,则该弹簧每挂1kg物体长度伸长 cm.
提示:(22-14.5)÷(20-5)=0.5(cm).正比例3.某人骑摩托车由天津驶往相距120km的北京,s(km)表示摩托车行驶的路程如图所示:
(1)摩托车4 h可从天津到北京,速度是________.
(2)若摩托车行驶了1 h,则离开天津___km.30 km/h30【总结】从图象中获取信息可以从两个方面去分析图象:
(1)从函数图象是否过原点可以判断函数的类型.
(2)从x轴、y轴的实际意义去理解图象上点的坐标的实际意义,通过观察点的位置去寻找所需要的信息. (打“√”或“×”)
(1)利用一次函数解决实际问题时,一定要把函数图象画完整.
( )
(2)利用函数解决实际问题时,不需要考虑自变量的取值范围.
( )
(3)在一边(矩形的长)靠墙(墙长20m)的地方围建一个矩形的养
鸡场,另三边用竹篱笆围成,如果竹篱笆总长为18m,鸡舍的宽
y(m)与长x(m)的函数表达式为y=9-0.5x. ( )××√知识点 一次函数的实际应用?
【例】小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)小丽驾车的最高速度是 km/h.
(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度.(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?【思路点拨】(1)观察函数图象可得最高速度.
(2)分别确定点C,点D的坐标,用待定系数法求直线CD的函数表达式,当自变量为22时,求相应函数值.
(3)利用所给公式求出各时间段所行驶的路程之和,再乘每百千米油耗即可.【自主解答】(1)60.
(2)当20≤x≤30时,设y与x之间的函数表达式为y=kx+b(k,b
为常数,k≠0).
根据题意,当x=20时,y=60;
当x=30时,y=24.
所以 解得
所以y与x之间的函数表达式为y=-3.6x+132.
当x=22时,y=-3.6×22+132=52.8.
所以,小丽出发第22 min时的速度为52.8 km/h. (3)小丽驾车从甲地到乙地行驶的路程为
所以,小丽驾车从甲地到乙地共耗油为33.5× =3.35(L).【总结提升】利用函数图象解决实际问题的步骤及注意事项
1.五个步骤:
(1)分析题目中的已知条件,找出题目中的相关关系.
(2)确定函数的类型,设出相应的表达式.
(3)将相关条件代入表达式,并求解.
(4)根据题意写出函数表达式并画出图象.
(5)根据函数图象的性质和自变量的值的情况对问题作出结论.2.三个注意:
(1)实际问题中要注意使实际问题有意义,同时要注意自变量的取值范围.
(2)当问题涉及多种情况时,要注意分类讨论.
(3)利用图象解题时,要弄清横坐标和纵坐标各自的实际意义.题组:一次函数的实际应用
1.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为 ( )
A.20 kg B.25 kg C.28 kg D.30 kg【解析】选A.设y与x之间的函数表达式为y=kx+b(k,b为常数,k≠0),
由题意可知
所以k=30,b=-600,
所以函数表达式为y=30x-600,
当y=0时,即30x-600=0,所以x=20.2.如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(min)之间的函数关系,则通话8min应付电话费 元.【解析】由图象可得,点B(3,2.4),C(5,4.4),
设射线BC的表达式为y=kt+b(k,b为常数,k≠0)(t≥3),
则 解得
所以,射线BC的表达式为y=t-0.6(t≥3),
当t=8时,y=8-0.6=7.4(元).
答案:7.43.某水果店为了尽快销售一种水果,按以下方法进行促销:购买这种水果不超过10kg的,每千克a元;超过10kg的,超出部分每千克c元.某人两次到该店购买这种水果的质量x(kg)与付款y(元)如下表:
(1)求a,c的值,并写出当0≤x≤10和x>10时,y与x之间的函数表达式.
(2)若购买这种水果75kg,应付款多少元?【解析】(1)把x=10,y=30代入y=ax(a≠0),
得30=a×10,解得a=3.
把x=15,y=43代入y=30+(15-10)c,解得c=2.6,
y与x之间的函数表达式分别为y=3x(0≤x≤10);
y=2.6(x-10)+30,即y=2.6x+4(x>10).
(2)把x=75代入y=2.6x+4中,得y=199.
答:购买这种水果75kg,应付款199元.4.某生物小组观察一
植物生长,得到植物高度y(单位:cm)与
观察时间x(单位:天)的关系,并画出图
象(AC是线段,直线CD平行于x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的表达式,并求该植物最高时长了多少cm?【解析】(1)根据图象可知,该植物从观察时起50天后停止长高.
(2)设AC的函数表达式是y=kx+b(k,b为常数,k≠0),则
解得
∴AC的函数表达式是
当x=50时,
∴该植物最高时长了10 cm.5.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长的对应数值:
(1)分析上表,“鞋码”与鞋长之间的关系符合你学过的哪种函数关系?
(2)设鞋长为x,“鞋码”为y,求y与x之间的函数表达式.
(3)如果你需要的鞋长为26cm,那么应该买多大码的鞋?【解析】(1)根据表中信息得“鞋码”与鞋长之间的关系是一
次函数关系.
(2)设一次函数的表达式为y=kx+b(k,b为常数,k≠0),
则由题意得 解得:
∴y=2x-10.
(3)x=26时,y=2×26-10=42.
答:应该买42码的鞋.6.星期天8:00~8:30,燃气公司给平安加气
站的储气罐注入天然气.之后,一位工作人员
以每车20立方米的加气量,依次给在加气站
排队等候的若干辆车加气.储气罐中的储气
量y(m3)与时间x(h)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?
(2)当x≥0.5时,求储气罐中的储气量y(m3)与时间x(h)之间的函数表达式.(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
【解析】(1)由图可知,星期天当日注入了10000-2000=8000m3的天然气.(2)当x≥0.5时,设储气罐中的储气量y(m3)与时间x(h)之间的函数表达式为:y=kx+b(k,b为常数,且k≠0),
∵图象过点(0.5,10 000),(10.5,8 000),
∴ 解得
故所求函数表达式为:y=-200x+10 100.(3)可以.
∵给18辆车加气需18×20=360(m3),储气量为10000-360=
9640(m3),
于是有:9640=-200x+10100,解得x=2.3,
而从8:00到10:30相差2.5h,显然有:2.3<2.5,故第18辆车在当天10:30之前可以加完气.7.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)乙队开挖到30m时,用了 h.开挖6h时,甲队比乙队多挖了 m.
(2)请你求出:
①甲队在0≤x≤6的时段内,y与x之间的函数表达式;
②乙队在2≤x≤6的时段内,y与x之间的函数表达式.
(3)当x为何值时,甲、乙两队在施工过程中所挖河渠的长度相等?【解析】(1)依题意得乙队开挖到30 m时,用了2 h,开挖6 h时,甲队比乙队多挖了60-50=10(m).(2)①设甲队在0≤x≤6的时段内y与x之间的函数表达式为
y=k1x(k1为常数,k1≠0),由图可知,函数图象过点(6,60),
∴6k1=60,解得k1=10,∴y=10x.
②设乙队在2≤x≤6的时段内y与x之间的函数表达式为
y=k2x+b(k2,b为常数,k2≠0),由图可知,函数图象过点(2,
30),(6,50),∴ 解得
∴y=5x+20.(3)由题意,得10x=5x+20,解得x=4(h).
∴当x为4 h时,甲、乙两队所挖的河渠长度相等.【想一想错在哪?】某班同学在研究弹簧的长度跟外力的变化关系时,实验记录了得到的相应数据如下
则y关于x的函数图象是 ( )提示:应通过表格计算得出正确答案,因弹簧具有一定的弹性限度.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
