2020湘教版八下数学第4章一次函数阶段专题复习习题课件(38张PPT)
文档属性
| 名称 | 2020湘教版八下数学第4章一次函数阶段专题复习习题课件(38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 615.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览










文档简介
课件38张PPT。阶段专题复习
第 4 章请写出框图中数字处的内容:
①__________________________________________________
____________________________________________________;
②_______________________;
③____________________________________________;
④___________________;一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么我们称y是x的函数图象法、列表法、公式法形如y=kx(k是常数,k≠0)的函数,叫做正比例函数经过原点的一条直线⑤___________________________________________________
________________;
⑥______________________________________________;
⑦_________;
⑧___________________________________________________
________________.当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数一条直线当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小考点 1 分析函数图象解决问题?
【知识点睛】
日常生活中一些不方便使用表达式表示的问题,用图象能简明清晰地反映其意义.分析图象获取信息是中考的热点,这类问题常与生活中的一些热点问题结合,难度不大,多以选择题、填空题为主,其作用在于结合问题的实际背景加深对图象意义的理解.【例1】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州.若该轮船从万州出发后所用的时间为x(h),轮船距万州的距离为y(km),则下列各图形中,能够反映y与x之间函数关系的大致图象是 ( )【思路点拨】将实际问题与函数图象结合起来,分段看图象:
①逆水行驶;②静止不动;③顺水行驶,结合图象判断.
【自主解答】选C.①逆水行驶,y随x的增大而缓慢增大;
②静止不动,y随x的增加不变;
③顺水行驶,y随x的增大快速减小.
结合图象,可得C选项正确.【中考集训】
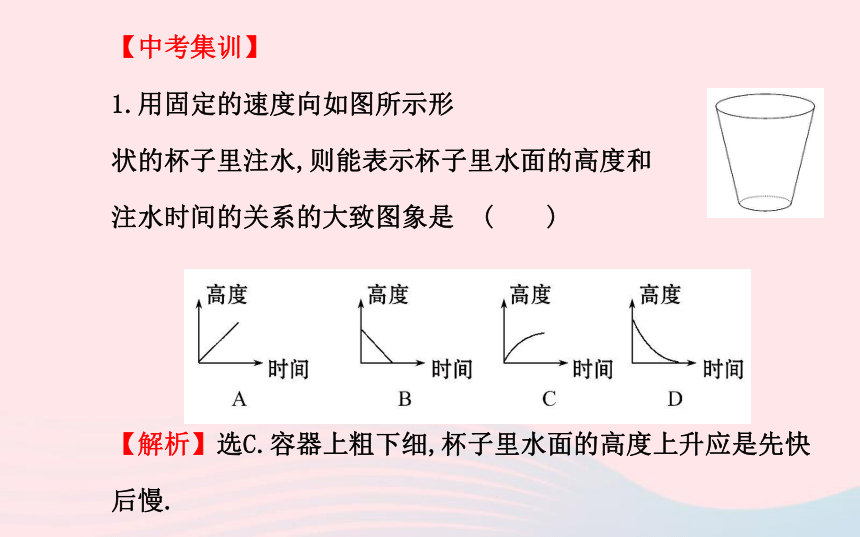
1.用固定的速度向如图所示形
状的杯子里注水,则能表示杯子里水面的高度和
注水时间的关系的大致图象是 ( )
【解析】选C.容器上粗下细,杯子里水面的高度上升应是先快后慢.2.如图,正方形ABCD的边长
为4,P为正方形边上一动点,沿A→D→C→B→A
的路径匀速移动,设P点经过的路径长为x,
△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
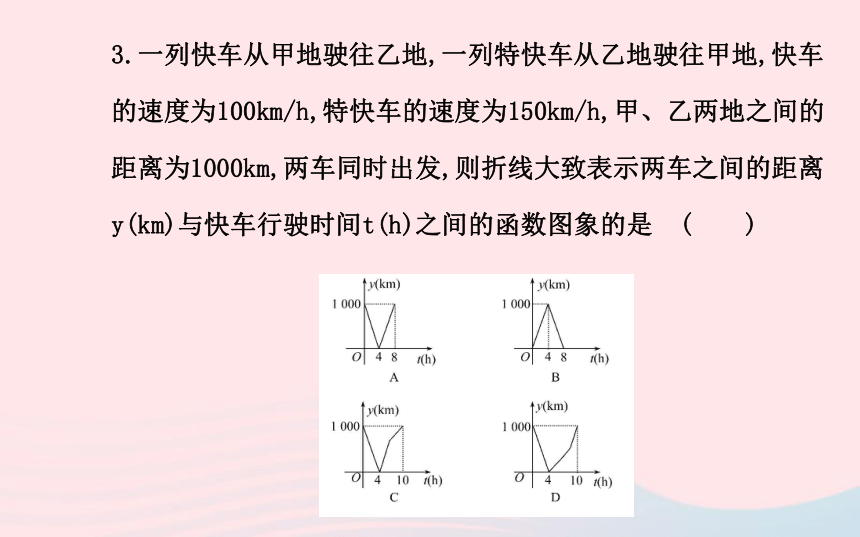
( )【解析】选B.当点P由点A向点D运动时,y的值为0;当点P在DC上运动时,y随着x的增大而增大;当点P在CB上运动时,y不变;当点P在BA上运动时,y随x的增大而减小.3.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100km/h,特快车的速度为150km/h,甲、乙两地之间的距离为1000km,两车同时出发,则折线大致表示两车之间的距离y(km)与快车行驶时间t(h)之间的函数图象的是 ( )【解析】选C.当两车相向出发时,相遇时间t1=1000÷(100+
150)=4(h),且t=4时两车距离y=0,排除B,相遇时,快车已行驶路
程100×4=400(km),还需行驶(1000-400)÷100=6h才能到达乙
地,所以总的时间需要10个小时才能使两车的距离为1000km,故
排除A,而特快车在相遇时已行驶路程为150×4=600(km),只需
行驶(1000-600)÷150= h就可到达甲地,所以当特快车停止行
驶的时候,快车还在行驶,此时总的速度将减慢,即直线的倾斜度
要小些,故选C.考点 2 一次函数的图象与性质?
【知识点睛】
一次函数的图象与性质:【例2】一条直线y=kx+b,其中k+b=-5,kb=6,那么该直线经过 ( )
A.第二、四象限 B.第一、二、三象限
C.第一、三象限 D.第二、三、四象限
【思路点拨】根据k+b=-5,kb=6,分析k,b的符号再确定函数图象经过的象限.
【自主解答】选D.∵kb=6,可知k,b同号,且不为0,
又∵k+b=-5,∴k<0,b<0.
当k<0,b<0时,y=kx+b经过第二、三、四象限.【中考集训】
1.对于函数y=-3x+1,下列结论正确的是 ( )
A.它的图象必经过点(-1,3)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大【解析】选C.将点(-1,3)代入原函数,得y=-3×(-1)+1=4≠3,故A错误;因为k=-3<0,b=1>0,所以图象经过一、二、四象限,y随x的增大而减小,故B,D错误;当x=1时,y=-2<0,故C正确.2.一次函数y=kx+b(k≠0)的
图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0
C.x<2 D.x>2
【解析】选C.由图象可知x=2时,y=0,∵y>0,∴函数图象在x轴的上方,∴x<2.故选C.3.一次函数y=(m+2)x+1,若y随x的增大而增大,则m的取值范围是 .
【解析】由题意得m+2>0,解这个不等式,得m>-2.
答案:m>-2考点 3 用一次函数解决实际问题?
【知识点睛】
日常生活中的许多问题中存在着一次函数关系,用一次函数解决实际问题,就是用运动、变化的观点来分析问题中的数量关系,如方案决策、最优化问题. 应用一次函数解决实际问题的三点注意:
(1)一次函数在现实世界中普遍存在,要注意将实际问题转化成数学问题.
(2)针对一系列相关数据探究函数自变量与对应函数值的关系.
(3)列出函数表达式后,要注意自变量的取值范围.【例3】在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)写出A,B两地之间的距离.
(2)求出点M的坐标,并解释该点坐标所表示的实际意义.
(3)若两人之间的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.【思路点拨】(1)甲的函数图象与y轴交点的纵坐标即是A,B两地间的距离.
(2)利用待定系数法分别求出甲的函数表达式,乙的当x≤1时的函数表达式,联立两个表达式组成方程组,解方程组即可得到点M的坐标.
(3)甲、乙之间的距离不超过3km,即同一时刻甲、乙的函数值之差的绝对值不超过3km,所以列不等式即可求解,要注意的是乙的函数是分段函数.【自主解答】(1)由图可知当x=0时,y=30即当甲出发时离B地距离30 km,∴A,B两地之间的距离是30 km.
(2)设甲的函数表达式为y甲=kx+b(k≠0).
由图象可知 解得
∴甲的表达式为y甲=-15x+30.设乙的表达式为y乙=mx(m≠0,x≤1),代入(1,30)得m=30.
∴乙的表达式为y乙=30x(x≤1).
∴由 解得
∴M点的坐标为 该坐标表示出发 后两人相遇,此时
距离B地20 km.(3)当0≤x≤1时,由(2)可知y甲=-15x+30,y乙=30x.
∴当甲、乙之间的距离不超过3 km时,则|y甲-y乙|≤3.
∴|30-45x|≤3.∴
当1<x≤2时,易知y乙=60-30x.
∴当甲、乙之间的距离不超过3 km时,则|y甲-y乙|≤3,
∴|15x-30|≤3.∴
又∵x≤2,∴
故x的取值范围为【中考集训】
1.周末,小明骑自行车从
家里出发到野外郊游,从家出发1h后到达南
亚所(景点),游玩一段时间后按原速前往湖
光岩.小明离家1h50min后,妈妈驾车沿相同
的路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间.
(2)若妈妈在出发后25min时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数表达式.
【解析】(1)小明骑车的速度为20km/h,在南亚所游玩的时间为1h.(2)设妈妈驾车的速度为x km/h,则
解得x=60(km/h),
点C的坐标为
设直线CD的函数表达式为:y=kx+b(k,b为常数,k≠0),
所以 解得k=60,b=-110,
所以CD所在直线的函数表达式为:y=60x-110.2.某游泳池有水4000m3,现放水清洗池子.同时,工作人员记录放水的时间x(单位:min)与池内水量y(单位:m3)的对应变化的情况,如下表:
(1)根据上表提供的信息,当放水到第80min时,池内有水多少m3?
(2)请你用函数表达式表示y与x的关系,并写出自变量x的取值范围.【解析】(1)4000-25×80=2000(m3),
所以当放水到第80min时,池内有水2000m3.
(2)y=-25x+4000(0≤x≤160).3.A,B两地相距1100m,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2min,乙出发7min后与甲相遇,设甲、乙两人相距ym,甲行进的时间为tmin,y与t之间的函数关系如图所示.请你结合图象探究:(1)甲的行进速度为每分钟 m,m= min.
(2)求直线PQ对应的函数表达式.
(3)求乙的行进速度.【解析】(1)甲的行进速度= =60(m/min),
m=2+7=9(min).
(2)设PQ所在直线的函数表达式为y=kt+b(k,b为常数,k≠0).
∵P(0,1 100),Q(2,980)在直线PQ上,
∴ 解得
∴直线PQ的函数表达式为y=-60t+1 100.
(3)设乙的速度为x m/min.
由题意得60×9+7x=1 100.解得,x=80(m/min),
∴乙的行进速度为80 m/min.4.快、慢两车分别从相距360km路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地.快、慢两车距各自出发地的路程y(km)与出发后所用的时间x(h)的关系如图所示.请结合图象信息解答下列问题:
(1)快、慢两车的速度各是多少?
(2)出发多少小时,快、慢两车距各自出发地的路程相等?
(3)直接写出在慢车到达甲地前,快、慢两车相距的路程为150km的次数.【解析】(1)快车的速度是:
慢车的速度是:360÷(7-1)=60(km/h).
答:快、慢两车的速度分别是120 km/h,60 km/h.
(2)由题意得:OE的函数表达式为:y=60x,BD的函数表达式
为:y=-120x+840.
联立成方程组可解得 ∴出发 快、慢两车距各自
出发地的路程相等.
(3)三次.
第 4 章请写出框图中数字处的内容:
①__________________________________________________
____________________________________________________;
②_______________________;
③____________________________________________;
④___________________;一般地,如果变量y随着变量x而变化,并且对于x取的每一个值,y都有唯一的一个值与它对应,那么我们称y是x的函数图象法、列表法、公式法形如y=kx(k是常数,k≠0)的函数,叫做正比例函数经过原点的一条直线⑤___________________________________________________
________________;
⑥______________________________________________;
⑦_________;
⑧___________________________________________________
________________.当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数一条直线当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小考点 1 分析函数图象解决问题?
【知识点睛】
日常生活中一些不方便使用表达式表示的问题,用图象能简明清晰地反映其意义.分析图象获取信息是中考的热点,这类问题常与生活中的一些热点问题结合,难度不大,多以选择题、填空题为主,其作用在于结合问题的实际背景加深对图象意义的理解.【例1】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州.若该轮船从万州出发后所用的时间为x(h),轮船距万州的距离为y(km),则下列各图形中,能够反映y与x之间函数关系的大致图象是 ( )【思路点拨】将实际问题与函数图象结合起来,分段看图象:
①逆水行驶;②静止不动;③顺水行驶,结合图象判断.
【自主解答】选C.①逆水行驶,y随x的增大而缓慢增大;
②静止不动,y随x的增加不变;
③顺水行驶,y随x的增大快速减小.
结合图象,可得C选项正确.【中考集训】
1.用固定的速度向如图所示形
状的杯子里注水,则能表示杯子里水面的高度和
注水时间的关系的大致图象是 ( )
【解析】选C.容器上粗下细,杯子里水面的高度上升应是先快后慢.2.如图,正方形ABCD的边长
为4,P为正方形边上一动点,沿A→D→C→B→A
的路径匀速移动,设P点经过的路径长为x,
△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
( )【解析】选B.当点P由点A向点D运动时,y的值为0;当点P在DC上运动时,y随着x的增大而增大;当点P在CB上运动时,y不变;当点P在BA上运动时,y随x的增大而减小.3.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100km/h,特快车的速度为150km/h,甲、乙两地之间的距离为1000km,两车同时出发,则折线大致表示两车之间的距离y(km)与快车行驶时间t(h)之间的函数图象的是 ( )【解析】选C.当两车相向出发时,相遇时间t1=1000÷(100+
150)=4(h),且t=4时两车距离y=0,排除B,相遇时,快车已行驶路
程100×4=400(km),还需行驶(1000-400)÷100=6h才能到达乙
地,所以总的时间需要10个小时才能使两车的距离为1000km,故
排除A,而特快车在相遇时已行驶路程为150×4=600(km),只需
行驶(1000-600)÷150= h就可到达甲地,所以当特快车停止行
驶的时候,快车还在行驶,此时总的速度将减慢,即直线的倾斜度
要小些,故选C.考点 2 一次函数的图象与性质?
【知识点睛】
一次函数的图象与性质:【例2】一条直线y=kx+b,其中k+b=-5,kb=6,那么该直线经过 ( )
A.第二、四象限 B.第一、二、三象限
C.第一、三象限 D.第二、三、四象限
【思路点拨】根据k+b=-5,kb=6,分析k,b的符号再确定函数图象经过的象限.
【自主解答】选D.∵kb=6,可知k,b同号,且不为0,
又∵k+b=-5,∴k<0,b<0.
当k<0,b<0时,y=kx+b经过第二、三、四象限.【中考集训】
1.对于函数y=-3x+1,下列结论正确的是 ( )
A.它的图象必经过点(-1,3)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大【解析】选C.将点(-1,3)代入原函数,得y=-3×(-1)+1=4≠3,故A错误;因为k=-3<0,b=1>0,所以图象经过一、二、四象限,y随x的增大而减小,故B,D错误;当x=1时,y=-2<0,故C正确.2.一次函数y=kx+b(k≠0)的
图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0
C.x<2 D.x>2
【解析】选C.由图象可知x=2时,y=0,∵y>0,∴函数图象在x轴的上方,∴x<2.故选C.3.一次函数y=(m+2)x+1,若y随x的增大而增大,则m的取值范围是 .
【解析】由题意得m+2>0,解这个不等式,得m>-2.
答案:m>-2考点 3 用一次函数解决实际问题?
【知识点睛】
日常生活中的许多问题中存在着一次函数关系,用一次函数解决实际问题,就是用运动、变化的观点来分析问题中的数量关系,如方案决策、最优化问题. 应用一次函数解决实际问题的三点注意:
(1)一次函数在现实世界中普遍存在,要注意将实际问题转化成数学问题.
(2)针对一系列相关数据探究函数自变量与对应函数值的关系.
(3)列出函数表达式后,要注意自变量的取值范围.【例3】在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)写出A,B两地之间的距离.
(2)求出点M的坐标,并解释该点坐标所表示的实际意义.
(3)若两人之间的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.【思路点拨】(1)甲的函数图象与y轴交点的纵坐标即是A,B两地间的距离.
(2)利用待定系数法分别求出甲的函数表达式,乙的当x≤1时的函数表达式,联立两个表达式组成方程组,解方程组即可得到点M的坐标.
(3)甲、乙之间的距离不超过3km,即同一时刻甲、乙的函数值之差的绝对值不超过3km,所以列不等式即可求解,要注意的是乙的函数是分段函数.【自主解答】(1)由图可知当x=0时,y=30即当甲出发时离B地距离30 km,∴A,B两地之间的距离是30 km.
(2)设甲的函数表达式为y甲=kx+b(k≠0).
由图象可知 解得
∴甲的表达式为y甲=-15x+30.设乙的表达式为y乙=mx(m≠0,x≤1),代入(1,30)得m=30.
∴乙的表达式为y乙=30x(x≤1).
∴由 解得
∴M点的坐标为 该坐标表示出发 后两人相遇,此时
距离B地20 km.(3)当0≤x≤1时,由(2)可知y甲=-15x+30,y乙=30x.
∴当甲、乙之间的距离不超过3 km时,则|y甲-y乙|≤3.
∴|30-45x|≤3.∴
当1<x≤2时,易知y乙=60-30x.
∴当甲、乙之间的距离不超过3 km时,则|y甲-y乙|≤3,
∴|15x-30|≤3.∴
又∵x≤2,∴
故x的取值范围为【中考集训】
1.周末,小明骑自行车从
家里出发到野外郊游,从家出发1h后到达南
亚所(景点),游玩一段时间后按原速前往湖
光岩.小明离家1h50min后,妈妈驾车沿相同
的路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.(1)求小明骑车的速度和在南亚所游玩的时间.
(2)若妈妈在出发后25min时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数表达式.
【解析】(1)小明骑车的速度为20km/h,在南亚所游玩的时间为1h.(2)设妈妈驾车的速度为x km/h,则
解得x=60(km/h),
点C的坐标为
设直线CD的函数表达式为:y=kx+b(k,b为常数,k≠0),
所以 解得k=60,b=-110,
所以CD所在直线的函数表达式为:y=60x-110.2.某游泳池有水4000m3,现放水清洗池子.同时,工作人员记录放水的时间x(单位:min)与池内水量y(单位:m3)的对应变化的情况,如下表:
(1)根据上表提供的信息,当放水到第80min时,池内有水多少m3?
(2)请你用函数表达式表示y与x的关系,并写出自变量x的取值范围.【解析】(1)4000-25×80=2000(m3),
所以当放水到第80min时,池内有水2000m3.
(2)y=-25x+4000(0≤x≤160).3.A,B两地相距1100m,甲从A地出发,乙从B地出发,相向而行,甲比乙先出发2min,乙出发7min后与甲相遇,设甲、乙两人相距ym,甲行进的时间为tmin,y与t之间的函数关系如图所示.请你结合图象探究:(1)甲的行进速度为每分钟 m,m= min.
(2)求直线PQ对应的函数表达式.
(3)求乙的行进速度.【解析】(1)甲的行进速度= =60(m/min),
m=2+7=9(min).
(2)设PQ所在直线的函数表达式为y=kt+b(k,b为常数,k≠0).
∵P(0,1 100),Q(2,980)在直线PQ上,
∴ 解得
∴直线PQ的函数表达式为y=-60t+1 100.
(3)设乙的速度为x m/min.
由题意得60×9+7x=1 100.解得,x=80(m/min),
∴乙的行进速度为80 m/min.4.快、慢两车分别从相距360km路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地.快、慢两车距各自出发地的路程y(km)与出发后所用的时间x(h)的关系如图所示.请结合图象信息解答下列问题:
(1)快、慢两车的速度各是多少?
(2)出发多少小时,快、慢两车距各自出发地的路程相等?
(3)直接写出在慢车到达甲地前,快、慢两车相距的路程为150km的次数.【解析】(1)快车的速度是:
慢车的速度是:360÷(7-1)=60(km/h).
答:快、慢两车的速度分别是120 km/h,60 km/h.
(2)由题意得:OE的函数表达式为:y=60x,BD的函数表达式
为:y=-120x+840.
联立成方程组可解得 ∴出发 快、慢两车距各自
出发地的路程相等.
(3)三次.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
