2020湘教版八下数学5.2频数直方图习题课件(30张PPT)
文档属性
| 名称 | 2020湘教版八下数学5.2频数直方图习题课件(30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 848.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 08:08:38 | ||
图片预览








文档简介
课件30张PPT。5.2 频数直方图 1.会制作频数直方图.(重点)
2.能用频数直方图解释数据中蕴含的信息.(重点、难点)绘制频数直方图的一般步骤
1.分组:
(1)确定________和________.
(2)确定组距和_____.
把所有数据分成若干组,每个小组的两个端点数据之间的_____
称为组距.最小值m最大值M组数距离2.列____________
统计属于每组中的数据的___________,为避免数据的重复和遗
漏,采用“画记”的方法.
3.绘制频数直方图:
为了更直观地反映一组数据的分布情况,可以以频数分布表为
基础,绘制频数直方图.在直角坐标系中,以_____为宽,_____为
高作小矩形即可.频数分布表:个数(频数)组距频数【归纳】绘制频数直方图应注意的问题
(1)在横轴和纵轴上加上适当的刻度,标明各轴代表的_____和
_____.
(2)各个小矩形之间_______.
(3)小矩形的边界对应于_____的组界.名称单位无空隙各组 (打“√”或“×”)
(1)直方图就是条形图.( )
(2)画直方图等距分组时,可以用小长方形的高表示频数.( )
(3)一组数据分组时,组距和组数都不是唯一的.( )
(4)一组数据的最大值与最小值的差是23,若组距是4,则
=5.75,所以该组数据应分5组.( )
(5)各组的组距可以相同也可以彼此不同.( )×√√×√知识点 用频数直方图解决问题?
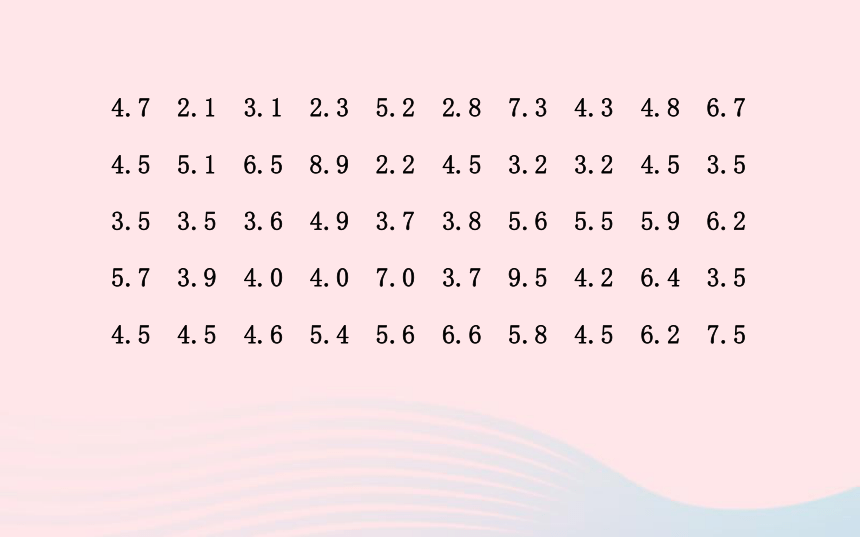
【例】某区在实施居民用水定额管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:t),并将调查数据进行了整理:4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
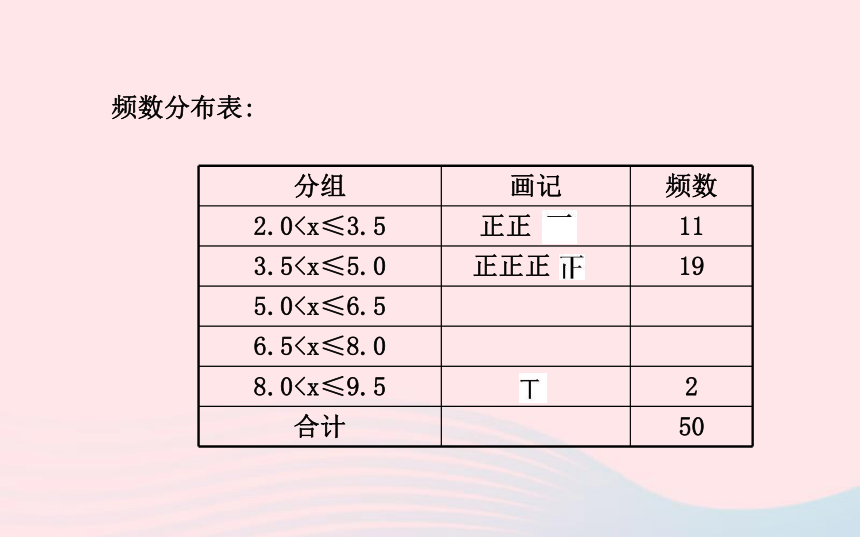
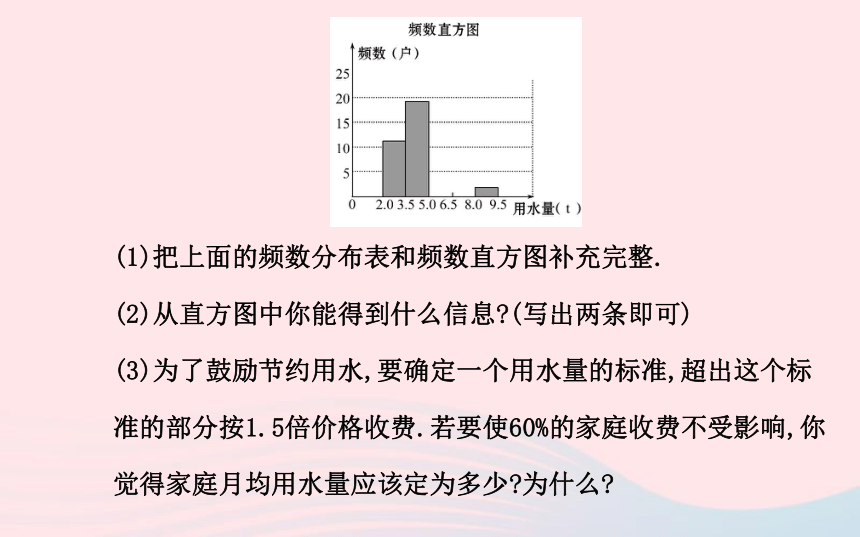
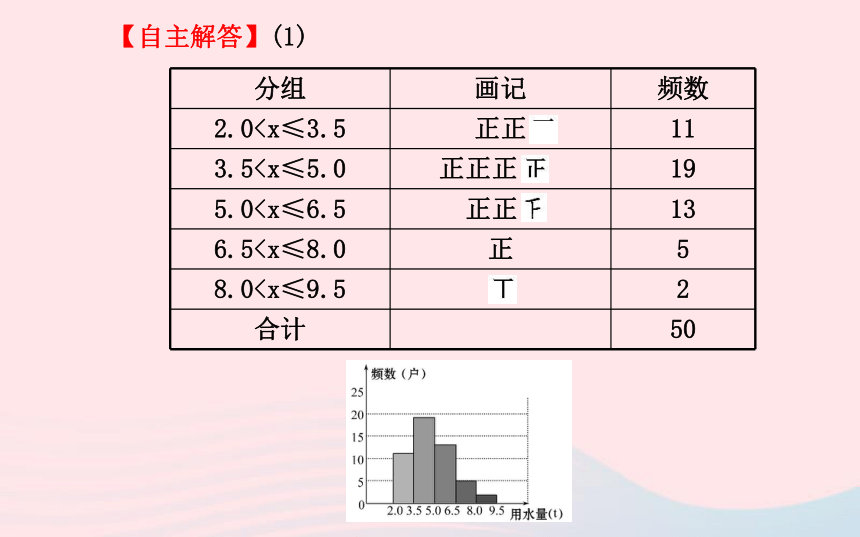
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5频数分布表:(1)把上面的频数分布表和频数直方图补充完整.
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?【思路点拨】(1)用画记的方法统计频数分布表中未知的两个范围的频数,从而补表、补图.
(2)答案不唯一:如用水最多或最少的范围,多数人用水的范围等.
(3)由低到高统计30户家庭用水在什么范围.【自主解答】(1)(2)答案不唯一:如①从直方图可以看出:居民月均用水量大
部分在2.0至6.5之间;②居民月均用水量在3.5最多,有19户;③居民月均用水量在8.0少,只有2户等.(合理即可)
(3)要使60%的家庭收费不受影响,家庭月均用水量应该定为
5 t,因为月均用水量不超过5 t的有30户, ×100%=60%.【总结提升】频数直方图与条形统计图的异同
1.相同点:都易于比较各数据间的差别;都可以直观地表示出具体数量.
2.不同点:(1)频数直方图表示的是连续分组数据,直方图中的各矩形通常是连续排列的,而条形统计图表示的是离散数据,各矩形通常是分开排列的.
(2)频数直方图是表示同一类事物中一组数据的分布情况,而条形统计图可以表示不同类事物之间的分布情况.题组:用频数直方图解决问题
1.依据某校九年级一班在体育毕业考试中全班所有学生成绩,制成的频数直方图如图(学生成绩取整数),则成绩在21.5~24.5这一分数段的频数和频率分别是 ( )【解析】选C.观察频数直方图可知:共1+4+10+15+20=50(名)
学生,读图可知成绩在21.5~24.5这一分数段的频数是10,故
其频率是 =0.2.A.4,0.1 B.10,0.1 C.10,0.2 D.20,0.22.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频数直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组的频数是12,则此次抽样的样本容量是 .【解析】根据频数直方图中每一组内的频率总和等于1,可知第六组的频率为1-0.94=0.06,因为第六组的频数是12,所以此次抽样的样本容量是12÷0.06=200.
答案:2003.某区对参加2019年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数直方图的一部分.请根据图表信息回答下列问题:(1)在频数分布表中,a的值为 ,b的值为 ,并将频数直方图补充完整.
(2)甲同学说:“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围.
(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 ;并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?【解析】(1)∵20÷0.1=200,
∴a=200-20-40-70-10=60,b=10÷200=0.05;
补全直方图如图所示.(2)∵根据中位数的定义知道中位数在4.6≤x<4.9,∴甲同学
的视力情况范围:4.6≤x<4.9.
(3)视力正常的人数占被统计人数的百分比是:
=35%,
∴估计全区初中毕业生中视力正常的学生有35%×5 000=
1 750(人). 4.在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动开展的情况,随机调查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成两个不完整的统计图.请根据图中提供的信息,解答下列问题:(1)本次共抽查了多少名学生?
(2)请补全频数直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形圆心角的度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.【解析】(1)(16+8)÷12%=200(名).
答:本次共抽查了200名学生.
(2)范围是135≤x<145的人数是200-8-16-71-60-16=29(人),
补全频数直方图如图所示:
则跳绳次数范围135≤x<155所在扇形的圆心角度数是(3) =4 200(名).
(4)(观点积极健康向上即可)如全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.5.为了进一步了解某校九年级学生的身体素质,体育老师从该年级各班中随机抽取50名学生进行1分钟跳绳次数测试,以测试数据为样本,绘制出图表.(1)求表中a和b的值:a= ;b= .
(2)请将频数直方图补充完整.
(3)若在1分钟内跳绳次数大于等于120次认定为合格,则从全年级任意抽测一位同学为合格的概率是多少?
(4)今年该校九年级有320名学生,请你估算九年级跳绳项目不合格的学生约有多少人?【解析】(1)50-4-6-18-10=12,
∴a=12, =0.24,∴b=0.24.
(2)120~140,18人;140~160,12人,频数直方图如图:
(3)P(合格)=1-0.08-0.12=0.80.
(4)320×(0.08+0.12)=64(人).【想一想错在哪?】如图是某班一次数学测试成绩的频数直方图,根据图中的信息可知成绩最高两组的人数和有 人.
提示:小长方形的高表示人数而不表示成绩.
2.能用频数直方图解释数据中蕴含的信息.(重点、难点)绘制频数直方图的一般步骤
1.分组:
(1)确定________和________.
(2)确定组距和_____.
把所有数据分成若干组,每个小组的两个端点数据之间的_____
称为组距.最小值m最大值M组数距离2.列____________
统计属于每组中的数据的___________,为避免数据的重复和遗
漏,采用“画记”的方法.
3.绘制频数直方图:
为了更直观地反映一组数据的分布情况,可以以频数分布表为
基础,绘制频数直方图.在直角坐标系中,以_____为宽,_____为
高作小矩形即可.频数分布表:个数(频数)组距频数【归纳】绘制频数直方图应注意的问题
(1)在横轴和纵轴上加上适当的刻度,标明各轴代表的_____和
_____.
(2)各个小矩形之间_______.
(3)小矩形的边界对应于_____的组界.名称单位无空隙各组 (打“√”或“×”)
(1)直方图就是条形图.( )
(2)画直方图等距分组时,可以用小长方形的高表示频数.( )
(3)一组数据分组时,组距和组数都不是唯一的.( )
(4)一组数据的最大值与最小值的差是23,若组距是4,则
=5.75,所以该组数据应分5组.( )
(5)各组的组距可以相同也可以彼此不同.( )×√√×√知识点 用频数直方图解决问题?
【例】某区在实施居民用水定额管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:t),并将调查数据进行了整理:4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5频数分布表:(1)把上面的频数分布表和频数直方图补充完整.
(2)从直方图中你能得到什么信息?(写出两条即可)
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费.若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?【思路点拨】(1)用画记的方法统计频数分布表中未知的两个范围的频数,从而补表、补图.
(2)答案不唯一:如用水最多或最少的范围,多数人用水的范围等.
(3)由低到高统计30户家庭用水在什么范围.【自主解答】(1)(2)答案不唯一:如①从直方图可以看出:居民月均用水量大
部分在2.0至6.5之间;②居民月均用水量在3.5
(3)要使60%的家庭收费不受影响,家庭月均用水量应该定为
5 t,因为月均用水量不超过5 t的有30户, ×100%=60%.【总结提升】频数直方图与条形统计图的异同
1.相同点:都易于比较各数据间的差别;都可以直观地表示出具体数量.
2.不同点:(1)频数直方图表示的是连续分组数据,直方图中的各矩形通常是连续排列的,而条形统计图表示的是离散数据,各矩形通常是分开排列的.
(2)频数直方图是表示同一类事物中一组数据的分布情况,而条形统计图可以表示不同类事物之间的分布情况.题组:用频数直方图解决问题
1.依据某校九年级一班在体育毕业考试中全班所有学生成绩,制成的频数直方图如图(学生成绩取整数),则成绩在21.5~24.5这一分数段的频数和频率分别是 ( )【解析】选C.观察频数直方图可知:共1+4+10+15+20=50(名)
学生,读图可知成绩在21.5~24.5这一分数段的频数是10,故
其频率是 =0.2.A.4,0.1 B.10,0.1 C.10,0.2 D.20,0.22.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频数直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组的频数是12,则此次抽样的样本容量是 .【解析】根据频数直方图中每一组内的频率总和等于1,可知第六组的频率为1-0.94=0.06,因为第六组的频数是12,所以此次抽样的样本容量是12÷0.06=200.
答案:2003.某区对参加2019年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数直方图的一部分.请根据图表信息回答下列问题:(1)在频数分布表中,a的值为 ,b的值为 ,并将频数直方图补充完整.
(2)甲同学说:“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围.
(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 ;并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?【解析】(1)∵20÷0.1=200,
∴a=200-20-40-70-10=60,b=10÷200=0.05;
补全直方图如图所示.(2)∵根据中位数的定义知道中位数在4.6≤x<4.9,∴甲同学
的视力情况范围:4.6≤x<4.9.
(3)视力正常的人数占被统计人数的百分比是:
=35%,
∴估计全区初中毕业生中视力正常的学生有35%×5 000=
1 750(人). 4.在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动开展的情况,随机调查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成两个不完整的统计图.请根据图中提供的信息,解答下列问题:(1)本次共抽查了多少名学生?
(2)请补全频数直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形圆心角的度数.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.【解析】(1)(16+8)÷12%=200(名).
答:本次共抽查了200名学生.
(2)范围是135≤x<145的人数是200-8-16-71-60-16=29(人),
补全频数直方图如图所示:
则跳绳次数范围135≤x<155所在扇形的圆心角度数是(3) =4 200(名).
(4)(观点积极健康向上即可)如全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.5.为了进一步了解某校九年级学生的身体素质,体育老师从该年级各班中随机抽取50名学生进行1分钟跳绳次数测试,以测试数据为样本,绘制出图表.(1)求表中a和b的值:a= ;b= .
(2)请将频数直方图补充完整.
(3)若在1分钟内跳绳次数大于等于120次认定为合格,则从全年级任意抽测一位同学为合格的概率是多少?
(4)今年该校九年级有320名学生,请你估算九年级跳绳项目不合格的学生约有多少人?【解析】(1)50-4-6-18-10=12,
∴a=12, =0.24,∴b=0.24.
(2)120~140,18人;140~160,12人,频数直方图如图:
(3)P(合格)=1-0.08-0.12=0.80.
(4)320×(0.08+0.12)=64(人).【想一想错在哪?】如图是某班一次数学测试成绩的频数直方图,根据图中的信息可知成绩最高两组的人数和有 人.
提示:小长方形的高表示人数而不表示成绩.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
