四年级数学下册 《探索与发现:三角形内角和》同步练习3-北师大版(含答案)
文档属性
| 名称 | 四年级数学下册 《探索与发现:三角形内角和》同步练习3-北师大版(含答案) | 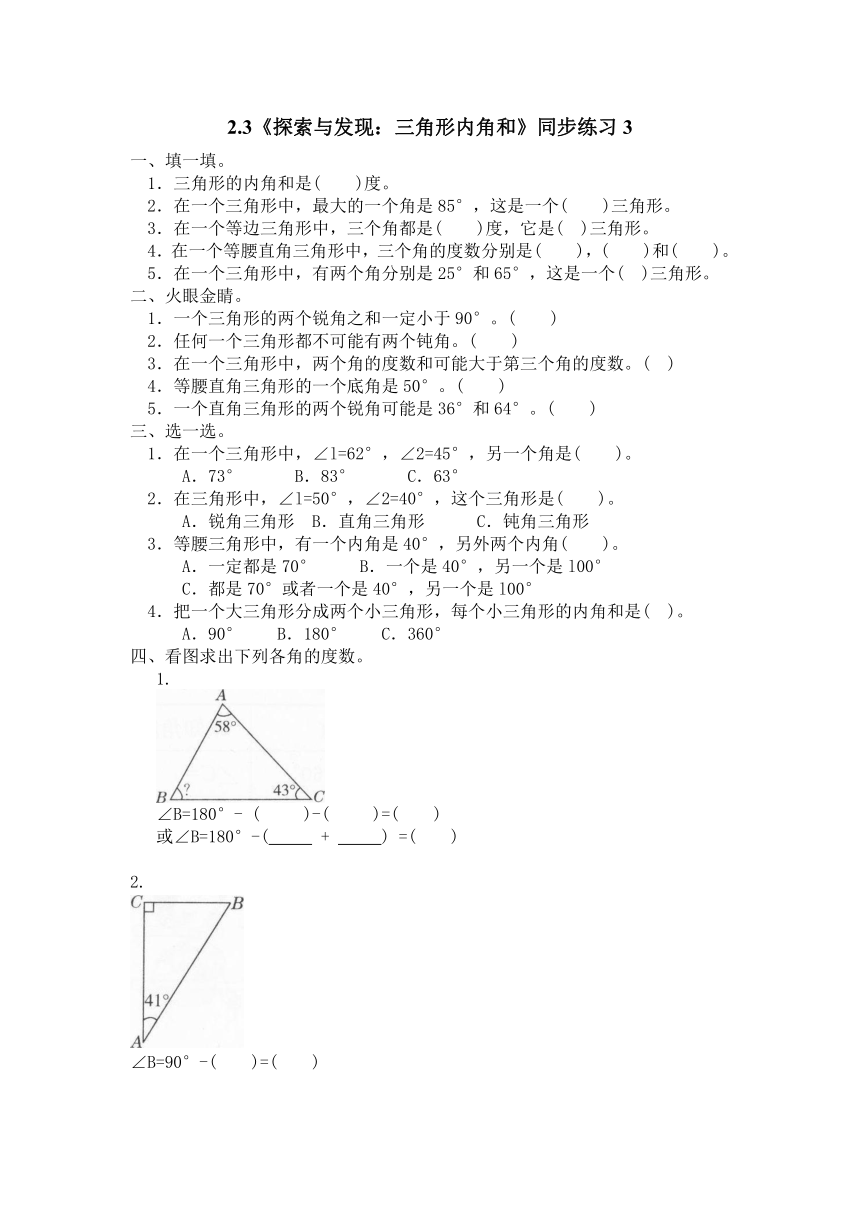 | |
| 格式 | zip | ||
| 文件大小 | 54.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-13 22:55:36 | ||
图片预览

文档简介
2.3《探索与发现:三角形内角和》同步练习3
一、填一填。
1.三角形的内角和是( )度。
2.在一个三角形中,最大的一个角是85°,这是一个( )三角形。
3.在一个等边三角形中,三个角都是( )度,它是( )三角形。
4.在一个等腰直角三角形中,三个角的度数分别是( ),( )和( )。
5.在一个三角形中,有两个角分别是25°和65°,这是一个( )三角形。
二、火眼金睛。
1.一个三角形的两个锐角之和一定小于90°。( )
2.任何一个三角形都不可能有两个钝角。( )
3.在一个三角形中,两个角的度数和可能大于第三个角的度数。( )
4.等腰直角三角形的一个底角是50°。( )
5.一个直角三角形的两个锐角可能是36°和64°。( )
三、选一选。
1.在一个三角形中,∠l=62°,∠2=45°,另一个角是( )。
A.73° B.83° C.63°
2.在三角形中,∠l=50°,∠2=40°,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形
3.等腰三角形中,有一个内角是40°,另外两个内角( )。
A.一定都是70° B.一个是40°,另一个是l00°
C.都是70°或者一个是40°,另一个是l00°
4.把一个大三角形分成两个小三角形,每个小三角形的内角和是( )。
A.90° B.180° C.360°
四、看图求出下列各角的度数。
1.
∠B=180°- ( )-( )=( )
或∠B=180°-( + ) =( )
2.
∠B=90°-( )=( )
3.
∠C=180°-( )-( )=( )
五、根据所给条件求出各角的度数。
在等腰三角形ABC中,∠1是底角,∠2是顶角。
如果∠l=30°,求∠2。
如果∠2是直角,求∠l。
六、如图,∠l=125°,∠3=45°,求∠4=?
七、已知三角形ABC是等腰三角形,∠A=80°,∠1=∠2,∠3=∠4,求∠5的度数。
参考答案
一、
1.180
2.锐角
3.60 锐角
4.90° 45° 45°
5.直角
二、1.× 2.√ 3.√ 4.× 5.×
三、1.A 2.B 3.C 4.B
四、
1.∠B=180°-58°-43°=79°或∠B=180°-(58°+43°)=79°
2.∠B=90°-41°=49°
3.∠C=180°-30°-38°=112°
五、1. ∠2=120° 2. ∠1=45°
六、∠2=180°-125°=55° ∠4=180°-55°-45°=80°
七、(180°-80°)÷2=50°
∠2=50°÷2=25°
∠4=50°÷2=25°
∠5=180°-25°-25°=130°
一、填一填。
1.三角形的内角和是( )度。
2.在一个三角形中,最大的一个角是85°,这是一个( )三角形。
3.在一个等边三角形中,三个角都是( )度,它是( )三角形。
4.在一个等腰直角三角形中,三个角的度数分别是( ),( )和( )。
5.在一个三角形中,有两个角分别是25°和65°,这是一个( )三角形。
二、火眼金睛。
1.一个三角形的两个锐角之和一定小于90°。( )
2.任何一个三角形都不可能有两个钝角。( )
3.在一个三角形中,两个角的度数和可能大于第三个角的度数。( )
4.等腰直角三角形的一个底角是50°。( )
5.一个直角三角形的两个锐角可能是36°和64°。( )
三、选一选。
1.在一个三角形中,∠l=62°,∠2=45°,另一个角是( )。
A.73° B.83° C.63°
2.在三角形中,∠l=50°,∠2=40°,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形
3.等腰三角形中,有一个内角是40°,另外两个内角( )。
A.一定都是70° B.一个是40°,另一个是l00°
C.都是70°或者一个是40°,另一个是l00°
4.把一个大三角形分成两个小三角形,每个小三角形的内角和是( )。
A.90° B.180° C.360°
四、看图求出下列各角的度数。
1.
∠B=180°- ( )-( )=( )
或∠B=180°-( + ) =( )
2.
∠B=90°-( )=( )
3.
∠C=180°-( )-( )=( )
五、根据所给条件求出各角的度数。
在等腰三角形ABC中,∠1是底角,∠2是顶角。
如果∠l=30°,求∠2。
如果∠2是直角,求∠l。
六、如图,∠l=125°,∠3=45°,求∠4=?
七、已知三角形ABC是等腰三角形,∠A=80°,∠1=∠2,∠3=∠4,求∠5的度数。
参考答案
一、
1.180
2.锐角
3.60 锐角
4.90° 45° 45°
5.直角
二、1.× 2.√ 3.√ 4.× 5.×
三、1.A 2.B 3.C 4.B
四、
1.∠B=180°-58°-43°=79°或∠B=180°-(58°+43°)=79°
2.∠B=90°-41°=49°
3.∠C=180°-30°-38°=112°
五、1. ∠2=120° 2. ∠1=45°
六、∠2=180°-125°=55° ∠4=180°-55°-45°=80°
七、(180°-80°)÷2=50°
∠2=50°÷2=25°
∠4=50°÷2=25°
∠5=180°-25°-25°=130°
