人教版八年级下册数学 18.2.2菱形课件(2课时共37张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.2.2菱形课件(2课时共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 07:33:22 | ||
图片预览


文档简介
(共37张PPT)
18.2.2
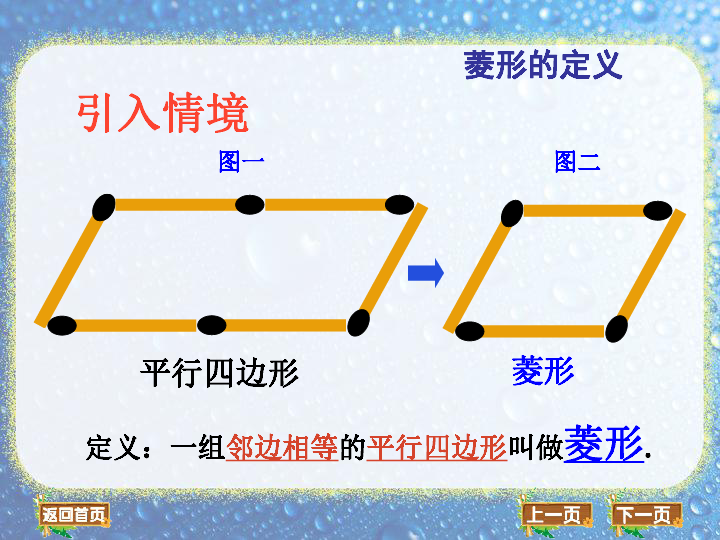
引入情境
菱形的定义
图一
图二
平行四边形
菱形
定义:一组邻边相等的平行四边形叫做菱形.
联系生活
生活中常见的菱形
实践探究
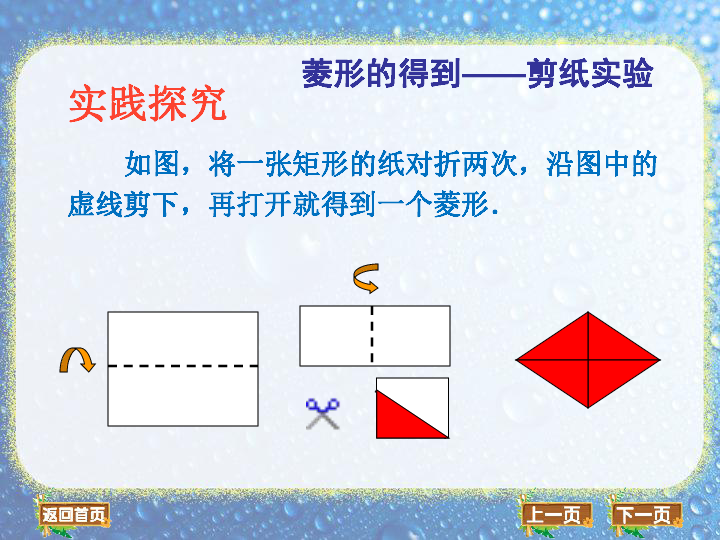
菱形的得到——剪纸实验
如图,将一张矩形的纸对折两次,沿图中的虚线剪下,再打开就得到一个菱形.
探索发现
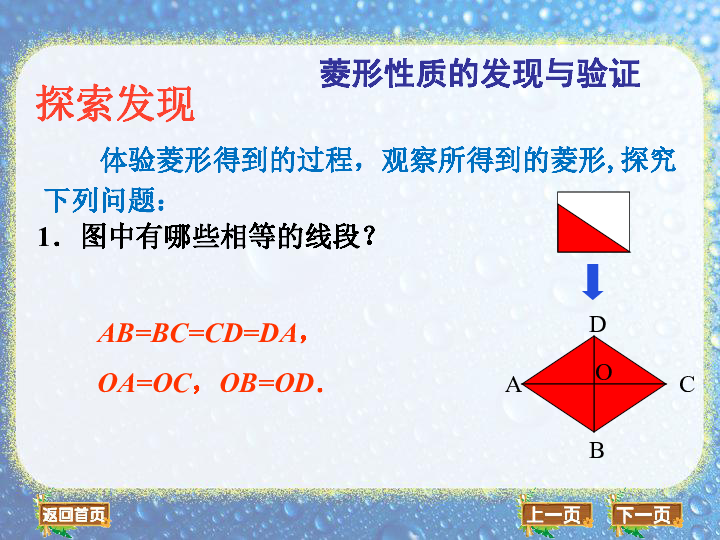
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
1.图中有哪些相等的线段?
A
D
C
B
O
AB=BC=CD=DA,
OA=OC,OB=OD.
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
2 .图中有哪些相等的角?
A
D
C
B
O
∠ACD=∠ACB=∠CAD=∠CAB,∠ABD=∠CBD=∠ADB=∠CDB,
∠ADC=∠ABC,∠BAD=∠BCD,
∠AOD=∠AOB=∠COB=∠COD=90°.
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
3.图中有哪些等腰三角形,会全等吗?
A
D
C
B
O
等腰△ABD≌等腰△CBD,
等腰△DAC≌等腰△BAC ;
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
4.图中有哪些直角三角形,会全等吗?
A
D
C
B
O
Rt△AOB≌Rt△COB≌Rt△DOC≌Rt△AOD.
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
5.菱形是轴对称图形吗?
它有几条对称轴,分别是什么?
对称轴之间有什么位置关系?
A
D
C
B
O
菱形是轴对称图形,有2条对称轴,
分别是菱形的两条对角线,
两条对称轴互相垂直.
探索发现
规律总结
菱形性质的归纳
A
D
C
B
O
1.菱形的四条边相等;
2.菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
菱形是特殊的平行四边形,具有平行四边形的所有性质.并还具有以下特殊性质:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
∵四边形ABCD是菱形,
∴ AC⊥BD ,∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB= ∠CDB,∠ABD=∠CBD.
菱形的两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
A
D
C
B
O
菱形的性质
【菱形的面积公式】
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
规律应用
菱形性质的应用
1.如图,菱形ABCD的对角线AC,BD相交于点O.
A
B
C
D
O
①若已知AC=12cm,BD=16cm,
则AO=_______cm;
BO=_______cm;
AB=_______cm;
菱形ABCD的周长是_______cm。
6
8
10
40
菱形性质的应用
A
B
C
D
O
30°
60°
6
②若已知∠BAD=120°,AB=6cm,
则∠ACB=______;
∠CBO=______;
AC=_______cm;
BD=_______cm.
规律应用
如图,菱形ABCD的对角线AC,BD相交于点O.
菱形性质的应用
A
B
C
D
O
③若已知AO=3cm,BO=4cm,则
菱形ABCD的面积是=_______cm2.
24
如图,菱形ABCD的对角线AC,BD相交于点O.
实战演练
菱形性质的应用
2.如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积
实战演练
菱形性质的应用
3.如图,已知两个菱形ABCD,CEFG,其中点
A,C,F在同一直线上,连接BE,DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.
解(1) :△ADC≌△ABC,△GFC≌△EFC;
证明(2) :∵四边形ABCD,CEFG是菱形,
∴DC=BC,CG=CE,
∠DCA=∠BCA,∠GCF=∠ECF.
∵∠ACF=180°,
∴∠DCG=∠BCE.
则在△DCG和△BCE中有DC=BC,∠DCG=∠BCE,CG=CE,
∴△DCG≌△BCE,
∴BE=DG.
4
小结反思
本课小结
平行四边形
菱形
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形的四条边相等;
菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
2.性质:
3.菱形的面积= 底×高=两对角线乘积的一半.
第2课时 菱形的判定
菱形
类比引入
复习与回顾
1.你知道矩形的判定有哪些方法吗?
2. 你知道菱形的定义吗?
3.想一想,菱形的判定会有哪些方法呢
①有一角是直角的平行四边形是矩形
②对角线相等的平行四边形是矩形
③三个角都是直角的四边形是矩形
你知道菱形的特殊的性质吗?
矩形的定义
矩形的对角线相等
矩形的四个角都是直角
有一组邻边相等的平行四边形叫做菱形
菱形的四条边都相等
菱形的两条对角线互相垂直
联想验证
菱形的判定1
有一组邻边相等的平行四边形是菱形.
判定方法一(定义法) :
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
∵ 在□ABCD中, AB=BC,
∴ □ABCD是菱形.
菱形的判定2
判定方法二:
对角线互相垂直的平行四边形是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
AC⊥BD
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
你能证明吗?
联想验证
菱形的判定2
命题
已知:在□ABCD 中,对角线AC,BD交于点O,
且AC ⊥ BD于点O.
求证: □ABCD 是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD于点O,
∴BA=BC.
∴ □ABCD是菱形.
∴BD是AC的垂直平分线 .
对角线互相垂直的平行四边形是菱形.
定理
联想验证
菱形的判定3
判定方法三:
四边相等的四边形是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
∴ □ABCD是菱形.
AB=BC=CD=DA
∵在四边形ABCD中, AB=BC=CD=DA,
你能证明吗?
联想验证
菱形的判定3
命题
已知:在四边形ABCD 中,AB=BC=CD=DA.
求证: □ABCD 是菱形.
证明:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴ □ABCD是菱形.
四边相等的四边形是菱形.
定理
D
A
B
C
联想验证
小结归纳
菱形的判定方法小结
菱形的判定方法:
①有一组邻边相等的平行四边形是菱形
②对角线互相垂直的平行四边形是菱形
③四边相等的四边形是菱形
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形何时候变成菱形?
体验
一
当两根木条互相垂直时,这个四边形变成菱形.
小结归纳
菱形的判定方法小结
菱形的判定方法:
①有一组邻边相等的平行四边形是菱形
②对角线互相垂直的平行四边形是菱形
③四边相等的四边形是菱形
体验
二
先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB为半径画弧,得到两弧的交点C,连接BC,DC.
你能用尺规作图画菱形吗?
A
B
D
C
所得四边形ABCD
即为菱形 .
尝试应用
菱形的判定例题
例1:如图,□ABCD 的对角线AC,BD交于点O,
且AB=5,AO=4,BO=3.求证: □ABCD是菱形.
A
B
C
D
O
5
4
3
证明:∵AB=5,AO=4,BO=3,
∴
∴△OAB是直角三角形,
即AC⊥BD
∴□ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
尝试应用
菱形的判定例题
例2:如图,矩形ABCD的对角线AC,BD相交于
点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
A
B
C
D
O
E
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OC= AC,OD= BD.
∴OC=OD,
∴四边形OCED是菱形.(有一组邻边相等的平行四边形是菱形)
证明:∵AE是∠BAD的平分线,
∴∠BAE=∠DAE.
又AB=AD,AE=AE,
∴△ABE≌△ADE(SAS).
∴BE=DE.
∵AD∥BC,
∴∠DAE=∠AEB.∴∠BAE=∠AEB.
∴AB=BE.
∴AD=AB=BE=DE.
∴四边形ABED是菱形.(四边相等的四边形是菱形)
尝试应用
菱形的判定例题
例3:如图,在四边形ABCD中,AD∥BC, AB=AD,∠BAD的平分线AE交BC于点E,连接DE.求证:四边形ABED是菱形.
D
A
B
C
E
1
2
3
尝试应用
菱形的判定例题
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
独立思考
可以用哪个判定方法呢?
尝试应用
菱形的判定例题
方法1:
证明:∵EF是AC的垂直平分线,
∴EA=EC,FA=FC,
AO=CO,∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO
∴△AOE≌△COF(ASA).
∴EA=FC.
∴EC=EA=FC=FA.
∴四边形AFCE是菱形.(四边相等的四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
尝试应用
菱形的判定例题
方法2:
证明:∵EF是AC的垂直平分线,
∴EA=EC,AO=CO,
∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∴△AOE≌△COF(ASA).
∴OE=OF.∴四边形AFCE是平行四边形.
又∵EA=EC,∴□AFCE是菱形.(有一组邻边相等的平行四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
尝试应用
菱形的判定例题
方法3:
证明:∵EF是AC的垂直平分线,
∴AC⊥EF,AO=CO,
∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∴△AOE≌△COF(ASA).
∴OE=OF.∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴□AFCE是菱形.(对角线互相垂直的平行四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
小结反思
本课小结
1.如何判定一个四边形为菱形?
2.解决判定菱形的问题最关键的是什么?
3.谈一谈你的收获与体会?
18.2.2
引入情境
菱形的定义
图一
图二
平行四边形
菱形
定义:一组邻边相等的平行四边形叫做菱形.
联系生活
生活中常见的菱形
实践探究
菱形的得到——剪纸实验
如图,将一张矩形的纸对折两次,沿图中的虚线剪下,再打开就得到一个菱形.
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
1.图中有哪些相等的线段?
A
D
C
B
O
AB=BC=CD=DA,
OA=OC,OB=OD.
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
2 .图中有哪些相等的角?
A
D
C
B
O
∠ACD=∠ACB=∠CAD=∠CAB,∠ABD=∠CBD=∠ADB=∠CDB,
∠ADC=∠ABC,∠BAD=∠BCD,
∠AOD=∠AOB=∠COB=∠COD=90°.
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
3.图中有哪些等腰三角形,会全等吗?
A
D
C
B
O
等腰△ABD≌等腰△CBD,
等腰△DAC≌等腰△BAC ;
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
4.图中有哪些直角三角形,会全等吗?
A
D
C
B
O
Rt△AOB≌Rt△COB≌Rt△DOC≌Rt△AOD.
探索发现
菱形性质的发现与验证
体验菱形得到的过程,观察所得到的菱形,探究下列问题:
5.菱形是轴对称图形吗?
它有几条对称轴,分别是什么?
对称轴之间有什么位置关系?
A
D
C
B
O
菱形是轴对称图形,有2条对称轴,
分别是菱形的两条对角线,
两条对称轴互相垂直.
探索发现
规律总结
菱形性质的归纳
A
D
C
B
O
1.菱形的四条边相等;
2.菱形的对角线互相垂直,
并且每一条对角线平分一组对角.
菱形是特殊的平行四边形,具有平行四边形的所有性质.并还具有以下特殊性质:
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.
∵四边形ABCD是菱形,
∴ AC⊥BD ,∠DAC=∠BAC,∠DCA=∠BCA,
∠ADB= ∠CDB,∠ABD=∠CBD.
菱形的两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,每一条对角线平分一组对角.
A
D
C
B
O
菱形的性质
【菱形的面积公式】
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗?
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
规律应用
菱形性质的应用
1.如图,菱形ABCD的对角线AC,BD相交于点O.
A
B
C
D
O
①若已知AC=12cm,BD=16cm,
则AO=_______cm;
BO=_______cm;
AB=_______cm;
菱形ABCD的周长是_______cm。
6
8
10
40
菱形性质的应用
A
B
C
D
O
30°
60°
6
②若已知∠BAD=120°,AB=6cm,
则∠ACB=______;
∠CBO=______;
AC=_______cm;
BD=_______cm.
规律应用
如图,菱形ABCD的对角线AC,BD相交于点O.
菱形性质的应用
A
B
C
D
O
③若已知AO=3cm,BO=4cm,则
菱形ABCD的面积是=_______cm2.
24
如图,菱形ABCD的对角线AC,BD相交于点O.
实战演练
菱形性质的应用
2.如图,菱形花坛ABCD的边长为20m, ∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积
实战演练
菱形性质的应用
3.如图,已知两个菱形ABCD,CEFG,其中点
A,C,F在同一直线上,连接BE,DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.
解(1) :△ADC≌△ABC,△GFC≌△EFC;
证明(2) :∵四边形ABCD,CEFG是菱形,
∴DC=BC,CG=CE,
∠DCA=∠BCA,∠GCF=∠ECF.
∵∠ACF=180°,
∴∠DCG=∠BCE.
则在△DCG和△BCE中有DC=BC,∠DCG=∠BCE,CG=CE,
∴△DCG≌△BCE,
∴BE=DG.
4
小结反思
本课小结
平行四边形
菱形
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形的四条边相等;
菱形的两条对角线互相垂直,并且每一条对
角线平分一组对角.
2.性质:
3.菱形的面积= 底×高=两对角线乘积的一半.
第2课时 菱形的判定
菱形
类比引入
复习与回顾
1.你知道矩形的判定有哪些方法吗?
2. 你知道菱形的定义吗?
3.想一想,菱形的判定会有哪些方法呢
①有一角是直角的平行四边形是矩形
②对角线相等的平行四边形是矩形
③三个角都是直角的四边形是矩形
你知道菱形的特殊的性质吗?
矩形的定义
矩形的对角线相等
矩形的四个角都是直角
有一组邻边相等的平行四边形叫做菱形
菱形的四条边都相等
菱形的两条对角线互相垂直
联想验证
菱形的判定1
有一组邻边相等的平行四边形是菱形.
判定方法一(定义法) :
AB=BC
A
B
C
D
□ABCD
A
B
C
D
菱形ABCD
∵ 在□ABCD中, AB=BC,
∴ □ABCD是菱形.
菱形的判定2
判定方法二:
对角线互相垂直的平行四边形是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
AC⊥BD
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
你能证明吗?
联想验证
菱形的判定2
命题
已知:在□ABCD 中,对角线AC,BD交于点O,
且AC ⊥ BD于点O.
求证: □ABCD 是菱形.
A
B
C
D
O
∟
证明:
∵四边形ABCD是平行四边形,
∴OA=OC.
又∵AC⊥BD于点O,
∴BA=BC.
∴ □ABCD是菱形.
∴BD是AC的垂直平分线 .
对角线互相垂直的平行四边形是菱形.
定理
联想验证
菱形的判定3
判定方法三:
四边相等的四边形是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
∴ □ABCD是菱形.
AB=BC=CD=DA
∵在四边形ABCD中, AB=BC=CD=DA,
你能证明吗?
联想验证
菱形的判定3
命题
已知:在四边形ABCD 中,AB=BC=CD=DA.
求证: □ABCD 是菱形.
证明:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
又∵AB=AD,
∴ □ABCD是菱形.
四边相等的四边形是菱形.
定理
D
A
B
C
联想验证
小结归纳
菱形的判定方法小结
菱形的判定方法:
①有一组邻边相等的平行四边形是菱形
②对角线互相垂直的平行四边形是菱形
③四边相等的四边形是菱形
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形何时候变成菱形?
体验
一
当两根木条互相垂直时,这个四边形变成菱形.
小结归纳
菱形的判定方法小结
菱形的判定方法:
①有一组邻边相等的平行四边形是菱形
②对角线互相垂直的平行四边形是菱形
③四边相等的四边形是菱形
体验
二
先画两条等长的线段AB,AD,然后分别以B,D为圆心,AB为半径画弧,得到两弧的交点C,连接BC,DC.
你能用尺规作图画菱形吗?
A
B
D
C
所得四边形ABCD
即为菱形 .
尝试应用
菱形的判定例题
例1:如图,□ABCD 的对角线AC,BD交于点O,
且AB=5,AO=4,BO=3.求证: □ABCD是菱形.
A
B
C
D
O
5
4
3
证明:∵AB=5,AO=4,BO=3,
∴
∴△OAB是直角三角形,
即AC⊥BD
∴□ABCD是菱形.
(对角线互相垂直的平行四边形是菱形)
尝试应用
菱形的判定例题
例2:如图,矩形ABCD的对角线AC,BD相交于
点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
A
B
C
D
O
E
证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OC= AC,OD= BD.
∴OC=OD,
∴四边形OCED是菱形.(有一组邻边相等的平行四边形是菱形)
证明:∵AE是∠BAD的平分线,
∴∠BAE=∠DAE.
又AB=AD,AE=AE,
∴△ABE≌△ADE(SAS).
∴BE=DE.
∵AD∥BC,
∴∠DAE=∠AEB.∴∠BAE=∠AEB.
∴AB=BE.
∴AD=AB=BE=DE.
∴四边形ABED是菱形.(四边相等的四边形是菱形)
尝试应用
菱形的判定例题
例3:如图,在四边形ABCD中,AD∥BC, AB=AD,∠BAD的平分线AE交BC于点E,连接DE.求证:四边形ABED是菱形.
D
A
B
C
E
1
2
3
尝试应用
菱形的判定例题
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
独立思考
可以用哪个判定方法呢?
尝试应用
菱形的判定例题
方法1:
证明:∵EF是AC的垂直平分线,
∴EA=EC,FA=FC,
AO=CO,∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO
∴△AOE≌△COF(ASA).
∴EA=FC.
∴EC=EA=FC=FA.
∴四边形AFCE是菱形.(四边相等的四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
尝试应用
菱形的判定例题
方法2:
证明:∵EF是AC的垂直平分线,
∴EA=EC,AO=CO,
∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∴△AOE≌△COF(ASA).
∴OE=OF.∴四边形AFCE是平行四边形.
又∵EA=EC,∴□AFCE是菱形.(有一组邻边相等的平行四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
尝试应用
菱形的判定例题
方法3:
证明:∵EF是AC的垂直平分线,
∴AC⊥EF,AO=CO,
∠AOE=∠COF=90°.
又∵□ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∴△AOE≌△COF(ASA).
∴OE=OF.∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴□AFCE是菱形.(对角线互相垂直的平行四边形是菱形)
例4:如图,□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形.
A
B
F
C
D
E
O
小结反思
本课小结
1.如何判定一个四边形为菱形?
2.解决判定菱形的问题最关键的是什么?
3.谈一谈你的收获与体会?
