人教版高中数学必修四 3.2简单的三角恒等变换 课件(共25张PPT)
文档属性
| 名称 | 人教版高中数学必修四 3.2简单的三角恒等变换 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 752.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-15 20:41:33 | ||
图片预览

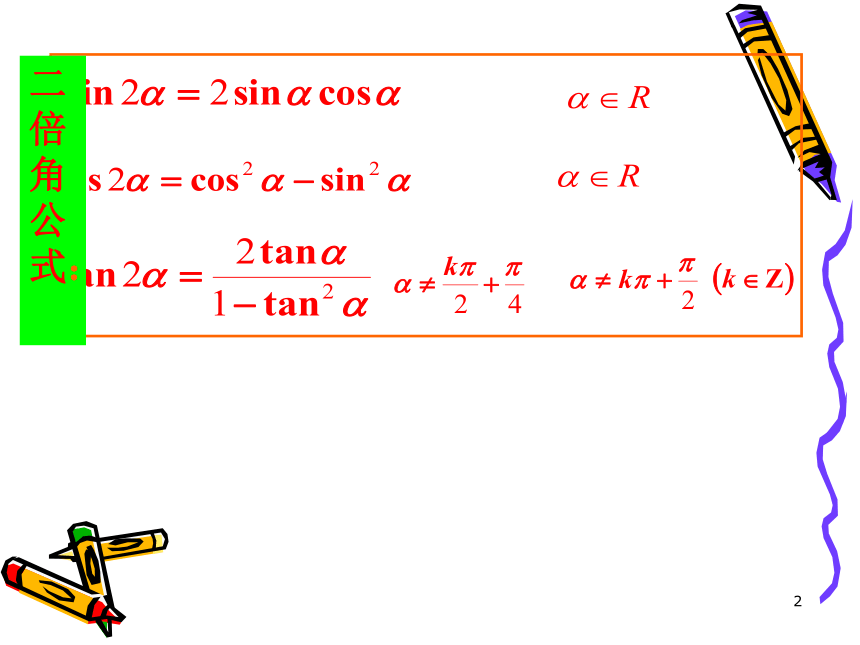
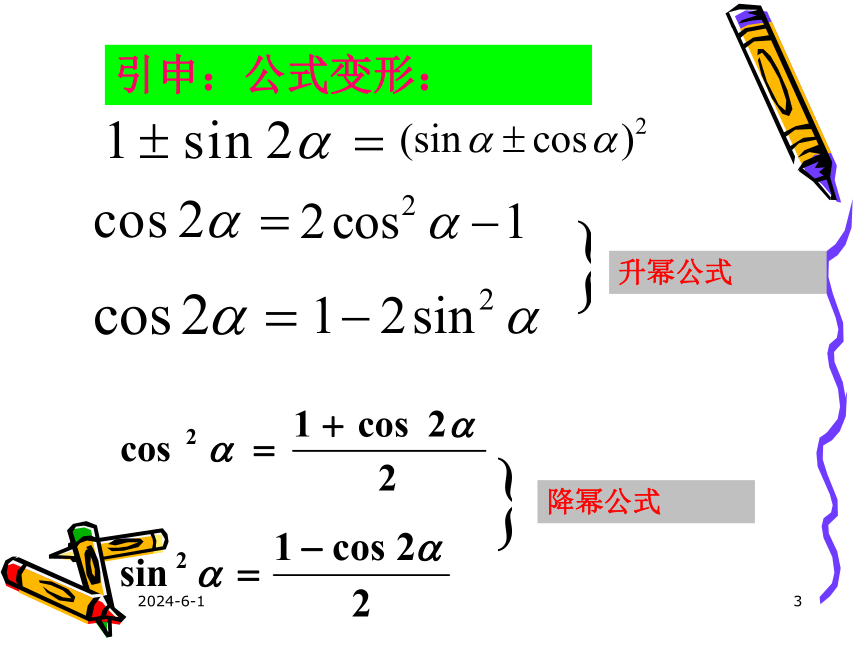
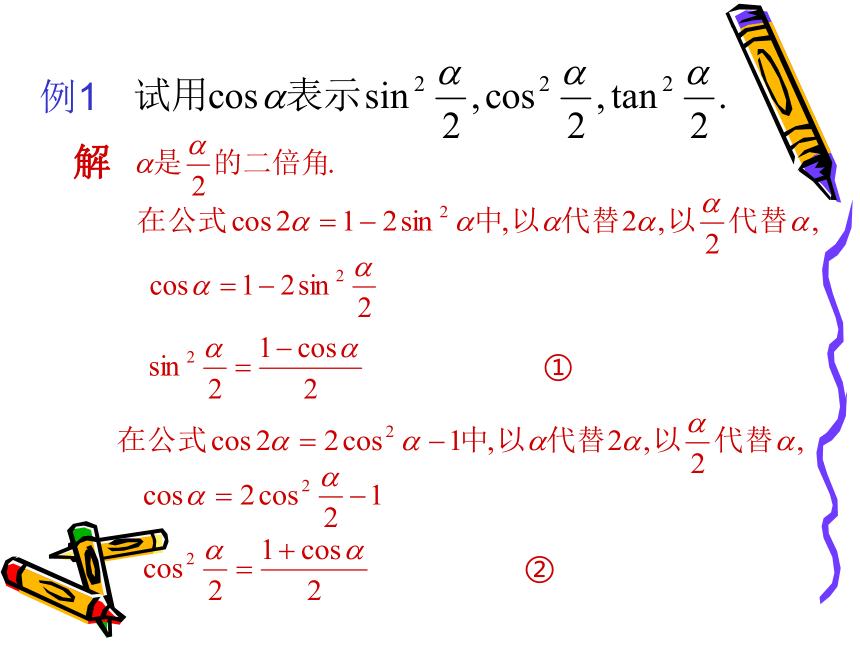
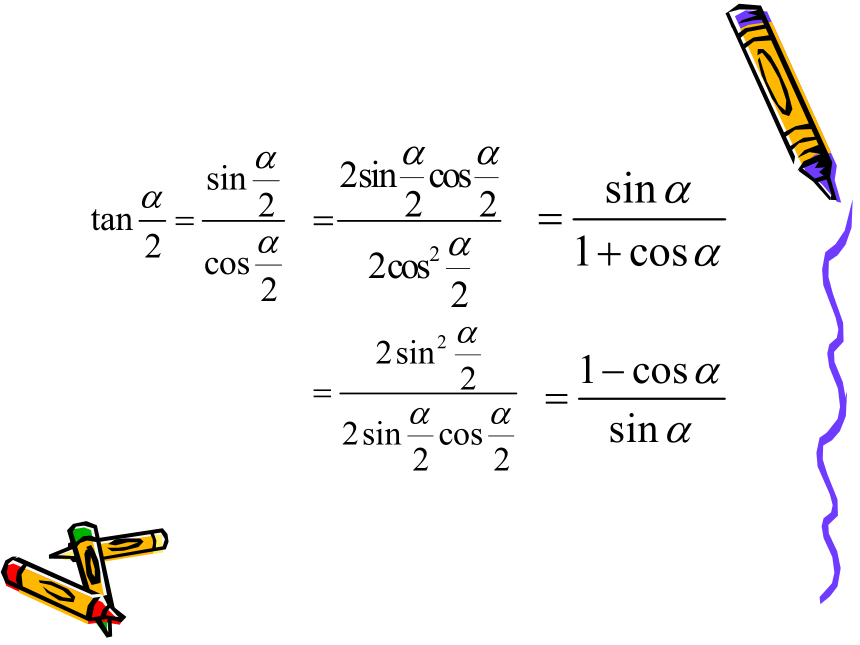
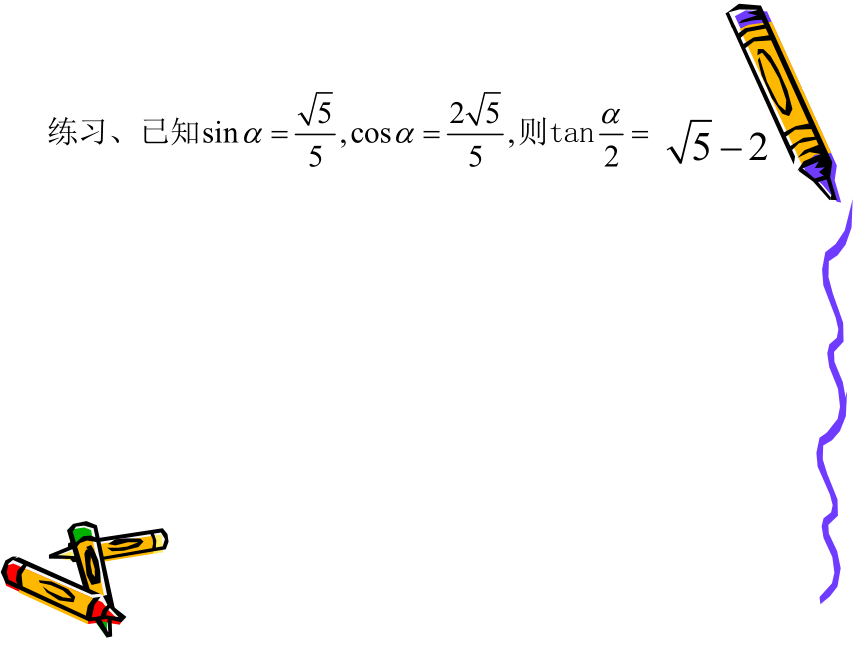

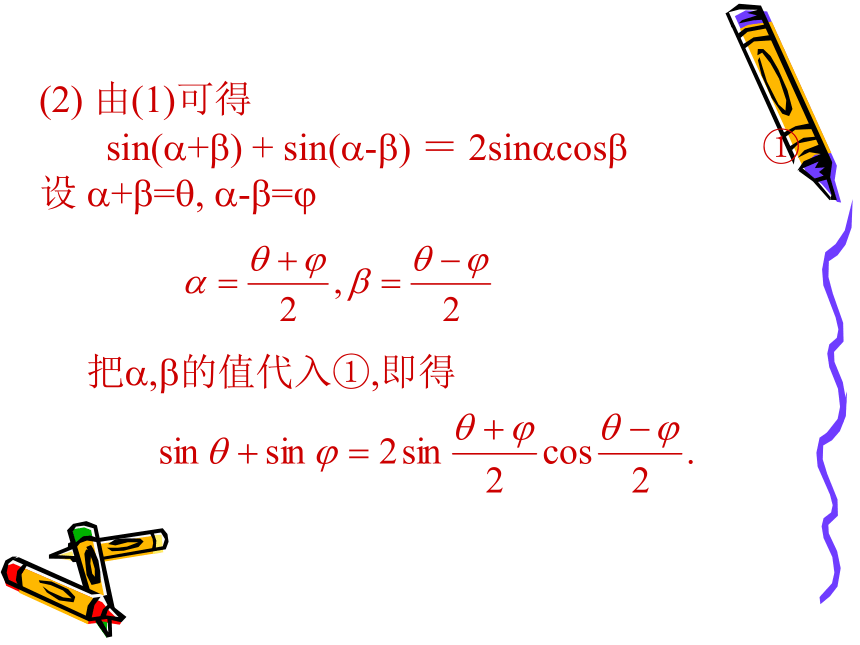
文档简介
(共25张PPT)
简单的三角恒等变换
*
二倍角公式:
*
*
引申:公式变形:
升幂公式
降幂公式
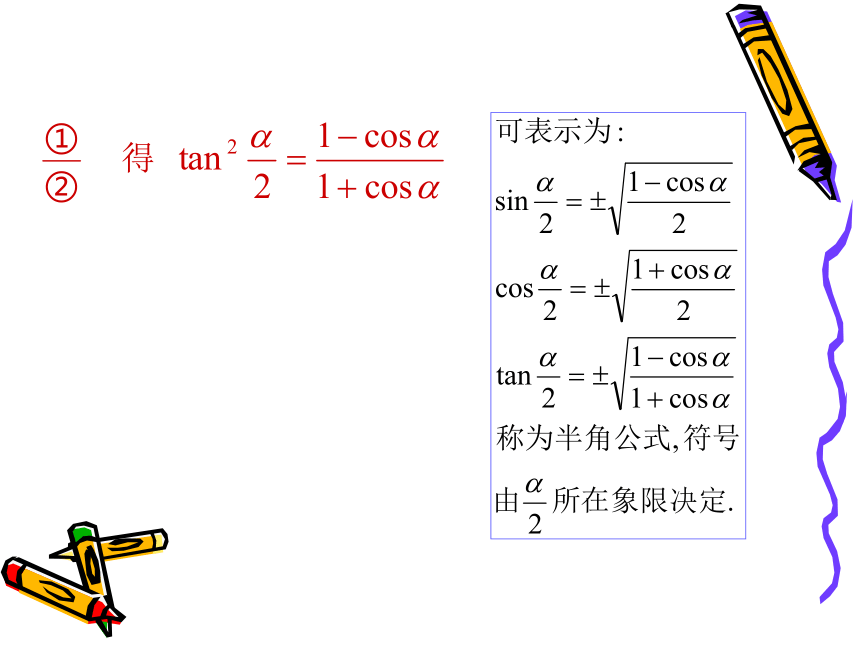
例1
解
例2 求证
解
(1) sin(?+?)和sin(?-?)是我们学过的知识,所以从右边着手
sin(?+?) = sin?cos?+cos?sin?
sin(?-?) = sin?cos?-cos?sin?
两式相加,得
sin(?+?) + sin(?-?) = 2sin?cos?
(2) 由(1)可得
sin(?+?) + sin(?-?) = 2sin?cos? ①
设 ?+?=?, ?-?=?
把?,?的值代入①,即得
例2证明中用到换元思想,
①式是积化和差的形式,
②式是和差化积的形式;
在后面的练习当中还有六个关于积化和差、和差化积的公式.
思考 在例2证明过程中用到了哪些数学思想方法?
例3
分析:利用三角恒等变换,先把函数式化简,再求相应的值.
解
所以,所求的周期为2??,最大值为2,最小值为-2.
点评:例3是三角恒等变换在数学中应用的举例,它使三角函数中对函数的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.
P143 A组5
例4
分析:要求当角?取何值时,矩形ABCD的面积S最大, 可分二步进行.
①找出S与?之间的函数关系;
②由得出的函数关系,求S的最大值.
解
在Rt△OBC中,OB=cos?,BC=sin?
在Rt△OAD中,
设矩形ABCD的面积为S,则
通过三角变换把形如y=asinx+bcosx的函数转化为形如y=Asin(??+?)的函数,从而使问题得到简化
题型一、化简求值问题
题型二、三角恒等式的证明
类型三、三角恒等变换与三角函数图像性质的综合
类型四、三角函数在实际问题中的应用
对变换过程中体现的换元、逆向使用公式等数学思想方法加深认识,学会灵活运用
小结
作业
课本第143页习题3.2A组
题1、(6)---(8).2
简单的三角恒等变换
*
二倍角公式:
*
*
引申:公式变形:
升幂公式
降幂公式
例1
解
例2 求证
解
(1) sin(?+?)和sin(?-?)是我们学过的知识,所以从右边着手
sin(?+?) = sin?cos?+cos?sin?
sin(?-?) = sin?cos?-cos?sin?
两式相加,得
sin(?+?) + sin(?-?) = 2sin?cos?
(2) 由(1)可得
sin(?+?) + sin(?-?) = 2sin?cos? ①
设 ?+?=?, ?-?=?
把?,?的值代入①,即得
例2证明中用到换元思想,
①式是积化和差的形式,
②式是和差化积的形式;
在后面的练习当中还有六个关于积化和差、和差化积的公式.
思考 在例2证明过程中用到了哪些数学思想方法?
例3
分析:利用三角恒等变换,先把函数式化简,再求相应的值.
解
所以,所求的周期为2??,最大值为2,最小值为-2.
点评:例3是三角恒等变换在数学中应用的举例,它使三角函数中对函数的性质研究得到延伸,体现了三角变换在化简三角函数式中的作用.
P143 A组5
例4
分析:要求当角?取何值时,矩形ABCD的面积S最大, 可分二步进行.
①找出S与?之间的函数关系;
②由得出的函数关系,求S的最大值.
解
在Rt△OBC中,OB=cos?,BC=sin?
在Rt△OAD中,
设矩形ABCD的面积为S,则
通过三角变换把形如y=asinx+bcosx的函数转化为形如y=Asin(??+?)的函数,从而使问题得到简化
题型一、化简求值问题
题型二、三角恒等式的证明
类型三、三角恒等变换与三角函数图像性质的综合
类型四、三角函数在实际问题中的应用
对变换过程中体现的换元、逆向使用公式等数学思想方法加深认识,学会灵活运用
小结
作业
课本第143页习题3.2A组
题1、(6)---(8).2
