人教A版数学必修二2.1空间点、直线、平面之间的位置关系(2)同步练习(含答案解析)
文档属性
| 名称 | 人教A版数学必修二2.1空间点、直线、平面之间的位置关系(2)同步练习(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 982.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:49:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.1空间点、直线、平面之间的位置关系(2)
一、选择题
如果OA∥O1A1,OB∥O1B1,那么∠AOB与∠A1O1B1( )
A. 相等 B. 互补 C. 相等或互补 D. 以上均不对
在三棱锥中,棱所在直线异面的有 )
A. 2对 B. 3对 C. 4对 D. 6对
正方体ABCD-A1B1C1D1中,与对角线A1B成45°的棱有( )条.
A. 4 B. 8 C. 12 D. 2
下列四个命题中错误的是( )
A. 若直线a、b互相平行,则直线a、b确定一个平面
B. 若四点不共面,则这四点中任意三点都不共线
C. 若两条直线没有公共点,则这两条直线是异面直线
D. 两条异面直线不可能垂直于同一个平面
异面直线是指( )
A. 空间中两条不相交的直线
B. 平面内的一条直线与平面外的一条直线
C. 分别位于两个不同平面内的两条直线
D. 不同在任何一个平面内的两条直线
两直线l1与l2异面,过l1作平面与l2平行,这样的平面( ).
A. 不存在 B. 有唯一的一个 C. 有无数个 D. 只有两个
如图,在直三棱柱ABC-A1B1C1的棱所在的直线中,与直线BC1异面的直线的条数为( )
A. 1
B. 2
C. 3
D. 4
若直线、平行,直线、异面,则直线、的位置关系是(???? )
A. 异面 B. 相交 C. 平行 D. 相交或异面
二、填空题
如果两条直线a和b没有公共点,那么a与b的位置关系是______.
如图,正方体中,M、N分别为棱、的中点,有以下四个结论:
直线AM与是相交直线;
直线AM与BN是平行直线;
直线BN与是异面直线;
直线AM与是异面直线.
其中正确的结论为______注:把你认为正确的结论的序号都填上.
三、解答题
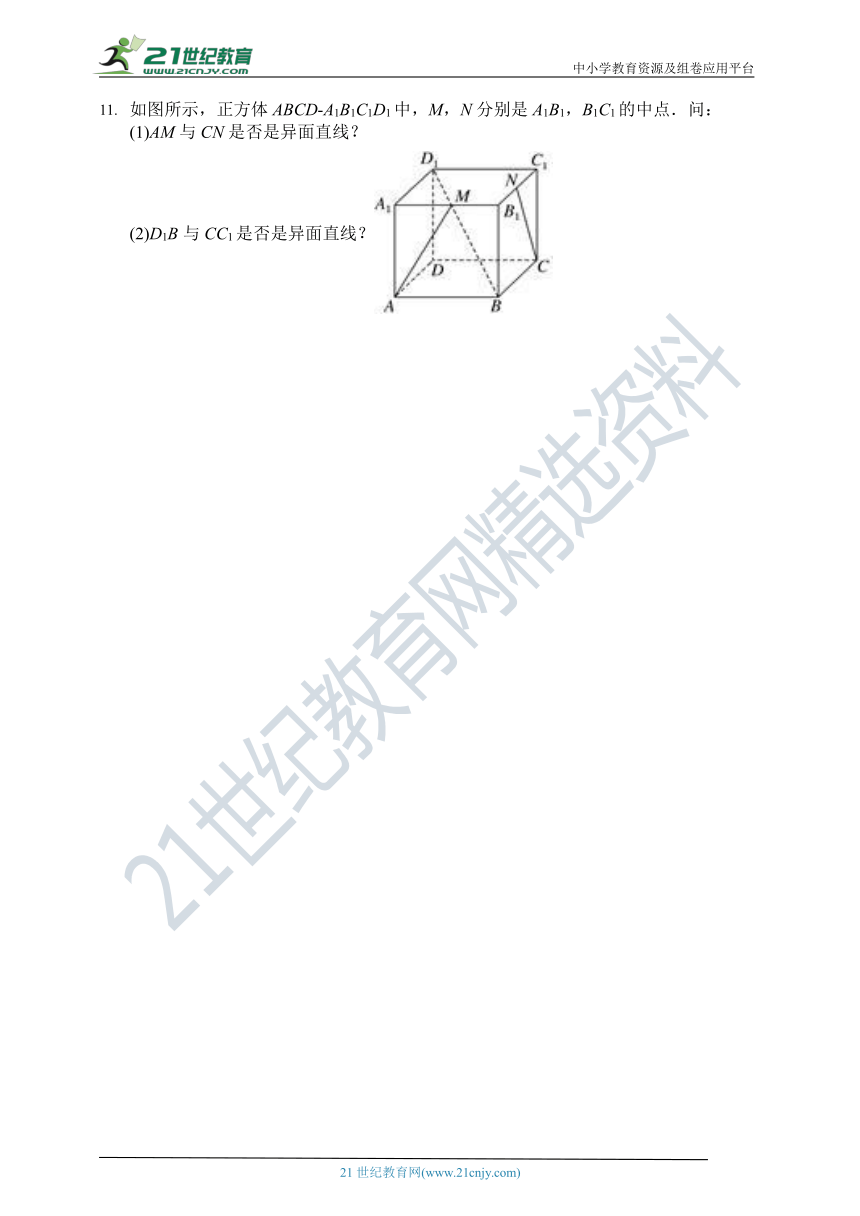
如图所示,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:
(1)AM与CN是否是异面直线?
(2)D1B与CC1是否是异面直线?
答案和解析
1.C解:若∠AOB与∠A′O′B′方向相同.则∠AOB=∠A′O′B′;
若∠AOB与∠A′O′B′方向相反,则∠AOB+∠A′O′B′=180°.
? 2.B解:如图所示,三棱锥P-ABC中,棱PA与BC是异面直线,棱PB与AC是异面直线,棱PC与AB是异面直线;共3对.
3.B解:如图所示:
在正方形ABB1A1中,AA1、AB、BB1、A1B1与A1B均成45°角,
根据线线角的定义知,DD1、CC1、DC、D1C1都与A1B成45°角,
所以满足条件的棱有8条,
4.C
解:A、由两条直线平行确定一个平面判断正确,故A不对;
B、根据三棱锥的四个顶点知,任意三点都不共线,故B不对;
C、若两条直线没有公共点,则这两条直线异面或平行,故C对;
D、根据线面垂直的性质定理知,这两条直线平行,即不可能,故D不对.
5.D解:A 不正确,因为空间中两条不相交的直线可能平行.
B 不正确,因为平面内的一条直线与平面外的一条直线可能平行,也可能相交.
C不正确,因为分别位于两个不同平面内的两条直线可能平行,也可能相交.
D 正确,这就是异面直线的定义. 故选 D.
6.B解:在l1上取一点,做直线a,使得a∥l2, 因为l1与a相交,所以确定一个平面, 又因为a∥l2, 所以l2平行这个平面, 由公理三知满足条件的平面有且只有一个.
7.C解:在直三棱柱ABC-A1B1C1的棱所在的直线中,
与直线BC1异面的直线有:A1B1,AC,AA1,共3条.
8.D解:在正方体ABCD-A1B1C1D1中,
?取AB=a,CD=b,当为c时,满足b,c是平行直线,此时直线a,c相交;
? 当A1D1为c时,满足b,c是异面直线,直线b∥a,此时直线c与a是异面直线.?
∴若a,b是平行直线,直线b,c异面,则a与c的位置关系是异面或相交.?
9.平行或异面 解:空间中两条直线的位置关系有三种:
相交,有且只有一个公共点;平行,没有公共点; 异面,没有公共点.
由此可知,如果两条直线a和b没有公共点,
那么a与b的位置关系是平行或异面. 故答案为:平行或异面.
10.?解:、M、C、四点不共面直线AM与是异面直线,故错误;同理,直线AM与BN也是异面直线,故错误.同理,直线BN与是异面直线,故正确;同理,直线AM与是异面直线,故正确;故答案为.
11.解:(1)AM,CN不是异面直线;
(2)直线D1B和CC1是异面直线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.1空间点、直线、平面之间的位置关系(2)
一、选择题
如果OA∥O1A1,OB∥O1B1,那么∠AOB与∠A1O1B1( )
A. 相等 B. 互补 C. 相等或互补 D. 以上均不对
在三棱锥中,棱所在直线异面的有 )
A. 2对 B. 3对 C. 4对 D. 6对
正方体ABCD-A1B1C1D1中,与对角线A1B成45°的棱有( )条.
A. 4 B. 8 C. 12 D. 2
下列四个命题中错误的是( )
A. 若直线a、b互相平行,则直线a、b确定一个平面
B. 若四点不共面,则这四点中任意三点都不共线
C. 若两条直线没有公共点,则这两条直线是异面直线
D. 两条异面直线不可能垂直于同一个平面
异面直线是指( )
A. 空间中两条不相交的直线
B. 平面内的一条直线与平面外的一条直线
C. 分别位于两个不同平面内的两条直线
D. 不同在任何一个平面内的两条直线
两直线l1与l2异面,过l1作平面与l2平行,这样的平面( ).
A. 不存在 B. 有唯一的一个 C. 有无数个 D. 只有两个
如图,在直三棱柱ABC-A1B1C1的棱所在的直线中,与直线BC1异面的直线的条数为( )
A. 1
B. 2
C. 3
D. 4
若直线、平行,直线、异面,则直线、的位置关系是(???? )
A. 异面 B. 相交 C. 平行 D. 相交或异面
二、填空题
如果两条直线a和b没有公共点,那么a与b的位置关系是______.
如图,正方体中,M、N分别为棱、的中点,有以下四个结论:
直线AM与是相交直线;
直线AM与BN是平行直线;
直线BN与是异面直线;
直线AM与是异面直线.
其中正确的结论为______注:把你认为正确的结论的序号都填上.
三、解答题
如图所示,正方体ABCD-A1B1C1D1中,M,N分别是A1B1,B1C1的中点.问:
(1)AM与CN是否是异面直线?
(2)D1B与CC1是否是异面直线?
答案和解析
1.C解:若∠AOB与∠A′O′B′方向相同.则∠AOB=∠A′O′B′;
若∠AOB与∠A′O′B′方向相反,则∠AOB+∠A′O′B′=180°.
? 2.B解:如图所示,三棱锥P-ABC中,棱PA与BC是异面直线,棱PB与AC是异面直线,棱PC与AB是异面直线;共3对.
3.B解:如图所示:
在正方形ABB1A1中,AA1、AB、BB1、A1B1与A1B均成45°角,
根据线线角的定义知,DD1、CC1、DC、D1C1都与A1B成45°角,
所以满足条件的棱有8条,
4.C
解:A、由两条直线平行确定一个平面判断正确,故A不对;
B、根据三棱锥的四个顶点知,任意三点都不共线,故B不对;
C、若两条直线没有公共点,则这两条直线异面或平行,故C对;
D、根据线面垂直的性质定理知,这两条直线平行,即不可能,故D不对.
5.D解:A 不正确,因为空间中两条不相交的直线可能平行.
B 不正确,因为平面内的一条直线与平面外的一条直线可能平行,也可能相交.
C不正确,因为分别位于两个不同平面内的两条直线可能平行,也可能相交.
D 正确,这就是异面直线的定义. 故选 D.
6.B解:在l1上取一点,做直线a,使得a∥l2, 因为l1与a相交,所以确定一个平面, 又因为a∥l2, 所以l2平行这个平面, 由公理三知满足条件的平面有且只有一个.
7.C解:在直三棱柱ABC-A1B1C1的棱所在的直线中,
与直线BC1异面的直线有:A1B1,AC,AA1,共3条.
8.D解:在正方体ABCD-A1B1C1D1中,
?取AB=a,CD=b,当为c时,满足b,c是平行直线,此时直线a,c相交;
? 当A1D1为c时,满足b,c是异面直线,直线b∥a,此时直线c与a是异面直线.?
∴若a,b是平行直线,直线b,c异面,则a与c的位置关系是异面或相交.?
9.平行或异面 解:空间中两条直线的位置关系有三种:
相交,有且只有一个公共点;平行,没有公共点; 异面,没有公共点.
由此可知,如果两条直线a和b没有公共点,
那么a与b的位置关系是平行或异面. 故答案为:平行或异面.
10.?解:、M、C、四点不共面直线AM与是异面直线,故错误;同理,直线AM与BN也是异面直线,故错误.同理,直线BN与是异面直线,故正确;同理,直线AM与是异面直线,故正确;故答案为.
11.解:(1)AM,CN不是异面直线;
(2)直线D1B和CC1是异面直线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
