人教A版数学必修二2.2直线、平面平行的判定及其性质(1)同步练习(含答案)
文档属性
| 名称 | 人教A版数学必修二2.2直线、平面平行的判定及其性质(1)同步练习(含答案) |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 14:12:36 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.2直线、平面平行的判定及其性质(1)
一、单选题
1.如图,在三棱锥P-ABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则AB与GH的关系是 ( )
A.平行 B.垂直 C.异面D.平行或垂直
2.正方体ABCD-A1B1C1D1中,截面BA1C1与直线AC的位置关系是 ( )
A.AC∥截面BA1C1 B.AC与截面BA1C1相交
C.AC在截面BA1C1内 D.以上答案都错误
3.一正方体表面沿着几条棱裁开放平得到如图所示的展开图,则在原正方体中( )
A. B. C. D.
4.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( )
A.0 B.1 C.2 D.3
5.下列说法正确的是( )
A.若直线l平行于平面α内的无数条直线,则l∥α B.若直线a在平面α外,则a∥α
C.若直线a∥b,b?α,则a∥α D.若直线a∥b,b?α,那么直线a平行于α内的无数条直线
6.在空间四边形中,E,F分别是AB和BC上的点,若,则对角线AC和平面DEF的位置关系是( )
A.平行 B.相交 C.在平面内 D.异面
7.在空间四边形ABCD中,E、F分别为AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则 ( )
A.BD//平面EFGH且EFGH为矩形 B.EF//平面BCD且EFGH为梯形
C.HG//平面ABD且EFGH为菱形 D.HE//平面ADC且EFGH是平行四边形
8.在正方体ABCD?A1B1C1D1中,棱长为a,M,N分别为A1B,AC的中点,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行 C.垂直 D.不能确定
二、填空题
9.以下命题(其中表示直线,表示平面)
①若,则 ②若,,则
③若,,则 ④若,,则
其中正确命题的个数是 ______________________.
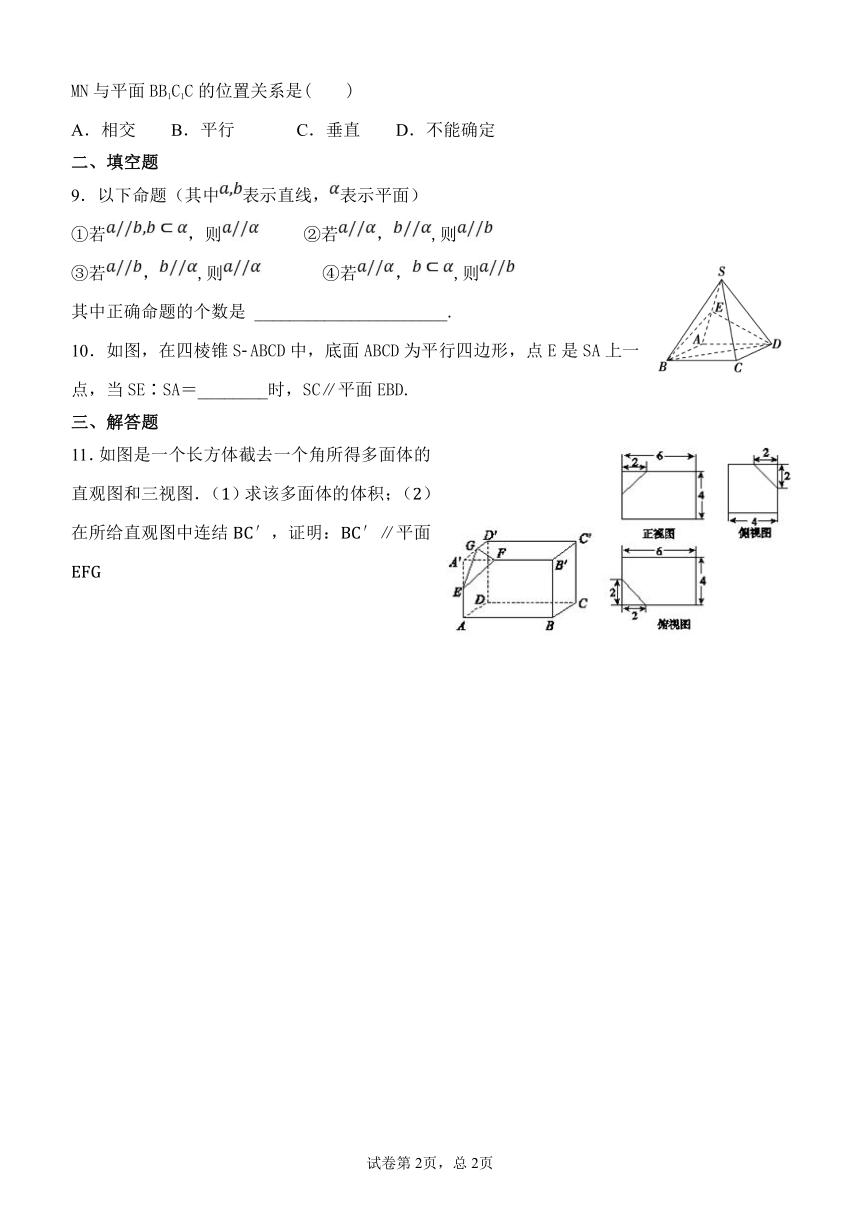
10.如图,在四棱锥S?ABCD中,底面ABCD为平行四边形,点E是SA上一点,当SE∶SA=________时,SC∥平面EBD.
三、解答题
11.如图是一个长方体截去一个角所得多面体的直观图和三视图.(1)求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥平面EFG
试卷第2页,总2页
试卷第1页,总2页
参考答案
1.A 2.A
3.C原正方体如图,由图可得CD∥GH,C正确.AB与CD相交,A错误;AB与平面CD 相交,B错误;AB与GH是异面直线,D错误.
4.C
在△ACD中,∵G,F分别为AD与CD的中点,∴GF∥AC.而GF?平面EFG,
∴AC∥平面EFG.同理,BD∥平面EFG.故选:C.
5.D 6.A
7.B因为AE∶EB=AF∶FD=1∶4所以∽ ,且
因为 所以又因为H、G分别为BC、CD的中点
所以,根据平行线的性质可知
所以四边形EFGH为梯形
8.B
9.0
①要想,还需要这个条件,故本命题是假命题;
②除了平行以外还可以相交,异面,故本命题是假命题;
③还存在这种可能性,故本命题是假命题;
④可以是两条异面直线,故本命题是假命题,因此正确的命题的个数为零.
10.
由题意,连接AC交BD于O,连接EO,当EO平行SC,及E为SA中点时,SC∥平面EBD,故得结论.
如图,连接AC,设AC与BD的交点为O,连接EO.
因为四边形ABCD是平行四边形,所以点O是AC的中点.
因为SC∥平面EBD,且平面EBD∩平面SAC=EO,所以SC∥EO,
所以点E是SA的中点,此时SE∶SA=1∶2.
18.(1);(2)V=V长方体-V正三棱锥==;
(2)证明:在长方体ABCD-A'B'C'D'中,连结AD',则AD'∥BC'.因为E,G分别为AA',A'D'中点,
所以AD'∥EG,从而EG∥BC'.又BC'平面EFG,EG平面EFG,所以BC'∥面EFG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2直线、平面平行的判定及其性质(1)
一、单选题
1.如图,在三棱锥P-ABQ中,D,C,E,F分别是AQ,BQ,AP,BP的中点,PD与EQ交于点G,PC与FQ交于点H,连接GH,则AB与GH的关系是 ( )
A.平行 B.垂直 C.异面D.平行或垂直
2.正方体ABCD-A1B1C1D1中,截面BA1C1与直线AC的位置关系是 ( )
A.AC∥截面BA1C1 B.AC与截面BA1C1相交
C.AC在截面BA1C1内 D.以上答案都错误
3.一正方体表面沿着几条棱裁开放平得到如图所示的展开图,则在原正方体中( )
A. B. C. D.
4.E,F,G分别是空间四边形ABCD的棱BC,CD,DA的中点,则此四面体中与过E,F,G的截面平行的棱的条数是( )
A.0 B.1 C.2 D.3
5.下列说法正确的是( )
A.若直线l平行于平面α内的无数条直线,则l∥α B.若直线a在平面α外,则a∥α
C.若直线a∥b,b?α,则a∥α D.若直线a∥b,b?α,那么直线a平行于α内的无数条直线
6.在空间四边形中,E,F分别是AB和BC上的点,若,则对角线AC和平面DEF的位置关系是( )
A.平行 B.相交 C.在平面内 D.异面
7.在空间四边形ABCD中,E、F分别为AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则 ( )
A.BD//平面EFGH且EFGH为矩形 B.EF//平面BCD且EFGH为梯形
C.HG//平面ABD且EFGH为菱形 D.HE//平面ADC且EFGH是平行四边形
8.在正方体ABCD?A1B1C1D1中,棱长为a,M,N分别为A1B,AC的中点,则MN与平面BB1C1C的位置关系是( )
A.相交 B.平行 C.垂直 D.不能确定
二、填空题
9.以下命题(其中表示直线,表示平面)
①若,则 ②若,,则
③若,,则 ④若,,则
其中正确命题的个数是 ______________________.
10.如图,在四棱锥S?ABCD中,底面ABCD为平行四边形,点E是SA上一点,当SE∶SA=________时,SC∥平面EBD.
三、解答题
11.如图是一个长方体截去一个角所得多面体的直观图和三视图.(1)求该多面体的体积;(2)在所给直观图中连结BC′,证明:BC′∥平面EFG
试卷第2页,总2页
试卷第1页,总2页
参考答案
1.A 2.A
3.C原正方体如图,由图可得CD∥GH,C正确.AB与CD相交,A错误;AB与平面CD 相交,B错误;AB与GH是异面直线,D错误.
4.C
在△ACD中,∵G,F分别为AD与CD的中点,∴GF∥AC.而GF?平面EFG,
∴AC∥平面EFG.同理,BD∥平面EFG.故选:C.
5.D 6.A
7.B因为AE∶EB=AF∶FD=1∶4所以∽ ,且
因为 所以又因为H、G分别为BC、CD的中点
所以,根据平行线的性质可知
所以四边形EFGH为梯形
8.B
9.0
①要想,还需要这个条件,故本命题是假命题;
②除了平行以外还可以相交,异面,故本命题是假命题;
③还存在这种可能性,故本命题是假命题;
④可以是两条异面直线,故本命题是假命题,因此正确的命题的个数为零.
10.
由题意,连接AC交BD于O,连接EO,当EO平行SC,及E为SA中点时,SC∥平面EBD,故得结论.
如图,连接AC,设AC与BD的交点为O,连接EO.
因为四边形ABCD是平行四边形,所以点O是AC的中点.
因为SC∥平面EBD,且平面EBD∩平面SAC=EO,所以SC∥EO,
所以点E是SA的中点,此时SE∶SA=1∶2.
18.(1);(2)V=V长方体-V正三棱锥==;
(2)证明:在长方体ABCD-A'B'C'D'中,连结AD',则AD'∥BC'.因为E,G分别为AA',A'D'中点,
所以AD'∥EG,从而EG∥BC'.又BC'平面EFG,EG平面EFG,所以BC'∥面EFG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
