人教版高中数学选修4-6 第二讲 同余与同余方程 二 剩余类及其运算 上课课件(共30张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第二讲 同余与同余方程 二 剩余类及其运算 上课课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 467.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
知识回顾
试写出1到20之间所以的偶数集,所以的奇数集.
偶数集
{2、4、6、8、10、12、14、16、18、20}
奇数集
{1、5、5、7、9、11、13、15、17、19}
集合定义记得吗
某些指定的对象集在一起就成为一个集合
导入新课
在前一节的学习中我们已经知道了同余的概念.
由同余的概念想一下,按模3是否同余,对1到10的数可以分成什么样的集合呢.
想一下模8的余数都可能是哪些?
模8的余数不能大于等于8,所以模8的余数可能是0、1、2、3、4、5、6、7.
想一想模n的余数有哪些情况呢
想一想模n的可能的余数有哪些?你能否将整数按模n同余,n的所有的可能的余数写成集合.
第二讲 同余与同余方程
第二节 剩余类及其运算
教学目标
知识与能力
1.掌握模m的剩余类及完全剩余系的概念.
2.理解模m的最小非负剩余系,完全剩余系的性质.
3.熟练运用判断剩余系的方法.
过程与方法
情感态度与价值观
1.通过对学习过的知识的复习引出剩余类的概念.
2.类比整数运算法则,推导出剩余类的运算性质.
培养学以致用的精神,将理论应用与现实生活.
教学重难点
重 点
难 点
1.理解剩余类的概念.
2.体会剩余类加法、乘法运算与整数的加法、乘法之间的联系与差别.
剩余类的概念及其运算.
我们知道若一个整数n做除数那么它的余数一定小于n,如5做除数,那么余数可能是0、1、2、3、4这五种情况.
这样按模n是否同余,可以对一组数,甚至是整数集进行分类.
议一议
实例
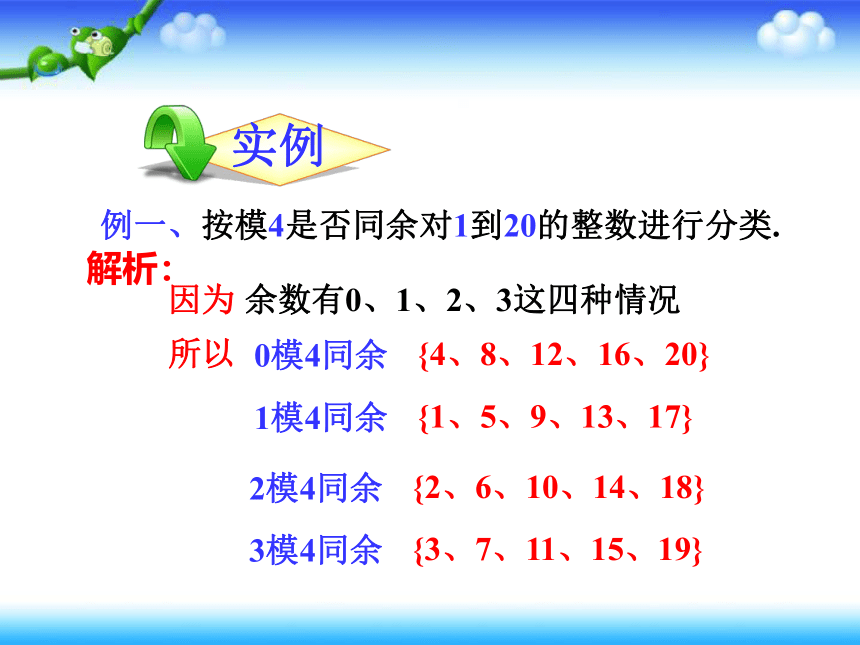
例一、按模4是否同余对1到20的整数进行分类.
解析:
因为 余数有0、1、2、3这四种情况
所以
0模4同余
{4、8、12、16、20}
1模4同余
{1、5、9、13、17}
2模4同余
{2、6、10、14、18}
3模4同余
{3、7、11、15、19}
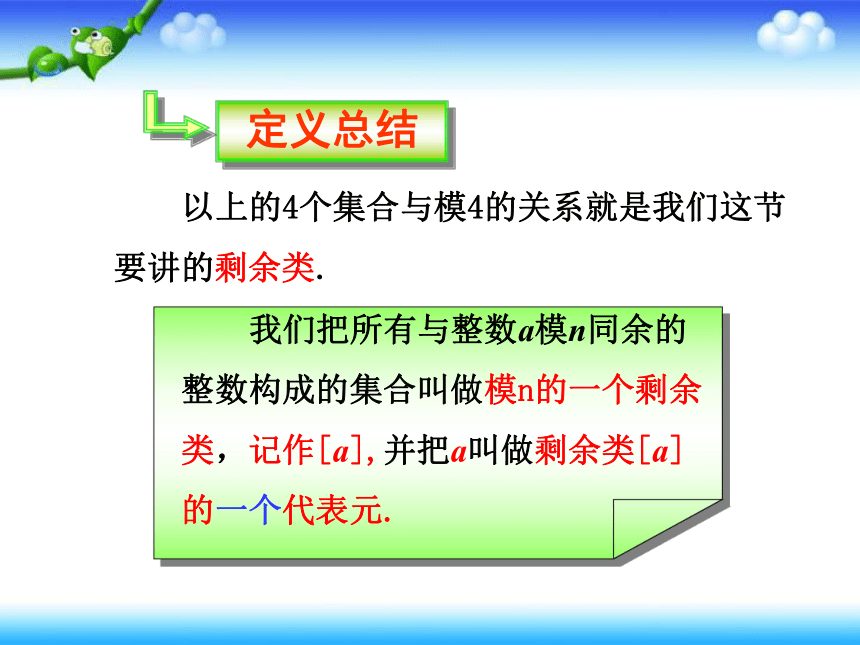
以上的4个集合与模4的关系就是我们这节要讲的剩余类.
定义总结
我们把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类,记作[a],并把a叫做剩余类[a]的一个代表元.
分析
依定义,在例一中模4的不同剩余类共有4个,它们分别表示为[0]、 [1]、 [2]、 [3];
注意:在定义中剩余类可以用不同的代表元来表示.
如例一:[0]=[4]=[8]=[12]=[16]=[20]
分析
在整数中有加法、乘法运算,剩余类是否有同样的运算呢?
思考
在例一中
[5]+[9]=[5+9]
[2]+[11]=[2+11]
[2]+[12]=[2+12]
[13]+[3]=[13+3]
[2][6]=[2·12]
[3][4]=[3·4]
[2][5]=[2·5]
[3][5]=[3·5]
从以上的分析中,我们可以总结出
剩余类加法:[a]+[b]=[a +b]
剩余类乘法:[a][b]=[a ·b]
把含有剩余类加法运算、乘法运算的模n的剩余类集合叫做模n的剩余环.
自己举例验证一下上面的性质.
观察例一分析得
[3]([2]+ [3]) ( ) [3][2]+[3][3]
[2]+[12] ( ) [12]+[2]
[3]+[11] ( ) [11]+[3]
=
=
=
结论:
剩余类遵循交换律、结合律、分配律.
由剩余类的运算性质我们得到:
[a]+ [0] = [0]+[a] = [a]
[a][0] = [0][a] = [0]
[a][1] = [1][a] = [a]
单位元
零元
[a]+ [b] = [b]+[a] = [0]
[b]是[a]的逆元.
若:[a][b] = [b][a] = [1]
[b]是[a]的负元.
推论
议一议
是不是整数的加法、乘法运算法则都适用于剩余类环呢.
在整数乘法中若 a≠0,b ≠0,那么ab ≠0
在剩余类环乘法中,对模6的剩余类乘法[2]≠0, [3] ≠0,但是[3] [2]=0.
并非所有整数的运算法则都适用于剩余环.
课堂小结
1、剩余类的概念:模n同余的所有整数集合.
2、剩余类的表示:剩余类的任何代表元均可代表.
3、剩余类的实质:剩余类实质是一个集合.
4、剩余类的运算法则:
剩余类加法:[a]+[b]=[a +b]
剩余类乘法:[a][b]=[a ·b]
5、剩余类的定义:剩余类集合中定义了加法和剩余类乘法运算.
{[0],[1],,…… ,[n-1],+, ·}
6、剩余类环的特殊元素:
零元:[0],单位元[1]
7、剩余类间的相互关系:
[a]+ [b] = [b]+[a] = [0]
[b]是[a]的逆元.
[a][b] = [b][a] = [1]
[b]是[a]的负元.
则展开式的常数项为( )
针对性练习
2、设实数a≠0,{an}是以a为首项,-a为公比的等比数列,且bn=anlg|an|(nN),问当0
展开式的二项式系数之和为64,
1、
20
思考和分析 初看题目似乎很难下手,但只要我们冷静想一想,不妨假设存在m0 N,使对任意n N,都有bn bm0,也就是说bm0应该是数列{bn}的最大项,这样我们将问题化归为数列{bn}的最大项的存在性问题,从而就容易入手了.
3、???????????????????????????????????????????? 则A、B、C的关系是?
【解析】要判断集合A、B、C之间的关系,可以对每个集合中元素所满足的条件进行变形整理,然后找出条件式子结构的差异,最后只需比较这些“差异”就可以了.本试题中,
据整数剩余类知识知,3(n-1)+1(n∈Z)和3p+1都表示被3除余1的整数, 因而知B=C.又p∈Z,则令 知 ??????????
故 【点评】因为6m+1(m∈Z)表示被6除余1的整数,且为奇数;而3p+1(p∈Z)表示被
A ??B=C
3整除余1的整数,它可能是偶数,也可能是奇数,为了寻找集合A与C的关系,必须明确3p+1(p∈Z)何时为奇数以及奇数的类型,为此只需把p分类奇数和偶数即可.
辛苦~\(≧▽≦)/~啦啦啦
课堂练习
2、一个数被3除余2,被7除余4,被8除余5,这个数最小是( )
3、一个数除以5余4,除以8余3,除以11余2,满足条件的最小的自然数( ).
1、一年级同学,每9人一排多5人,每7人一排多1人,每5人一排多2人,至少有多少人( )
302
53
A.302 B.299 C.201 D.401
B
解:〔4,5〕=20;〔3,5〕=15;〔3,4〕=12;〔3,4,5〕=60.为了使20被3除余1,用20×2=40;使15被4除余1,用15×3=45;使12被5除余1,用12×3=36.然后,40×1+45×2+36×4=274,因为,274>60,所以,274-60×4=34,就是所求的数.
5、被3除余1,被4除余2,被5除余4,这个数最小是?
4、9人一排多6人,7人一排多2人,5人一排多3人,至少( )人 .
A.303 B.299 C.202 D.405
A
6、模m=10,根据余数可以将所有整数分成10个类别
[0]即 C0={c| c mod m=0 mod m}
={c| c mod 10=0 mod 10}
={c| c mod 10=0}={c|c=t?10}
={0,10,20,30,40,50,…,-10,-20,…}
[1]即 C1={c| c mod m=1 mod m}
={c| c mod m=1}={c| c=s?10+1}
={1,11,21,31,41,…,-11,-21,-31,…}
[a]即Ca={c| c mod m=a mod m} (a<10)
={c| c mod 10=a }
={c| c=k?10+a}
7、证明:不存在整数a、b、c,满足a2+b2-8c=6
证明 由于每个整数都具有下列形式之一4n,4n1,4n+2,
它们的平方数分别是:16n2,16n28n+1,16n2+16n+4,
它们被8除的余数分别是:0,1,4.而这三个余数的任意两数(可以相同)的和都不等于6,所以对任意整数a、b、c,a2+b2-8c=6.
再见
知识回顾
试写出1到20之间所以的偶数集,所以的奇数集.
偶数集
{2、4、6、8、10、12、14、16、18、20}
奇数集
{1、5、5、7、9、11、13、15、17、19}
集合定义记得吗
某些指定的对象集在一起就成为一个集合
导入新课
在前一节的学习中我们已经知道了同余的概念.
由同余的概念想一下,按模3是否同余,对1到10的数可以分成什么样的集合呢.
想一下模8的余数都可能是哪些?
模8的余数不能大于等于8,所以模8的余数可能是0、1、2、3、4、5、6、7.
想一想模n的余数有哪些情况呢
想一想模n的可能的余数有哪些?你能否将整数按模n同余,n的所有的可能的余数写成集合.
第二讲 同余与同余方程
第二节 剩余类及其运算
教学目标
知识与能力
1.掌握模m的剩余类及完全剩余系的概念.
2.理解模m的最小非负剩余系,完全剩余系的性质.
3.熟练运用判断剩余系的方法.
过程与方法
情感态度与价值观
1.通过对学习过的知识的复习引出剩余类的概念.
2.类比整数运算法则,推导出剩余类的运算性质.
培养学以致用的精神,将理论应用与现实生活.
教学重难点
重 点
难 点
1.理解剩余类的概念.
2.体会剩余类加法、乘法运算与整数的加法、乘法之间的联系与差别.
剩余类的概念及其运算.
我们知道若一个整数n做除数那么它的余数一定小于n,如5做除数,那么余数可能是0、1、2、3、4这五种情况.
这样按模n是否同余,可以对一组数,甚至是整数集进行分类.
议一议
实例
例一、按模4是否同余对1到20的整数进行分类.
解析:
因为 余数有0、1、2、3这四种情况
所以
0模4同余
{4、8、12、16、20}
1模4同余
{1、5、9、13、17}
2模4同余
{2、6、10、14、18}
3模4同余
{3、7、11、15、19}
以上的4个集合与模4的关系就是我们这节要讲的剩余类.
定义总结
我们把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类,记作[a],并把a叫做剩余类[a]的一个代表元.
分析
依定义,在例一中模4的不同剩余类共有4个,它们分别表示为[0]、 [1]、 [2]、 [3];
注意:在定义中剩余类可以用不同的代表元来表示.
如例一:[0]=[4]=[8]=[12]=[16]=[20]
分析
在整数中有加法、乘法运算,剩余类是否有同样的运算呢?
思考
在例一中
[5]+[9]=[5+9]
[2]+[11]=[2+11]
[2]+[12]=[2+12]
[13]+[3]=[13+3]
[2][6]=[2·12]
[3][4]=[3·4]
[2][5]=[2·5]
[3][5]=[3·5]
从以上的分析中,我们可以总结出
剩余类加法:[a]+[b]=[a +b]
剩余类乘法:[a][b]=[a ·b]
把含有剩余类加法运算、乘法运算的模n的剩余类集合叫做模n的剩余环.
自己举例验证一下上面的性质.
观察例一分析得
[3]([2]+ [3]) ( ) [3][2]+[3][3]
[2]+[12] ( ) [12]+[2]
[3]+[11] ( ) [11]+[3]
=
=
=
结论:
剩余类遵循交换律、结合律、分配律.
由剩余类的运算性质我们得到:
[a]+ [0] = [0]+[a] = [a]
[a][0] = [0][a] = [0]
[a][1] = [1][a] = [a]
单位元
零元
[a]+ [b] = [b]+[a] = [0]
[b]是[a]的逆元.
若:[a][b] = [b][a] = [1]
[b]是[a]的负元.
推论
议一议
是不是整数的加法、乘法运算法则都适用于剩余类环呢.
在整数乘法中若 a≠0,b ≠0,那么ab ≠0
在剩余类环乘法中,对模6的剩余类乘法[2]≠0, [3] ≠0,但是[3] [2]=0.
并非所有整数的运算法则都适用于剩余环.
课堂小结
1、剩余类的概念:模n同余的所有整数集合.
2、剩余类的表示:剩余类的任何代表元均可代表.
3、剩余类的实质:剩余类实质是一个集合.
4、剩余类的运算法则:
剩余类加法:[a]+[b]=[a +b]
剩余类乘法:[a][b]=[a ·b]
5、剩余类的定义:剩余类集合中定义了加法和剩余类乘法运算.
{[0],[1],,…… ,[n-1],+, ·}
6、剩余类环的特殊元素:
零元:[0],单位元[1]
7、剩余类间的相互关系:
[a]+ [b] = [b]+[a] = [0]
[b]是[a]的逆元.
[a][b] = [b][a] = [1]
[b]是[a]的负元.
则展开式的常数项为( )
针对性练习
2、设实数a≠0,{an}是以a为首项,-a为公比的等比数列,且bn=anlg|an|(nN),问当0
展开式的二项式系数之和为64,
1、
20
思考和分析 初看题目似乎很难下手,但只要我们冷静想一想,不妨假设存在m0 N,使对任意n N,都有bn bm0,也就是说bm0应该是数列{bn}的最大项,这样我们将问题化归为数列{bn}的最大项的存在性问题,从而就容易入手了.
3、???????????????????????????????????????????? 则A、B、C的关系是?
【解析】要判断集合A、B、C之间的关系,可以对每个集合中元素所满足的条件进行变形整理,然后找出条件式子结构的差异,最后只需比较这些“差异”就可以了.本试题中,
据整数剩余类知识知,3(n-1)+1(n∈Z)和3p+1都表示被3除余1的整数, 因而知B=C.又p∈Z,则令 知 ??????????
故 【点评】因为6m+1(m∈Z)表示被6除余1的整数,且为奇数;而3p+1(p∈Z)表示被
A ??B=C
3整除余1的整数,它可能是偶数,也可能是奇数,为了寻找集合A与C的关系,必须明确3p+1(p∈Z)何时为奇数以及奇数的类型,为此只需把p分类奇数和偶数即可.
辛苦~\(≧▽≦)/~啦啦啦
课堂练习
2、一个数被3除余2,被7除余4,被8除余5,这个数最小是( )
3、一个数除以5余4,除以8余3,除以11余2,满足条件的最小的自然数( ).
1、一年级同学,每9人一排多5人,每7人一排多1人,每5人一排多2人,至少有多少人( )
302
53
A.302 B.299 C.201 D.401
B
解:〔4,5〕=20;〔3,5〕=15;〔3,4〕=12;〔3,4,5〕=60.为了使20被3除余1,用20×2=40;使15被4除余1,用15×3=45;使12被5除余1,用12×3=36.然后,40×1+45×2+36×4=274,因为,274>60,所以,274-60×4=34,就是所求的数.
5、被3除余1,被4除余2,被5除余4,这个数最小是?
4、9人一排多6人,7人一排多2人,5人一排多3人,至少( )人 .
A.303 B.299 C.202 D.405
A
6、模m=10,根据余数可以将所有整数分成10个类别
[0]即 C0={c| c mod m=0 mod m}
={c| c mod 10=0 mod 10}
={c| c mod 10=0}={c|c=t?10}
={0,10,20,30,40,50,…,-10,-20,…}
[1]即 C1={c| c mod m=1 mod m}
={c| c mod m=1}={c| c=s?10+1}
={1,11,21,31,41,…,-11,-21,-31,…}
[a]即Ca={c| c mod m=a mod m} (a<10)
={c| c mod 10=a }
={c| c=k?10+a}
7、证明:不存在整数a、b、c,满足a2+b2-8c=6
证明 由于每个整数都具有下列形式之一4n,4n1,4n+2,
它们的平方数分别是:16n2,16n28n+1,16n2+16n+4,
它们被8除的余数分别是:0,1,4.而这三个余数的任意两数(可以相同)的和都不等于6,所以对任意整数a、b、c,a2+b2-8c=6.
再见
