人教版高中数学选修4-6 第二讲 同余与同余方程 三 费马小定理和欧拉定理 上课课件(共30张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第二讲 同余与同余方程 三 费马小定理和欧拉定理 上课课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:38:34 | ||
图片预览










文档简介
(共30张PPT)
知识回顾
剩余类定理
若a,b,c为任意3个整数,m为正整数,且(m,c)=1,则当ac≡bc(modm)时,有a≡b(modm)
如果a,b,c,d是四个整数,且a≡b(mod m),c≡d(mod m),则有ac≡bd(mod m).
同余定理
导入新课
上一讲我们讲了剩余类,剩余环并知道了它的运算法则.
剩余类乘法:[a][b]=[ɑb]
在整数集模6的剩余环中
[2][4]=[8]=[2]
[8][9]=[72]=[0]
[2][4][9]=[72]=[0]
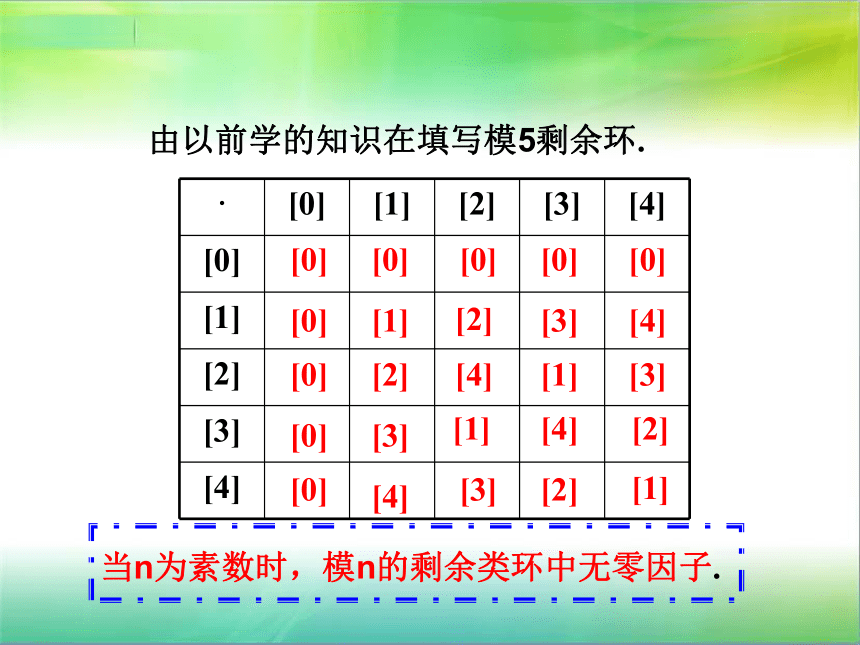
当n为素数时,模n的剩余类环中无零因子.
· [0] [1] [2] [3] [4]
[0]
[1]
[2]
[3]
[4]
由以前学的知识在填写模5剩余环.
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[1]
[2]
[3]
[4]
[2]
[3]
[4]
[4]
[1]
[3]
[1]
[3]
[4]
[2]
[2]
[1]
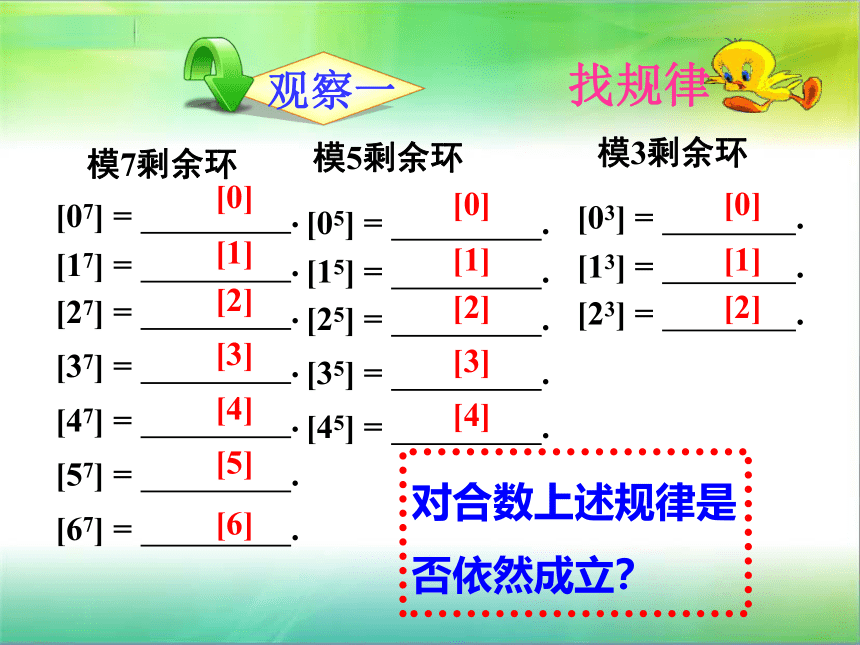
模7剩余环
[07] = .
[17] = .
[27] = .
[37] = .
[47] = .
[57] = .
[67] = .
[05] = .
[15] = .
[25] = .
[35] = .
[45] = .
[03] = .
[13] = .
[23] = .
模5剩余环
模3剩余环
[6]
[5]
[4]
[3]
[2]
[0]
[1]
[4]
[3]
[2]
[0]
[1]
[2]
[0]
[1]
对合数上述规律是否依然成立?
找规律
观察一
第三节 费马小定理和欧拉定理
第二讲 同余与同余方程
教学目标
知识与能力
1.理解费马小定理和欧拉定理的内容与证明过程.
2.能够运用费马小定理和欧拉定理简化数论中的一些计算问题.
情感态度与价值观
过程与方法
1.通过举例对比总结费马小定理和欧拉定理的定义.
2.由以前学过的知识,对费马小定理和欧拉定理进行证明.
认识费马小定理和欧拉定理的历史及地位和作用.
教学重难点
1.欧拉函数的定义及性质.
费马小定理和欧拉定理的证明过程,以及灵活运用这两个定理简化数论中的一些计算.
重点
难点
2.欧拉定理、Fermat小定理,循环小数的判定条件.
科普知识
瑞士著名的数学家欧拉,是数学史上的最多的数学家,他毕生从事数学研究,他的论著几乎涉及18世纪所以的数学分支.比如数学中的欧拉公式,欧拉方程.欧拉常数,欧拉方法.欧拉猜想等.欧拉晚年不幸双目失明,失明后的17年,他还口述署了几本书和约400篇论.
费马生于法国南部 ,贡献包括:与笛卡尔共同创立了解析几何;创造了作曲线切线的方法 .最有名的是费马大定理,即不可能有满足xn+yn=zn ,n>2的正整数x,y,z,n存在.费马小定理是费马在1640年提出.
科普知识
通过观察一,我们得到模7剩余环、模5剩余环、模3剩余环的规律,又由于3、5、7都是素数,我们猜想:
费马小定理 设m为素数,ɑ为任意整数,
实例
例一、若a=3,m=7,则am-1≡1(modm)成立否.
解:
有以前的知识我们知道
3×1 ≡3(mod7)
3×2 ≡6(mod7)
3×3 ≡2(mod7)
3×4 ≡5(mod7)
3×5 ≡1(mod7)
3×6 ≡4(mod7)
则:36×6!≡6!(mod7).(1)
又因为:(6!,5)=1 (2)
所以:36≡1(mod7)
即:am-1≡1(modm)
分析
在例一的解析中我们用到了以前学习的知识.
(1) 中用到了等式左边相乘等于等式右边相乘.
(2) 中用到了同余的性质“若ɑb ≡ɑc(modn),且(ɑ,n)=1,则b ≡c(modn)”.
例一的解析符合费马小定理,下面我们用通式对费马小定理给予证明.
设 An= a,2a,3a,4a…… (p-1)a 假设 An中有2项ma, na 被p除以后余数是相同 得 ma=na (mod p) 即a(m-n)=0(mod p) 因为 a和p互质, 所以 m-n=0(mod p) 又因为 m,n属于集合{1,2,3..p-1}且m不等于n 所以 m-n不可能是p的倍数. 推出 和假设产生矛盾.
证明
所以 An中任意2项被p除得到的余数都不同 又因为对于任一个整数被p除以后的余数最多有 p-1个,分别是1,2,3,….p-1 而数列An中恰好有p-1个数,所以数列中的数被p除以后的余数一定正好包含所有的1,2,3,4,5…. p-1 所以 a*2a*3a*…(p-1)a=1*2*3*4…*(p-1) (mod p)对两边进行化简,即可以得到a(p-1)=1 (mod p)
巩固
1、11x≡1(mod3),则x=( ).
2、114≡1(modx),则x=( ).
3、116≡x(mod7),则x=( ).
4、x6≡1(mod7),1-10之内x可能为( ).
5
2
1、2、3、4、5、6、8、9、10
1
我们看到在费马小定理中针对的是m为素数的情况,对于其它数能否找到类似的性质呢,这就是下面要讲的欧拉定理.
拓展
欧拉定理 设m为正整数,ɑ为任意整数,且(ɑ, m )=1,则
( 1 ) 令
则 Zn = S .
① 因为 a 与 n 互质, xi (1 ≤ i ≤ φ(n)) 与 n 互质, 所以 a * xi 与 n 互质,所以 a * xi mod n ∈ Zn .
② 若 i ≠ j , 那么 xi ≠ xj,且由 a, n互质可得 a * xi mod n ≠ a * xj mod n (消去律).
证明:
对比等式的左右两端,因为 xi (1 ≤ i ≤ φ(n)) 与 n 互质,所以 aφ(n) ≡ 1 mod n (消去律).
(2)
课堂小结
1、费马小定理
设m为素数, a为任意整数,且(a,m)
2、欧拉定理
设m为正整数,ɑ为任意整数,且(ɑ,m )=1,则 其中?(m) 表示1,2,…, m中与m互素的正整数的个数.
针对性练习
一、 设a,b,c,m是正整数,m > 1, (b, m) = 1, 并且b a ? 1 (mod m),b c ? 1 (mod m), 记d = (a, c),则bd ? 1 (mod m).
解 利用辗转相除法可以求出整数x,y,使得ax ? cy = d,显然xy < 0.
若 x > 0,y < 0,由式(4)知
1 ? b ax = b db ?cy = b d(b c) ?y ? b d (mod m)。
若 x < 0,y > 0,由式(4)知
1 ? b cy = b db ?ax = b d(ba) ?x ? b d (mod m)。
二、设p是素数,p?bn ? 1,n?N,则下面的两个结论中至少有一个成立: (ⅰ) p?bd ? 1对于n的某个因数d < n成立; (ⅱ) p ? 1 ( mod n ).
p > 2,则(ⅱ)中的mod n可以改为mod 2n.
解 记d = (n, p ? 1),由b n ? 1,b p ? 1 ? 1 (mod p),及题一,有b d ? 1 (mod p).
若d < n,则结论(ⅰ)得证.
若d = n,则n?p ? 1,即p ? 1 (mod n),这就是结论(ⅱ).
p > 2,则p ?1 (mod 2). 由此及结论(ⅱ),并利用同余的基本性质,得到 p ? 1 (mod 2n).
这是一种解题方法好好掌握吆.
解 由题二知
若 p?235 ? 1
则 p是25 ? 1 = 31或27 ? 1 = 127的素因数
或者 p ? 1 (mod 70)
由于 31和127是素数
并且 235 ? 1 = 31*127*8727391
所以,235 ? 1的另外的素因数p只可能在数列
三、 将235 ? 1 = 34359738367分解因数.
71,211,281,? (5) 中
经检验,得到8727391 = 71*122921.
显然,122921的素因数在31,127或者数列(5)中
说明,122921不能被31和127整除,也不能被数
列(5)中的不超过
的数整除,所以122921是素数
于是 235 ? 1 = 31*127*71*122921.
课堂练习
1、313159被7除的余数 ( ).
6 (mod 7)
2、132005被17除的余数 ( ).
13 (mod 17)
3、17x≡1(mod5),则x=( ).
A.5 B.6 C.4 D.7
C
4、5x≡1(mod6),则x=( ).
A.5 B.6 C.4 D.2
D
5、设p,q是两个不同的素数,证明:
pq ? 1 ? qp ? 1 ? 1 (mod pq).
由费马定理:
qp ? 1 ? 1 (mod p), pq ? 1 ? 1 (mod q)
pq ? 1 ? qp ? 1 ? 1 (mod p)
pq ? 1 ? qp ? 1 ? 1 (mod q)
故 pq ? 1 ? qp ? 1 ? 1 (mod pq).
证明:
612 ? 1 = (63 ? 1)( 63 ? 1)( 66 ? 1)
=5*43*7*31*46657 对于46657,它的素因数必为12k ? 1型, 经检验的46657 = 13*37*97 故612 ? 1 = 5*7*13*31*37*43*97.
6、将612 ? 1分解成素因数之积.
解:
证明:因561 = 3*11*17,对于一切整数a,(a, 561) = 1,有(a, 3) = 1,(a, 11) = 1,(a, 17) = 1, 由费马定理可得a560 = (a2)280 ? 1 (mod 3),a560 = (a10)56 ? 1 (mod 11),a560 = (a16)35 ? 1 (mod 17),故a560 ? 1 (mod 561).
7、证明:对于任意的整数a,(a, 561) = 1,都有a560 ? 1 (mod 561),但561是合数.
再见
知识回顾
剩余类定理
若a,b,c为任意3个整数,m为正整数,且(m,c)=1,则当ac≡bc(modm)时,有a≡b(modm)
如果a,b,c,d是四个整数,且a≡b(mod m),c≡d(mod m),则有ac≡bd(mod m).
同余定理
导入新课
上一讲我们讲了剩余类,剩余环并知道了它的运算法则.
剩余类乘法:[a][b]=[ɑb]
在整数集模6的剩余环中
[2][4]=[8]=[2]
[8][9]=[72]=[0]
[2][4][9]=[72]=[0]
当n为素数时,模n的剩余类环中无零因子.
· [0] [1] [2] [3] [4]
[0]
[1]
[2]
[3]
[4]
由以前学的知识在填写模5剩余环.
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[0]
[1]
[2]
[3]
[4]
[2]
[3]
[4]
[4]
[1]
[3]
[1]
[3]
[4]
[2]
[2]
[1]
模7剩余环
[07] = .
[17] = .
[27] = .
[37] = .
[47] = .
[57] = .
[67] = .
[05] = .
[15] = .
[25] = .
[35] = .
[45] = .
[03] = .
[13] = .
[23] = .
模5剩余环
模3剩余环
[6]
[5]
[4]
[3]
[2]
[0]
[1]
[4]
[3]
[2]
[0]
[1]
[2]
[0]
[1]
对合数上述规律是否依然成立?
找规律
观察一
第三节 费马小定理和欧拉定理
第二讲 同余与同余方程
教学目标
知识与能力
1.理解费马小定理和欧拉定理的内容与证明过程.
2.能够运用费马小定理和欧拉定理简化数论中的一些计算问题.
情感态度与价值观
过程与方法
1.通过举例对比总结费马小定理和欧拉定理的定义.
2.由以前学过的知识,对费马小定理和欧拉定理进行证明.
认识费马小定理和欧拉定理的历史及地位和作用.
教学重难点
1.欧拉函数的定义及性质.
费马小定理和欧拉定理的证明过程,以及灵活运用这两个定理简化数论中的一些计算.
重点
难点
2.欧拉定理、Fermat小定理,循环小数的判定条件.
科普知识
瑞士著名的数学家欧拉,是数学史上的最多的数学家,他毕生从事数学研究,他的论著几乎涉及18世纪所以的数学分支.比如数学中的欧拉公式,欧拉方程.欧拉常数,欧拉方法.欧拉猜想等.欧拉晚年不幸双目失明,失明后的17年,他还口述署了几本书和约400篇论.
费马生于法国南部 ,贡献包括:与笛卡尔共同创立了解析几何;创造了作曲线切线的方法 .最有名的是费马大定理,即不可能有满足xn+yn=zn ,n>2的正整数x,y,z,n存在.费马小定理是费马在1640年提出.
科普知识
通过观察一,我们得到模7剩余环、模5剩余环、模3剩余环的规律,又由于3、5、7都是素数,我们猜想:
费马小定理 设m为素数,ɑ为任意整数,
实例
例一、若a=3,m=7,则am-1≡1(modm)成立否.
解:
有以前的知识我们知道
3×1 ≡3(mod7)
3×2 ≡6(mod7)
3×3 ≡2(mod7)
3×4 ≡5(mod7)
3×5 ≡1(mod7)
3×6 ≡4(mod7)
则:36×6!≡6!(mod7).(1)
又因为:(6!,5)=1 (2)
所以:36≡1(mod7)
即:am-1≡1(modm)
分析
在例一的解析中我们用到了以前学习的知识.
(1) 中用到了等式左边相乘等于等式右边相乘.
(2) 中用到了同余的性质“若ɑb ≡ɑc(modn),且(ɑ,n)=1,则b ≡c(modn)”.
例一的解析符合费马小定理,下面我们用通式对费马小定理给予证明.
设 An= a,2a,3a,4a…… (p-1)a 假设 An中有2项ma, na 被p除以后余数是相同 得 ma=na (mod p) 即a(m-n)=0(mod p) 因为 a和p互质, 所以 m-n=0(mod p) 又因为 m,n属于集合{1,2,3..p-1}且m不等于n 所以 m-n不可能是p的倍数. 推出 和假设产生矛盾.
证明
所以 An中任意2项被p除得到的余数都不同 又因为对于任一个整数被p除以后的余数最多有 p-1个,分别是1,2,3,….p-1 而数列An中恰好有p-1个数,所以数列中的数被p除以后的余数一定正好包含所有的1,2,3,4,5…. p-1 所以 a*2a*3a*…(p-1)a=1*2*3*4…*(p-1) (mod p)对两边进行化简,即可以得到a(p-1)=1 (mod p)
巩固
1、11x≡1(mod3),则x=( ).
2、114≡1(modx),则x=( ).
3、116≡x(mod7),则x=( ).
4、x6≡1(mod7),1-10之内x可能为( ).
5
2
1、2、3、4、5、6、8、9、10
1
我们看到在费马小定理中针对的是m为素数的情况,对于其它数能否找到类似的性质呢,这就是下面要讲的欧拉定理.
拓展
欧拉定理 设m为正整数,ɑ为任意整数,且(ɑ, m )=1,则
( 1 ) 令
则 Zn = S .
① 因为 a 与 n 互质, xi (1 ≤ i ≤ φ(n)) 与 n 互质, 所以 a * xi 与 n 互质,所以 a * xi mod n ∈ Zn .
② 若 i ≠ j , 那么 xi ≠ xj,且由 a, n互质可得 a * xi mod n ≠ a * xj mod n (消去律).
证明:
对比等式的左右两端,因为 xi (1 ≤ i ≤ φ(n)) 与 n 互质,所以 aφ(n) ≡ 1 mod n (消去律).
(2)
课堂小结
1、费马小定理
设m为素数, a为任意整数,且(a,m)
2、欧拉定理
设m为正整数,ɑ为任意整数,且(ɑ,m )=1,则 其中?(m) 表示1,2,…, m中与m互素的正整数的个数.
针对性练习
一、 设a,b,c,m是正整数,m > 1, (b, m) = 1, 并且b a ? 1 (mod m),b c ? 1 (mod m), 记d = (a, c),则bd ? 1 (mod m).
解 利用辗转相除法可以求出整数x,y,使得ax ? cy = d,显然xy < 0.
若 x > 0,y < 0,由式(4)知
1 ? b ax = b db ?cy = b d(b c) ?y ? b d (mod m)。
若 x < 0,y > 0,由式(4)知
1 ? b cy = b db ?ax = b d(ba) ?x ? b d (mod m)。
二、设p是素数,p?bn ? 1,n?N,则下面的两个结论中至少有一个成立: (ⅰ) p?bd ? 1对于n的某个因数d < n成立; (ⅱ) p ? 1 ( mod n ).
p > 2,则(ⅱ)中的mod n可以改为mod 2n.
解 记d = (n, p ? 1),由b n ? 1,b p ? 1 ? 1 (mod p),及题一,有b d ? 1 (mod p).
若d < n,则结论(ⅰ)得证.
若d = n,则n?p ? 1,即p ? 1 (mod n),这就是结论(ⅱ).
p > 2,则p ?1 (mod 2). 由此及结论(ⅱ),并利用同余的基本性质,得到 p ? 1 (mod 2n).
这是一种解题方法好好掌握吆.
解 由题二知
若 p?235 ? 1
则 p是25 ? 1 = 31或27 ? 1 = 127的素因数
或者 p ? 1 (mod 70)
由于 31和127是素数
并且 235 ? 1 = 31*127*8727391
所以,235 ? 1的另外的素因数p只可能在数列
三、 将235 ? 1 = 34359738367分解因数.
71,211,281,? (5) 中
经检验,得到8727391 = 71*122921.
显然,122921的素因数在31,127或者数列(5)中
说明,122921不能被31和127整除,也不能被数
列(5)中的不超过
的数整除,所以122921是素数
于是 235 ? 1 = 31*127*71*122921.
课堂练习
1、313159被7除的余数 ( ).
6 (mod 7)
2、132005被17除的余数 ( ).
13 (mod 17)
3、17x≡1(mod5),则x=( ).
A.5 B.6 C.4 D.7
C
4、5x≡1(mod6),则x=( ).
A.5 B.6 C.4 D.2
D
5、设p,q是两个不同的素数,证明:
pq ? 1 ? qp ? 1 ? 1 (mod pq).
由费马定理:
qp ? 1 ? 1 (mod p), pq ? 1 ? 1 (mod q)
pq ? 1 ? qp ? 1 ? 1 (mod p)
pq ? 1 ? qp ? 1 ? 1 (mod q)
故 pq ? 1 ? qp ? 1 ? 1 (mod pq).
证明:
612 ? 1 = (63 ? 1)( 63 ? 1)( 66 ? 1)
=5*43*7*31*46657 对于46657,它的素因数必为12k ? 1型, 经检验的46657 = 13*37*97 故612 ? 1 = 5*7*13*31*37*43*97.
6、将612 ? 1分解成素因数之积.
解:
证明:因561 = 3*11*17,对于一切整数a,(a, 561) = 1,有(a, 3) = 1,(a, 11) = 1,(a, 17) = 1, 由费马定理可得a560 = (a2)280 ? 1 (mod 3),a560 = (a10)56 ? 1 (mod 11),a560 = (a16)35 ? 1 (mod 17),故a560 ? 1 (mod 561).
7、证明:对于任意的整数a,(a, 561) = 1,都有a560 ? 1 (mod 561),但561是合数.
再见
