人教版高中数学选修4-6 第二讲 同余与同余方程 五 拉格朗日插值和孙子定理 上课课件(共27张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第二讲 同余与同余方程 五 拉格朗日插值和孙子定理 上课课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:48:34 | ||
图片预览








文档简介
(共27张PPT)
知识回顾
学过的函数:
一次函数 f(x)=ax+b+c
二次函数 f(x)=ax2+bx+c
f(1)= a+b+c
f(-1)= a-b+c
f(2)= 4a+2b+c
方程组:
导入新课
今有物不知数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
你能算出来吗?
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何? 这四句话的意思是:有若干 只鸡兔同在一个笼子里,从 上面数,有35个头;从下面 数,有94只脚.求笼中各有几只鸡和兔 .
你知道有多少只鸡吗?
你能够解决以上的问题,求出数值吗?要解决以上的问题穷举法显然是不可能的,这就涉及到我们今天要学习的知识,拉格朗日插值法、孙子定理.
第五节 拉格朗日插值和孙子定理
第二讲 同余与同余方程
教学目标
知识与能力
1.理解一次同余式组的概念. 2.理解拉格朗日插值公式的建立过程及推导孙子定理的过程.
3.掌握用孙子定理法求一次同余式组的解.
过程与方法
情感态度与价值观
1.通过算法案例的学习,了解中国古代数学家对世界数学发展的伟大贡献,增强民自豪感和自信心. 2.在学习的同时,学会做有爱国心,品格高尚的人,树立远大理想和目标.
1.先阅读案例,探究解决问题的算法.
2.研读算法,体会算法思想,能解决具体问题.
教学重难点
重点
1.理解拉格朗日插值公式的建立过程. 2.孙子定理的推导过程. 3.用孙子定理解一次同余方程.
难点
建立拉格朗日插值公式和推导孙子定理.
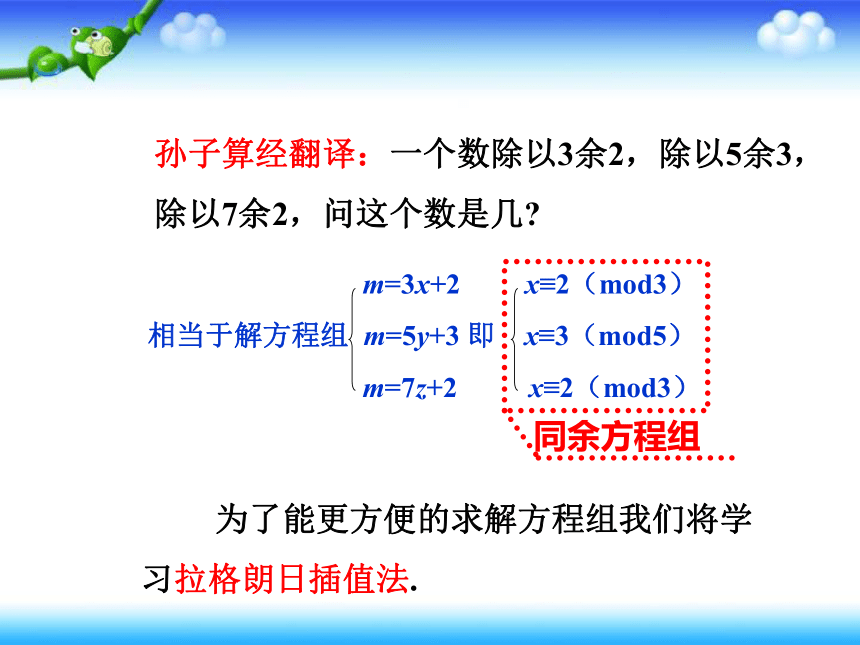
孙子算经翻译:一个数除以3余2,除以5余3,除以7余2,问这个数是几?
m=3x+2 x≡2(mod3)
相当于解方程组 m=5y+3 即 x≡3(mod5)
m=7z+2 x≡2(mod3)
同余方程组
为了能更方便的求解方程组我们将学习拉格朗日插值法.
我们知道,在二次函数f(x)=ax2+bx+c中只要我们知道其上的三个值如(x1,f(x1)), (x2,f(x2)), (x2,f(x2)),就能得到要求的多项事.一种更一般的拉格朗日插值法. 1)求多项式p(x),使p(x1)=1,p(x2)=0,p(x3)=0 2)求多项式q(x),使q(x1)=0,q(x2)=1,q(x3)=0 3)求多项式r(x),使r(x1)=0,r(x2)=0,r(x3)=1 若选取p(x)=c(x-x2)(x-x3),其中c为常数.
显然p(x2)=0,p(x3)=0 再代入p(x1)=1,可求得c为 (x1 - x2)( x1 – x3)的倒数. 求得
同理得
设a,b,c两两不同那么满足f(a)=e,f(b)=f , f(c)=g的一个多项式可用
f(x)=e· p(x)+f · q(x)+ g · r(x) (Ⅰ) 其中 (Ⅱ)
上面的公式(Ⅰ)和(Ⅱ)叫做拉格朗日公式.用类似方法解决孙子算经的物不知其数问题. 1)求整数p,使p≡1(mod3), p ≡0(mod5), p≡0(mod7).
求整数q,使q≡0(mod3), q ≡1(mod5), q≡0(mod7).
求整数r,使r≡0(mod3), r ≡0(mod5), r≡1(mod7).
2)作整数k=2×p+3×q+2×r,这个k使同余式都成了.此时x≡k(mod3×5×7)现在的焦点就是如何求p、q、r. 由于p≡0(mod5),p ≡1(mod7) 故 5︱p,7︱p,于是p=5×7×c,c为整数再由p≡1(mod3)即5×7×c ≡1(mod3) 若c=2,则p=70.同理求得q=21,r=15. 所以k=233,x ≡233≡23(mod105).
此求同余方程组的方法即孙子定理.
孙子定理 设a,b,c为两两互素的正整数,e,f,g为任意整数,则同余方程组
x≡e(moda),
x≡f(modb),仅有一解:
x≡g(modc) x≡ebcc1+facc2+gabc3(modabc),其中c1,c2,c3分别满足同余式:bcc1≡1(moda) acc2 ≡1(modb),abc3 ≡1(moda)的整数.
课堂小结
一、一次同余式组:
x≡e(moda)
x≡f(modb)
x≡g(modc)
二、拉格朗日插值公式:
f(x)=e· p(x)+f · q(x)+ g · r(x)
三、孙子定理:
设a,b,c为两两互素的正整数,e,f,g为任意整数,则同余方程组
x≡e(moda)
x≡f(modb),仅有一解:
x≡g(modc) x≡ebcc1+facc2+gabc3(modabc),其中c1,c2,c3分别满足同余式:bcc1≡1(moda) acc2 ≡1(modb),abc3 ≡1(moda)的整数.
针对性练习
1、已知函数f(x)=x2+2x+alnx当t≥1时, 不等式f(2t-1) ≥2f(t)-3恒成立, 求实数a的取值范围.
证明:当t≥1时,f(2t-1)≥2f(t)-3 恒成立. 即(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3当t≥1恒成立. 即a[lnt2-ln(2t-1)] ≤2(t-1)2
h(x)=lnx,由拉格朗日定理知, 使得 成立 故 所以 即实数取值范围(-∞,2]
当t=1时,不等式恒成立,此时a∈R. 当t>1时,由于t2-(2t-1)=(t-1)2>0, 所以 lnt2>ln(2t-1) 故 当t≥1时恒成立.
2、已知函数 , f(x)的导数是f’(x),任意两个不等正数x1,x2证:若a≤4,︳ f’(x1)- f’(x2) ︳> ︱x1- x2 ︳ ,
证明:要证︱f’(x1)- f’(x2) ︳> ︱x1- x2 ︳ 只要证 由拉格朗日定理,总存在
使 故只要证明 只要证
令 ,则 令 故当a≤4时︱f’(x1)- f’(x2) ︳> ︱x1- x2 ︳
3、已知函数 且存在x0∈(0, ) ,使f(x0)=x0. 证明:
证明: 因为 由拉格朗日中值定理知: 总存在 使得
由于 又
当 故得证
1、求整数n,它被3,5,7除的余数分别是1,2,3,则该整数最小为( ).
2、解同余方程组
则x为( ).
课堂练习
52
21531056
4、一个数被3除余1,被4除余2,被5除余4,这个数最小是( ).
3、有一个数,除以3余2,除以4余1,问这个数除以12余( ).
A.5 B. 7 C.8 D.9
A
A.274 B. 40 C.34 D.36
C
解析:若4人一组多1人,6人一组少3人,则加3人为4和6的公约数=12K,12K-3能被5整除,根据5和2的倍数特征规律:12×4-3=45,所以至少有45人.
5、若4人一组多1人,5人一组正好分完,6人一组少3人,最少有几人?
6、每9人一排多6人,每7人一排多2人,每5人一排多3人,问至少有多少人 ?
解:由于9,7,5互素,故同样可用孙子定理.
解1 7×5c1 =35c1≡1(mod9) 得 c1 ≡ 8(mod9),
解2 9×5c2 =45c2≡1(mod7) 得 c2 ≡ 5(mod7),
解3 9×7c3 =63c3≡1(mod5) 得 c3 ≡ 2(mod5),
于是,选取c1=2, c2=3, c3=11 得x≡6×7×5×8+2×9×5×5+3×9×7×2 ≡303(mod305) 是同余方程的解.所以至少303人.
解:由于3,7,11互素,故同样可用孙子定理.
解1 7×11c1 =77c1≡1(mod3) 得 c1 ≡ 2(mod2),
解2 3×11c2 =33c2≡1(mod7) 得 c2 ≡ 3(mod7), 解3 3×7c3 =21c3≡1(mod11) 得 c3 ≡ 10(mod11),
于是,选取c1=2, c2=3, c3=11 得x≡2×7×11×2+1×3×11×3+2×3×7×10=727
≡24(mod231) 是同余方程的解.
7、3除余2,被7除余1,被11除余2,求同余方程的解.
再见
知识回顾
学过的函数:
一次函数 f(x)=ax+b+c
二次函数 f(x)=ax2+bx+c
f(1)= a+b+c
f(-1)= a-b+c
f(2)= 4a+2b+c
方程组:
导入新课
今有物不知数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?
你能算出来吗?
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何? 这四句话的意思是:有若干 只鸡兔同在一个笼子里,从 上面数,有35个头;从下面 数,有94只脚.求笼中各有几只鸡和兔 .
你知道有多少只鸡吗?
你能够解决以上的问题,求出数值吗?要解决以上的问题穷举法显然是不可能的,这就涉及到我们今天要学习的知识,拉格朗日插值法、孙子定理.
第五节 拉格朗日插值和孙子定理
第二讲 同余与同余方程
教学目标
知识与能力
1.理解一次同余式组的概念. 2.理解拉格朗日插值公式的建立过程及推导孙子定理的过程.
3.掌握用孙子定理法求一次同余式组的解.
过程与方法
情感态度与价值观
1.通过算法案例的学习,了解中国古代数学家对世界数学发展的伟大贡献,增强民自豪感和自信心. 2.在学习的同时,学会做有爱国心,品格高尚的人,树立远大理想和目标.
1.先阅读案例,探究解决问题的算法.
2.研读算法,体会算法思想,能解决具体问题.
教学重难点
重点
1.理解拉格朗日插值公式的建立过程. 2.孙子定理的推导过程. 3.用孙子定理解一次同余方程.
难点
建立拉格朗日插值公式和推导孙子定理.
孙子算经翻译:一个数除以3余2,除以5余3,除以7余2,问这个数是几?
m=3x+2 x≡2(mod3)
相当于解方程组 m=5y+3 即 x≡3(mod5)
m=7z+2 x≡2(mod3)
同余方程组
为了能更方便的求解方程组我们将学习拉格朗日插值法.
我们知道,在二次函数f(x)=ax2+bx+c中只要我们知道其上的三个值如(x1,f(x1)), (x2,f(x2)), (x2,f(x2)),就能得到要求的多项事.一种更一般的拉格朗日插值法. 1)求多项式p(x),使p(x1)=1,p(x2)=0,p(x3)=0 2)求多项式q(x),使q(x1)=0,q(x2)=1,q(x3)=0 3)求多项式r(x),使r(x1)=0,r(x2)=0,r(x3)=1 若选取p(x)=c(x-x2)(x-x3),其中c为常数.
显然p(x2)=0,p(x3)=0 再代入p(x1)=1,可求得c为 (x1 - x2)( x1 – x3)的倒数. 求得
同理得
设a,b,c两两不同那么满足f(a)=e,f(b)=f , f(c)=g的一个多项式可用
f(x)=e· p(x)+f · q(x)+ g · r(x) (Ⅰ) 其中 (Ⅱ)
上面的公式(Ⅰ)和(Ⅱ)叫做拉格朗日公式.用类似方法解决孙子算经的物不知其数问题. 1)求整数p,使p≡1(mod3), p ≡0(mod5), p≡0(mod7).
求整数q,使q≡0(mod3), q ≡1(mod5), q≡0(mod7).
求整数r,使r≡0(mod3), r ≡0(mod5), r≡1(mod7).
2)作整数k=2×p+3×q+2×r,这个k使同余式都成了.此时x≡k(mod3×5×7)现在的焦点就是如何求p、q、r. 由于p≡0(mod5),p ≡1(mod7) 故 5︱p,7︱p,于是p=5×7×c,c为整数再由p≡1(mod3)即5×7×c ≡1(mod3) 若c=2,则p=70.同理求得q=21,r=15. 所以k=233,x ≡233≡23(mod105).
此求同余方程组的方法即孙子定理.
孙子定理 设a,b,c为两两互素的正整数,e,f,g为任意整数,则同余方程组
x≡e(moda),
x≡f(modb),仅有一解:
x≡g(modc) x≡ebcc1+facc2+gabc3(modabc),其中c1,c2,c3分别满足同余式:bcc1≡1(moda) acc2 ≡1(modb),abc3 ≡1(moda)的整数.
课堂小结
一、一次同余式组:
x≡e(moda)
x≡f(modb)
x≡g(modc)
二、拉格朗日插值公式:
f(x)=e· p(x)+f · q(x)+ g · r(x)
三、孙子定理:
设a,b,c为两两互素的正整数,e,f,g为任意整数,则同余方程组
x≡e(moda)
x≡f(modb),仅有一解:
x≡g(modc) x≡ebcc1+facc2+gabc3(modabc),其中c1,c2,c3分别满足同余式:bcc1≡1(moda) acc2 ≡1(modb),abc3 ≡1(moda)的整数.
针对性练习
1、已知函数f(x)=x2+2x+alnx当t≥1时, 不等式f(2t-1) ≥2f(t)-3恒成立, 求实数a的取值范围.
证明:当t≥1时,f(2t-1)≥2f(t)-3 恒成立. 即(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3当t≥1恒成立. 即a[lnt2-ln(2t-1)] ≤2(t-1)2
h(x)=lnx,由拉格朗日定理知, 使得 成立 故 所以 即实数取值范围(-∞,2]
当t=1时,不等式恒成立,此时a∈R. 当t>1时,由于t2-(2t-1)=(t-1)2>0, 所以 lnt2>ln(2t-1) 故 当t≥1时恒成立.
2、已知函数 , f(x)的导数是f’(x),任意两个不等正数x1,x2证:若a≤4,︳ f’(x1)- f’(x2) ︳> ︱x1- x2 ︳ ,
证明:要证︱f’(x1)- f’(x2) ︳> ︱x1- x2 ︳ 只要证 由拉格朗日定理,总存在
使 故只要证明 只要证
令 ,则 令 故当a≤4时︱f’(x1)- f’(x2) ︳> ︱x1- x2 ︳
3、已知函数 且存在x0∈(0, ) ,使f(x0)=x0. 证明:
证明: 因为 由拉格朗日中值定理知: 总存在 使得
由于 又
当 故得证
1、求整数n,它被3,5,7除的余数分别是1,2,3,则该整数最小为( ).
2、解同余方程组
则x为( ).
课堂练习
52
21531056
4、一个数被3除余1,被4除余2,被5除余4,这个数最小是( ).
3、有一个数,除以3余2,除以4余1,问这个数除以12余( ).
A.5 B. 7 C.8 D.9
A
A.274 B. 40 C.34 D.36
C
解析:若4人一组多1人,6人一组少3人,则加3人为4和6的公约数=12K,12K-3能被5整除,根据5和2的倍数特征规律:12×4-3=45,所以至少有45人.
5、若4人一组多1人,5人一组正好分完,6人一组少3人,最少有几人?
6、每9人一排多6人,每7人一排多2人,每5人一排多3人,问至少有多少人 ?
解:由于9,7,5互素,故同样可用孙子定理.
解1 7×5c1 =35c1≡1(mod9) 得 c1 ≡ 8(mod9),
解2 9×5c2 =45c2≡1(mod7) 得 c2 ≡ 5(mod7),
解3 9×7c3 =63c3≡1(mod5) 得 c3 ≡ 2(mod5),
于是,选取c1=2, c2=3, c3=11 得x≡6×7×5×8+2×9×5×5+3×9×7×2 ≡303(mod305) 是同余方程的解.所以至少303人.
解:由于3,7,11互素,故同样可用孙子定理.
解1 7×11c1 =77c1≡1(mod3) 得 c1 ≡ 2(mod2),
解2 3×11c2 =33c2≡1(mod7) 得 c2 ≡ 3(mod7), 解3 3×7c3 =21c3≡1(mod11) 得 c3 ≡ 10(mod11),
于是,选取c1=2, c2=3, c3=11 得x≡2×7×11×2+1×3×11×3+2×3×7×10=727
≡24(mod231) 是同余方程的解.
7、3除余2,被7除余1,被11除余2,求同余方程的解.
再见
