人教版高中数学选修4-6 第二讲 同余与同余方程(一)同余 上课课件(共30张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第二讲 同余与同余方程(一)同余 上课课件(共30张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:48:00 | ||
图片预览












文档简介
(共30张PPT)
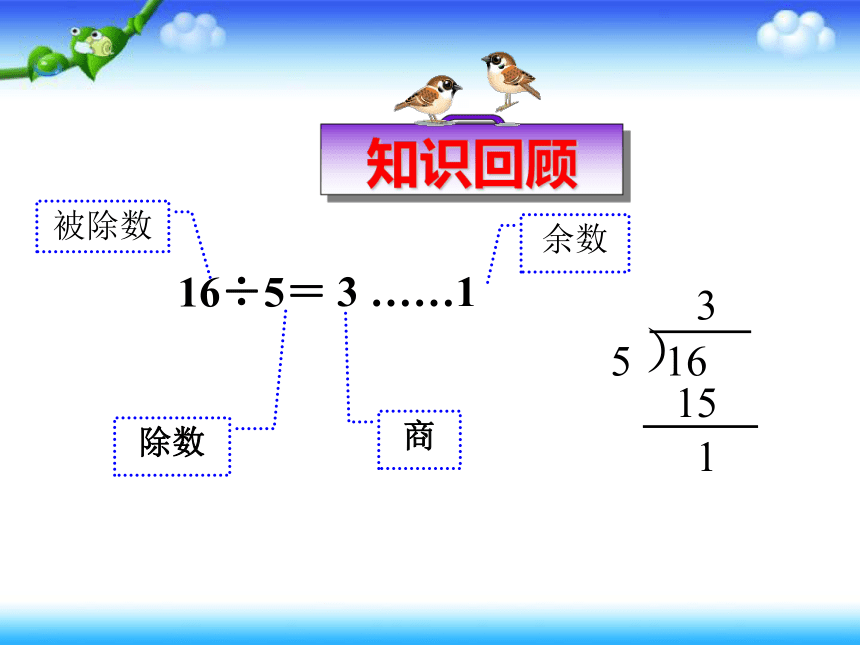
知识回顾
16÷5=
5 16
)
3
15
1
3 ……1
除数
商
余数
被除数
导入新课
今天是星期日,再过15天就是“六·一”儿童节了,问“六·一”儿童节是星期几?
因为,一个星期有7天,而15÷7=2…1,即15=7×2+1,所以“六·一”儿童节是星期一.
解析:
2020年的元旦是星期三,2021年的元旦是星期几?
因为,2020年有366天,而366=7×52+2,所以,2021年的元旦应该是星期五.
解析:
下一节我们将学习利用余数来解决生活中的问题.
以上问题的实质是求用7去除以总的天数后所得的余数.在日常生活中,时常要注意两个整数用某一固定的自然数去除,所得的余数问题.
第二讲 同余与同余方程
第一节 同余
教学目标
知识与能力
1.理解同余概念与整除概念的联系,掌握同余的性质及应用.
2.并能灵活应用同余的基本性质解决具体问题.
3.灵活运用同余的性质解决现实生活中的实际问题.
过程与方法
情感态度与价值观
2.观察同余与整数之间的关系,并通过实例深化理解.
1.通过举例,引出同余的概念和记号.
培养学生结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
教学重难点
重 点
1.准确理解同余的概念,正确的使用同余的符号.
难 点
2.类比等式的性质,探究证明同余的一些重要性质.
灵活运用同余的性质解决生活、理论中的实际问题.
12÷5=2…2
17÷5=3…2
22÷5=4…2
27÷5=5…2
32÷5=6…2
37÷5=7…2
……
被除数 除数 商 余数
12 5 2 2
17 5 3 2
22 5 4 2
27 5 5 2
32 5 6 2
37 5 7 2
… 5 … 2
观察上表有什么规律
通过观察,我们发现这些数被5整除后,得到的余数是相同的,这种情况我们成为模7同余.
一般地,设n为正整数,a和b为整数.如果a和b被n除后余数相同,那么称a和b模n同余,记作a ? b (mod n) .若a和b被n除后余数不同,则称a和b模n不同余,记作a b (mod n)
1)26和-14同时被4除判断他们的同余性,并用符号表示. 2)-14和22同时被4除判断他们的同余性,并用符号表示. 3)26和22同时被4除判断他们的同余性,并用符号表示. 4)26减去-14能否被4整除?
26÷4=4…2,
解析:
1)
-14÷4=-3…2
由定义知26和-14同余,故可写成
26 ? -14 (mod 4)
-14÷4=-3…2,
2)
22÷4=5…2
由定义知-14和22同余,故可写成
-14 ? 22 (mod 4)
-14 ? -26 (mod 4)
或
22 ? -14 (mod 4)
或
26÷4=4…2,
3)
22÷4=5…2
由定义知26和4同余,故可写成
26 ? 22 (mod 4)
26 ? 22 (mod 4)
或
解析:
4)
26-(-14) =40
4︱40
总结:
我们假设在上例中的a=26,b=-14,c=22,n=4.
-14 ? 22 (mod 4)
26 ? 22 (mod 4)
表示为:
1)
26 ? -14 (mod 4)
a ? b (mod n)
b ? c (mod n)
2)
3)
a ? c (mod n)
或
b ? a (mod n)
或
c ? b (mod n)
或
c ? a (mod n)
由以上实例可以总结出如下性质:
①自反性: a?a (mod n).
②对称性: 若a?b(mod n), 则b?a(mod n).
③传递性: 若a?b(mod n), b?c(mod n),
则: a?c(mod n).
④与整数的关系: a?b(mod n)
总结:
n︱a-b
若a?b(mod m), c?d(mod m), 则:
① ax+cy ? bx+dy(mod m), 其中x和y为任给整数.
② ac ? bd(mod m).
③ an ? bn(mod m), 其中 n>0.
④ f(a) ?f(b)(mod m), f(x)为任给的整系数多项式.
⑤ xa ?xb(mod m),x为任意整数.
探究
1、
若ab?ac(mod m), 且(a,n)=1,则b?c(mod m)
2、
性质应用
试求,17是否可以整除191000,若可以整除商是多少?余数是多少?
解:
因为
19 ? 2 (mod 17),
所以
191000 ? 21000 (mod 17) = 16250 (mod 17)
又因为
16 ? -1 (mod 17),
所以
16250 ? (- 1)250 (mod 17),
所以
17不能整除191000 ,余数为1
总结
在遇到很大的数时,我们很难直观判断余数是几,这时我们就要把被除数变小,降次,反复进行这个过程,直至求出结果.
如被除数为Ab (假设 Ab是一个很大的数),除数为C, 若C除以A余数为D,则Ab? Db (mod C) ;反复进行此过程直到求出结果.
课堂小结
同余定义
一般地,设n为正整数,a和b为整数.如果a和b被n除后余数相同,那么称a和b模n同余,记作a ? b (mod n) .若a和b被n除后余数不同,则称a和b模n不同余,记作a b (mod n)
由以上实例可以总结出如下性质:
①自反性: a?a (mod n).
②对称性: 若a?b(mod n), 则b?a(mod n).
③传递性: 若a?b(mod n), b?c(mod n),
则: a?c(mod n).
④与整数的关系: a?b(mod n)
n︱a-b
同余性质
若a?b(mod m), c?d(mod m), 则:
① ax+cy ? bx+dy(mod m), 其中x和y为任给整数.
② ac ? bd(mod m).
③ an ? bn(mod m), 其中 n>0.
④ f(a) ?f(b)(mod m), f(x)为任给的整系数多项式.
⑤ xa ?xb(mod m),x为任意整数.
1、
若ab?ac(mod m), 且(a,n)=1,则b?c(mod m)
2、
b≡a(mod 10),那么b的可能值是( )
针对性练习
1、设a、b、n(n>0)为整数,若a和b被n除的余数相同,则称a和b对模n同余,记作a≡b(mod n).已知
D
A.2008 B.2009 C.2010 D.2011
2、求使2n+1能被3整除的一切自然数n.
则
2?-1 (mod3).
2x?(-1) x(mod3).
2n +1? (-1) n+ 1 (mod3).
∴
∴当n为奇数时,2n+1能被3整除;
当n为偶数时,2n+1不能被3整除.
解∵
3、 求2999最后两位数码(1990泰安高考题)
∴
又
∴
∴
∴ 2999的最后两位数字为88.
212 =4096? -4 (mod100).
2999 = (212)83 23 ? (-4)83 23 (mod100).
46 = 212 =4096 ? -4 (mod100).
483 = (46)13 45 ? (-4)13 25 ? - (46 ) 3 ? - (-4 ) 3 ? 64 (mod100).
2999 ? (-4)83 23 ? (-646 ) 23 ? - 2 9 ? -512 ? 88 (mod100).
解 考虑用100除2999所得的余数.
∵
1.2020年“五一节”是星期五,同年“国庆节”是星期( )
课堂练习
四
2.有一个数能被5整除,但除以4余3,这个正整数最小是( )
15
4.一个数除以3余2,除以4余1,那么这个数除以12,余数是( ).
5. 判定288和214对于模37是否同余?
解:∵ 288-214=74=37×2.
∴ 288≡214(mod37).
3.一个整数去除300,262,205,所得余数相同,这个整数是( )
A、19
B、9
C、15
D、12
A
A、1
B、2
C、3
D、5
D
分析 :若将结果乘出,结果会很大不利于计算,工作量大繁琐,所以利用学习的同余的性质可以使“大数化小”,减少计算量得出结果.
6. 求乘积418×814×1616除以13所得的余数.
解:∵418≡2(mod13),814≡8(mod13),
1616≡4(mod13),
∴ 根据同余的性质5可得:418×814×1616≡2×8×4≡64≡12( mod13)答:乘积418×814×1616除以13余数是12.
分析:求自然数的个位数字即是求这个自然数除以10的余数问题.
解:∵2100≡24×25≡625≡6(mod 10),
3101≡34×25·31≡125·31≡3(mod 10),
4102≡(22)100·42≡6·6≡6(mod 10),
∴2100+3101+4102≡6+3+6≡5(mod 10),
即自然数2100+3101+4102的个位数字是5.
7.求自然数2100+3101+4102的个位数字.
再见
知识回顾
16÷5=
5 16
)
3
15
1
3 ……1
除数
商
余数
被除数
导入新课
今天是星期日,再过15天就是“六·一”儿童节了,问“六·一”儿童节是星期几?
因为,一个星期有7天,而15÷7=2…1,即15=7×2+1,所以“六·一”儿童节是星期一.
解析:
2020年的元旦是星期三,2021年的元旦是星期几?
因为,2020年有366天,而366=7×52+2,所以,2021年的元旦应该是星期五.
解析:
下一节我们将学习利用余数来解决生活中的问题.
以上问题的实质是求用7去除以总的天数后所得的余数.在日常生活中,时常要注意两个整数用某一固定的自然数去除,所得的余数问题.
第二讲 同余与同余方程
第一节 同余
教学目标
知识与能力
1.理解同余概念与整除概念的联系,掌握同余的性质及应用.
2.并能灵活应用同余的基本性质解决具体问题.
3.灵活运用同余的性质解决现实生活中的实际问题.
过程与方法
情感态度与价值观
2.观察同余与整数之间的关系,并通过实例深化理解.
1.通过举例,引出同余的概念和记号.
培养学生结合以前所学知识,推导出新的知识或性质,有利于深刻理解.
教学重难点
重 点
1.准确理解同余的概念,正确的使用同余的符号.
难 点
2.类比等式的性质,探究证明同余的一些重要性质.
灵活运用同余的性质解决生活、理论中的实际问题.
12÷5=2…2
17÷5=3…2
22÷5=4…2
27÷5=5…2
32÷5=6…2
37÷5=7…2
……
被除数 除数 商 余数
12 5 2 2
17 5 3 2
22 5 4 2
27 5 5 2
32 5 6 2
37 5 7 2
… 5 … 2
观察上表有什么规律
通过观察,我们发现这些数被5整除后,得到的余数是相同的,这种情况我们成为模7同余.
一般地,设n为正整数,a和b为整数.如果a和b被n除后余数相同,那么称a和b模n同余,记作a ? b (mod n) .若a和b被n除后余数不同,则称a和b模n不同余,记作a b (mod n)
1)26和-14同时被4除判断他们的同余性,并用符号表示. 2)-14和22同时被4除判断他们的同余性,并用符号表示. 3)26和22同时被4除判断他们的同余性,并用符号表示. 4)26减去-14能否被4整除?
26÷4=4…2,
解析:
1)
-14÷4=-3…2
由定义知26和-14同余,故可写成
26 ? -14 (mod 4)
-14÷4=-3…2,
2)
22÷4=5…2
由定义知-14和22同余,故可写成
-14 ? 22 (mod 4)
-14 ? -26 (mod 4)
或
22 ? -14 (mod 4)
或
26÷4=4…2,
3)
22÷4=5…2
由定义知26和4同余,故可写成
26 ? 22 (mod 4)
26 ? 22 (mod 4)
或
解析:
4)
26-(-14) =40
4︱40
总结:
我们假设在上例中的a=26,b=-14,c=22,n=4.
-14 ? 22 (mod 4)
26 ? 22 (mod 4)
表示为:
1)
26 ? -14 (mod 4)
a ? b (mod n)
b ? c (mod n)
2)
3)
a ? c (mod n)
或
b ? a (mod n)
或
c ? b (mod n)
或
c ? a (mod n)
由以上实例可以总结出如下性质:
①自反性: a?a (mod n).
②对称性: 若a?b(mod n), 则b?a(mod n).
③传递性: 若a?b(mod n), b?c(mod n),
则: a?c(mod n).
④与整数的关系: a?b(mod n)
总结:
n︱a-b
若a?b(mod m), c?d(mod m), 则:
① ax+cy ? bx+dy(mod m), 其中x和y为任给整数.
② ac ? bd(mod m).
③ an ? bn(mod m), 其中 n>0.
④ f(a) ?f(b)(mod m), f(x)为任给的整系数多项式.
⑤ xa ?xb(mod m),x为任意整数.
探究
1、
若ab?ac(mod m), 且(a,n)=1,则b?c(mod m)
2、
性质应用
试求,17是否可以整除191000,若可以整除商是多少?余数是多少?
解:
因为
19 ? 2 (mod 17),
所以
191000 ? 21000 (mod 17) = 16250 (mod 17)
又因为
16 ? -1 (mod 17),
所以
16250 ? (- 1)250 (mod 17),
所以
17不能整除191000 ,余数为1
总结
在遇到很大的数时,我们很难直观判断余数是几,这时我们就要把被除数变小,降次,反复进行这个过程,直至求出结果.
如被除数为Ab (假设 Ab是一个很大的数),除数为C, 若C除以A余数为D,则Ab? Db (mod C) ;反复进行此过程直到求出结果.
课堂小结
同余定义
一般地,设n为正整数,a和b为整数.如果a和b被n除后余数相同,那么称a和b模n同余,记作a ? b (mod n) .若a和b被n除后余数不同,则称a和b模n不同余,记作a b (mod n)
由以上实例可以总结出如下性质:
①自反性: a?a (mod n).
②对称性: 若a?b(mod n), 则b?a(mod n).
③传递性: 若a?b(mod n), b?c(mod n),
则: a?c(mod n).
④与整数的关系: a?b(mod n)
n︱a-b
同余性质
若a?b(mod m), c?d(mod m), 则:
① ax+cy ? bx+dy(mod m), 其中x和y为任给整数.
② ac ? bd(mod m).
③ an ? bn(mod m), 其中 n>0.
④ f(a) ?f(b)(mod m), f(x)为任给的整系数多项式.
⑤ xa ?xb(mod m),x为任意整数.
1、
若ab?ac(mod m), 且(a,n)=1,则b?c(mod m)
2、
b≡a(mod 10),那么b的可能值是( )
针对性练习
1、设a、b、n(n>0)为整数,若a和b被n除的余数相同,则称a和b对模n同余,记作a≡b(mod n).已知
D
A.2008 B.2009 C.2010 D.2011
2、求使2n+1能被3整除的一切自然数n.
则
2?-1 (mod3).
2x?(-1) x(mod3).
2n +1? (-1) n+ 1 (mod3).
∴
∴当n为奇数时,2n+1能被3整除;
当n为偶数时,2n+1不能被3整除.
解∵
3、 求2999最后两位数码(1990泰安高考题)
∴
又
∴
∴
∴ 2999的最后两位数字为88.
212 =4096? -4 (mod100).
2999 = (212)83 23 ? (-4)83 23 (mod100).
46 = 212 =4096 ? -4 (mod100).
483 = (46)13 45 ? (-4)13 25 ? - (46 ) 3 ? - (-4 ) 3 ? 64 (mod100).
2999 ? (-4)83 23 ? (-646 ) 23 ? - 2 9 ? -512 ? 88 (mod100).
解 考虑用100除2999所得的余数.
∵
1.2020年“五一节”是星期五,同年“国庆节”是星期( )
课堂练习
四
2.有一个数能被5整除,但除以4余3,这个正整数最小是( )
15
4.一个数除以3余2,除以4余1,那么这个数除以12,余数是( ).
5. 判定288和214对于模37是否同余?
解:∵ 288-214=74=37×2.
∴ 288≡214(mod37).
3.一个整数去除300,262,205,所得余数相同,这个整数是( )
A、19
B、9
C、15
D、12
A
A、1
B、2
C、3
D、5
D
分析 :若将结果乘出,结果会很大不利于计算,工作量大繁琐,所以利用学习的同余的性质可以使“大数化小”,减少计算量得出结果.
6. 求乘积418×814×1616除以13所得的余数.
解:∵418≡2(mod13),814≡8(mod13),
1616≡4(mod13),
∴ 根据同余的性质5可得:418×814×1616≡2×8×4≡64≡12( mod13)答:乘积418×814×1616除以13余数是12.
分析:求自然数的个位数字即是求这个自然数除以10的余数问题.
解:∵2100≡24×25≡625≡6(mod 10),
3101≡34×25·31≡125·31≡3(mod 10),
4102≡(22)100·42≡6·6≡6(mod 10),
∴2100+3101+4102≡6+3+6≡5(mod 10),
即自然数2100+3101+4102的个位数字是5.
7.求自然数2100+3101+4102的个位数字.
再见
