人教版高中数学选修4-6 第四讲 数论在密码中的应用(二)大数分解和公开密匙 上课课件(共25张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第四讲 数论在密码中的应用(二)大数分解和公开密匙 上课课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 661.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:46:16 | ||
图片预览






文档简介
(共25张PPT)
知识回顾
一、什么是素数:仅有两个正因数的正整数.二、素数个数:素数有无数个. 三、信息加密传送方式:
传送方
加密
去密
接收方
信道
x
y=E(x)
D(y) = x
x
导入新课
将整数进行素数分解:
6 = 2×3 54=2×3×3×3 84=2×2×3×7
每个整数都可以分解成素因数的乘积,那你能把1589752654,甚至更大的数进行素因数分解吗?
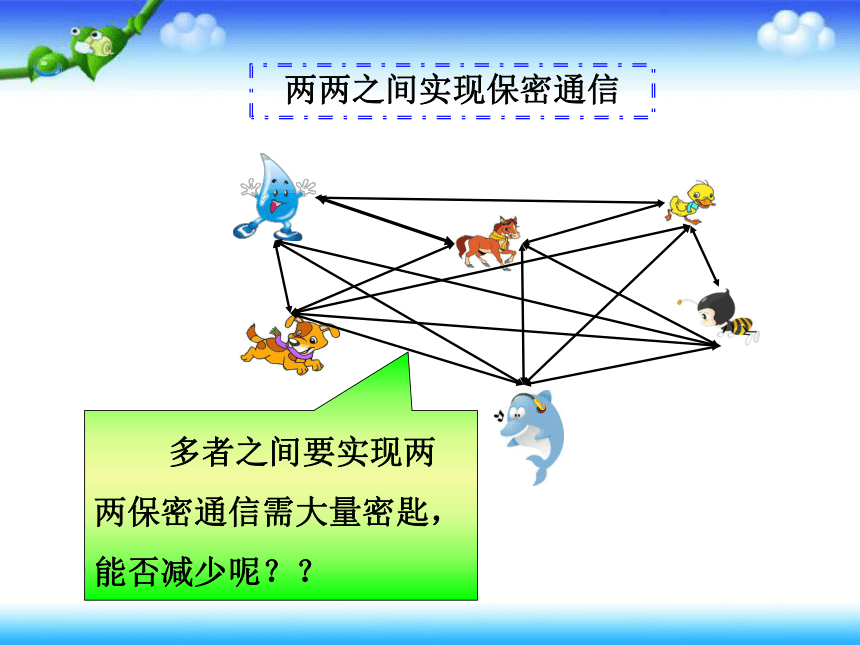
两两之间实现保密通信
多者之间要实现两两保密通信需大量密匙,能否减少呢??
上一节中我们已经知道若知道了加密运算 E(k),就能知道解密运算D(k), 即 E(k) D(k)
互逆
在知道E(k)时你能否对D(k)进行保密呢???
第四讲 数论在密码中的应用
第二节 大数分解和公开密匙
教学目标
知识与能力
一、了解公开密匙在生活总的重要地
位及其原理. 二、理解RSA方案在信息加密技术中
的应用. 三、掌握用公开密匙加密的信息传送
的数学模型.
过程与方法
情感态度与价值观
一、通过实例介绍公开密匙的重要性,引入公开密匙. 二、由以前学过的知识,介绍RSA方案.
提高学生对信息的安全保密意识,增加对信息安全技术的兴趣.
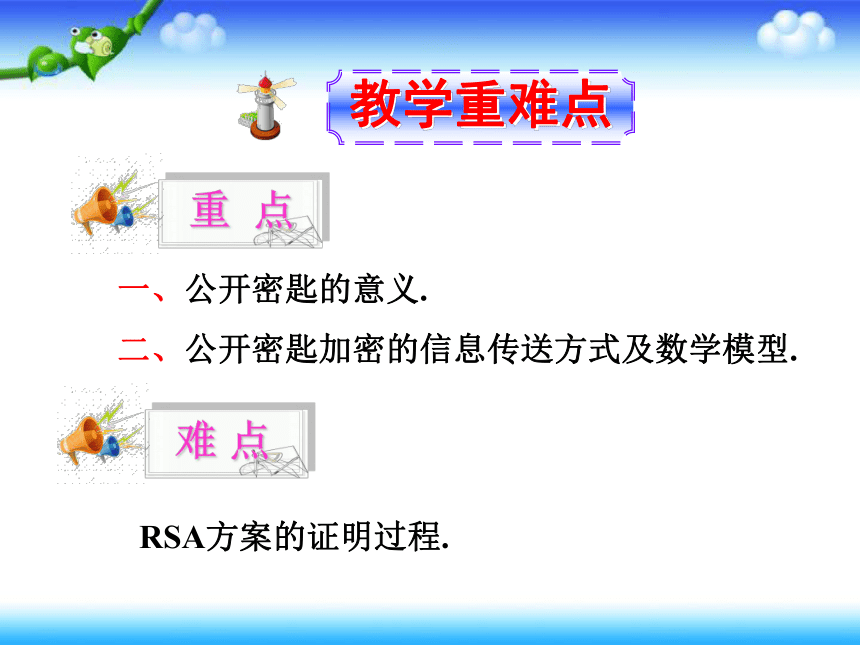
教学重难点
重 点
难 点
一、公开密匙的意义. 二、公开密匙加密的信息传送方式及数学模型.
RSA方案的证明过程.
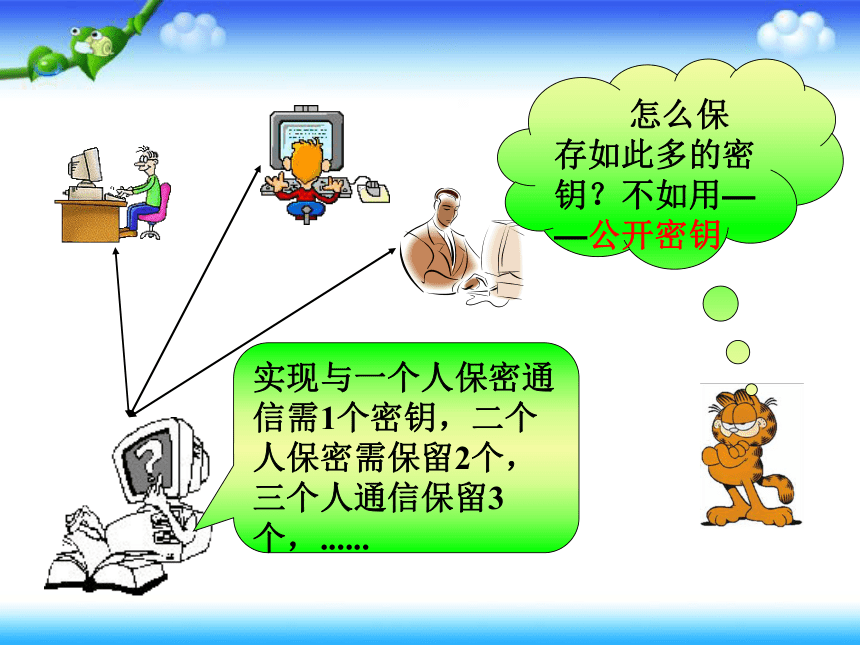
实现与一个人保密通信需1个密钥,二个人保密需保留2个,三个人通信保留3个,......
怎么保存如此多的密钥?不如用——公开密钥
公开密钥体制:信息的加密去密用两个不同的钥.
加 密:公钥(任何人可见)
去 密: 私钥(合法者拥有)
加 密 描 述: A用你的公钥将文件加密后发送给你,你收到文件后,用私钥解密,可打开文档;如别人截获了文件,但他没有你的私钥,所以解不了密.
这样只需保留2个密钥了.
将大合数分解成素因子乘积简称为大数分解.
大数分解
将合数分解成素因子乘积的形式.
合数 素因子乘积
12 2×2×3
58 2×29
1524 2×2×3×127
… ……
基于大数分解的公开密钥体系是——RSA方案.
选取不同素数p和q(均在100位左右),设n=pq, ? (n)=(p-1)(q-1),再取正整数e,d,使得ed≡1(mod ? (n) ) .
一般地,对上述正整数e,d和任意整数x,恒有xed ≡x(modn).
证明
证明:由 ed≡1(mod ? (n) )
知 ed=1 ? (n)k ,k∈z
若 p不能整除x,
那么 xed=x1+ ? (n)k =x·(xp-1)(q-1)k
若 p︱x,则xed和x模p均同余于0,
所以 对每个整数x,均有xed ≡x(mod p) 同理可证 xed ≡x(mod q)
因此 xed ≡x(modn)
RSA方案中,把信息x用0至n-1之间的数表示,公开密钥:E(x)≡xe(modn), 私人密钥:D(y) ≡yd(modn). 模型表示:
传送方
数字签名
加密
去密
身份认证
接收方
信道
x
y=D甲(x)
z=E乙(y)
y=D乙(z)
x=E甲(y)
x
x
课堂小结
一、RSA方案加密密钥: E(x)≡xe(modn)二、 RSA方案去密密钥: D(y) ≡yd(modn)三、公开密钥信息传送模型:
传送方
数字签名
加密
去密
身份认证
接收方
信道
x
y=D甲(x)
z=E乙(y)
y=D乙(z)
x=E甲(y)
x
x
针对性练习
一、设一RSA的公开加密钥为n = 943,e = 9,试将明文P = 100加密成密文E .
解: E ? 1009 ? 262 (mod 943),
即 E = 262,
又 943 = 23?41,p = 23,q = 41,
?(n) = 22?40 = 880,
由 9d ? 1 (mod 880)
解得 d = 489, 于是 P ? 262489 ? (748)244?262 ? (305)122?262
? (611)61?262? (836)30?715? (133)15?715
? (715)7?133?715 ? (715)8?133
? (119)4?133? (16)2?133? 256?133
? 100 (mod 943).
二、设RSA(nA, eA) = RSA(33, 3),RSA(nB, eB) = RSA(35, 5),A的签证信息为M = 3,试说明A向B发送签证M的传送和认证过程.
解:
因 A知dA = 7,eB = 5,
计算 E1 ? 37 ? 9 (mod 33),E ? 95 ? 4 (mod 35),
于是 A可将E = 04传送给B,
因 B知dB = 5,eA = 3,
计算 E1 ? 45 ? 9 (mod 35),M ? 93 ? 3 (mod 33),
于是 B认证了A的签证M = 03.
三、取p=11,q=13,求可能的一种公开密匙.
解:因为 p=11,q=13,
则 n=pq=11×13=143 ?
?(n)=(11-1)(13-1)=10 × 12=120
任取 ed≡1(mod120)
若取 e=1,则d=121,
由 E(x) ≡xe(modn)
得 E(x) ≡x1(mod143) 0≤x<143
课堂练习
一、取p=7,q=17,则 n=pq=7×17=119 ? ?(n)=(7-1)(17-1)=6 × 16=96 任取e等于5,则d等于( ).
二、取p=3,q=7,则 n=pq=3×7=21 ? ?(n)=(3-1)(7-1)=2 × 6=14 任取d等于3,则e等于( )
77
5
三、取n=pq=35 ?(n)=24则 p,q分别可以取( ).
A. p=1,q=35 B. p=4,q=6
C. p=35,q=1 D. p=5, q=7
四 、若公开密钥E(x)≡xe(mod124)则x的取值范围为( ).
A. 0≤x ≤ 124 B. 0≤x ≤ 123
C. x为任意整数 D. 0D
B
五、取p=17,q=7,求可能的一种公开密匙.
解:因为 p=17,q=7,
则 n=pq=17×7=119 ?
?(n)=(17-1)(7-1)=16 × 6=96
任取 ed≡1(mod96)
若取 e=1,则d=97,
由 E(x) ≡xe(modn)
得 E(x) ≡x1(mod143) 0≤x<119
解:
因为 p=3, q=5, 则 n=15,(p-1)*(q-1)=8 选取 e=11(大于p和q的质数), 由 d * 11 = 1 (mod 8), 得 d =3.
六、选取p=3, q=5,试计算出d和e分别是多少?假定明文为整数13,请给出密文数字.
解:假定明文为整数13,
则密文C为 (e为幂次方)
C = P e (mod 15 )
= 1792160394037 (mod 15 )= 7
复原明文P为: (d为幂次方)
P = Cd (mod 15 )= 343 (mod 15) = 13
七、选取p=3, q=5,若取d等于3和e等于11,假定明文为整数13,请给出密文数字.
再见
知识回顾
一、什么是素数:仅有两个正因数的正整数.二、素数个数:素数有无数个. 三、信息加密传送方式:
传送方
加密
去密
接收方
信道
x
y=E(x)
D(y) = x
x
导入新课
将整数进行素数分解:
6 = 2×3 54=2×3×3×3 84=2×2×3×7
每个整数都可以分解成素因数的乘积,那你能把1589752654,甚至更大的数进行素因数分解吗?
两两之间实现保密通信
多者之间要实现两两保密通信需大量密匙,能否减少呢??
上一节中我们已经知道若知道了加密运算 E(k),就能知道解密运算D(k), 即 E(k) D(k)
互逆
在知道E(k)时你能否对D(k)进行保密呢???
第四讲 数论在密码中的应用
第二节 大数分解和公开密匙
教学目标
知识与能力
一、了解公开密匙在生活总的重要地
位及其原理. 二、理解RSA方案在信息加密技术中
的应用. 三、掌握用公开密匙加密的信息传送
的数学模型.
过程与方法
情感态度与价值观
一、通过实例介绍公开密匙的重要性,引入公开密匙. 二、由以前学过的知识,介绍RSA方案.
提高学生对信息的安全保密意识,增加对信息安全技术的兴趣.
教学重难点
重 点
难 点
一、公开密匙的意义. 二、公开密匙加密的信息传送方式及数学模型.
RSA方案的证明过程.
实现与一个人保密通信需1个密钥,二个人保密需保留2个,三个人通信保留3个,......
怎么保存如此多的密钥?不如用——公开密钥
公开密钥体制:信息的加密去密用两个不同的钥.
加 密:公钥(任何人可见)
去 密: 私钥(合法者拥有)
加 密 描 述: A用你的公钥将文件加密后发送给你,你收到文件后,用私钥解密,可打开文档;如别人截获了文件,但他没有你的私钥,所以解不了密.
这样只需保留2个密钥了.
将大合数分解成素因子乘积简称为大数分解.
大数分解
将合数分解成素因子乘积的形式.
合数 素因子乘积
12 2×2×3
58 2×29
1524 2×2×3×127
… ……
基于大数分解的公开密钥体系是——RSA方案.
选取不同素数p和q(均在100位左右),设n=pq, ? (n)=(p-1)(q-1),再取正整数e,d,使得ed≡1(mod ? (n) ) .
一般地,对上述正整数e,d和任意整数x,恒有xed ≡x(modn).
证明
证明:由 ed≡1(mod ? (n) )
知 ed=1 ? (n)k ,k∈z
若 p不能整除x,
那么 xed=x1+ ? (n)k =x·(xp-1)(q-1)k
若 p︱x,则xed和x模p均同余于0,
所以 对每个整数x,均有xed ≡x(mod p) 同理可证 xed ≡x(mod q)
因此 xed ≡x(modn)
RSA方案中,把信息x用0至n-1之间的数表示,公开密钥:E(x)≡xe(modn), 私人密钥:D(y) ≡yd(modn). 模型表示:
传送方
数字签名
加密
去密
身份认证
接收方
信道
x
y=D甲(x)
z=E乙(y)
y=D乙(z)
x=E甲(y)
x
x
课堂小结
一、RSA方案加密密钥: E(x)≡xe(modn)二、 RSA方案去密密钥: D(y) ≡yd(modn)三、公开密钥信息传送模型:
传送方
数字签名
加密
去密
身份认证
接收方
信道
x
y=D甲(x)
z=E乙(y)
y=D乙(z)
x=E甲(y)
x
x
针对性练习
一、设一RSA的公开加密钥为n = 943,e = 9,试将明文P = 100加密成密文E .
解: E ? 1009 ? 262 (mod 943),
即 E = 262,
又 943 = 23?41,p = 23,q = 41,
?(n) = 22?40 = 880,
由 9d ? 1 (mod 880)
解得 d = 489, 于是 P ? 262489 ? (748)244?262 ? (305)122?262
? (611)61?262? (836)30?715? (133)15?715
? (715)7?133?715 ? (715)8?133
? (119)4?133? (16)2?133? 256?133
? 100 (mod 943).
二、设RSA(nA, eA) = RSA(33, 3),RSA(nB, eB) = RSA(35, 5),A的签证信息为M = 3,试说明A向B发送签证M的传送和认证过程.
解:
因 A知dA = 7,eB = 5,
计算 E1 ? 37 ? 9 (mod 33),E ? 95 ? 4 (mod 35),
于是 A可将E = 04传送给B,
因 B知dB = 5,eA = 3,
计算 E1 ? 45 ? 9 (mod 35),M ? 93 ? 3 (mod 33),
于是 B认证了A的签证M = 03.
三、取p=11,q=13,求可能的一种公开密匙.
解:因为 p=11,q=13,
则 n=pq=11×13=143 ?
?(n)=(11-1)(13-1)=10 × 12=120
任取 ed≡1(mod120)
若取 e=1,则d=121,
由 E(x) ≡xe(modn)
得 E(x) ≡x1(mod143) 0≤x<143
课堂练习
一、取p=7,q=17,则 n=pq=7×17=119 ? ?(n)=(7-1)(17-1)=6 × 16=96 任取e等于5,则d等于( ).
二、取p=3,q=7,则 n=pq=3×7=21 ? ?(n)=(3-1)(7-1)=2 × 6=14 任取d等于3,则e等于( )
77
5
三、取n=pq=35 ?(n)=24则 p,q分别可以取( ).
A. p=1,q=35 B. p=4,q=6
C. p=35,q=1 D. p=5, q=7
四 、若公开密钥E(x)≡xe(mod124)则x的取值范围为( ).
A. 0≤x ≤ 124 B. 0≤x ≤ 123
C. x为任意整数 D. 0
B
五、取p=17,q=7,求可能的一种公开密匙.
解:因为 p=17,q=7,
则 n=pq=17×7=119 ?
?(n)=(17-1)(7-1)=16 × 6=96
任取 ed≡1(mod96)
若取 e=1,则d=97,
由 E(x) ≡xe(modn)
得 E(x) ≡x1(mod143) 0≤x<119
解:
因为 p=3, q=5, 则 n=15,(p-1)*(q-1)=8 选取 e=11(大于p和q的质数), 由 d * 11 = 1 (mod 8), 得 d =3.
六、选取p=3, q=5,试计算出d和e分别是多少?假定明文为整数13,请给出密文数字.
解:假定明文为整数13,
则密文C为 (e为幂次方)
C = P e (mod 15 )
= 1792160394037 (mod 15 )= 7
复原明文P为: (d为幂次方)
P = Cd (mod 15 )= 343 (mod 15) = 13
七、选取p=3, q=5,若取d等于3和e等于11,假定明文为整数13,请给出密文数字.
再见
