人教版高中数学选修4-6 第一讲 整数的整除(一)整数的整除 上课课件(共33张PPT)
文档属性
| 名称 | 人教版高中数学选修4-6 第一讲 整数的整除(一)整数的整除 上课课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 687.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:56:40 | ||
图片预览










文档简介
(共33张PPT)
知识回顾
以前学过的整数加法、减法、乘法有什么特点?整数除法的商又是怎样的?
整数的加法、减法、乘法运算得到的结果任然为整数.两个整数的商不一定是整数.
导入新课
从以前学过的乘法中我们知道若A×B=C,那么C÷B=A或C÷A=B
例如:
13×2 = 26
也就是说乘法和除法是互逆的运算.
26÷2 = 13
26÷13 = 2
共六条鱼,平均一只猫咪得几条鱼?
若是再多一条鱼,平均一只猫咪又各得几条鱼呢?
;第二种
在上一页第一种情况下,平均每只猫咪得到
想一想
6÷2 = 3(条)
情况下每只猫咪在得到3条鱼后还剩一条,就是说这种情况下鱼并不能平均分给两只猫咪.
生活中这样的例子还有很多,我们从数学的角度该怎样理解,又怎样定义呢?它们又有怎样的性质?下面我们将具体的分析.
第一讲整数的整除
第一节 整 除
教学目标
知识与能力
1.在熟悉整数的基础上充分理解整除的概念和性质;熟练掌握带余除法的运算,且能进行运算.
2.理解什么是素数的概念,并掌握素数的判别方法.
过程与方法
1.通过复习以前的乘法、除法的知识,让学生合作探讨,老师启迪,自然引出整除的概念及性质.
2.在整除的基础上通过生活中的实例,引导学生考虑不能整除的情况,并让学生自己进一步思考不能整除情况的解决方法并总结带余除法的概念.
3.通过将大化小,让学生自由讨论,教师恰如其分的指出素数.
情感态度与价值观
1.通过对整除的认识和学习,能够体会数学中的联系与结合,有利于理解和掌握.
2.将知识应用到现实生活中.
3.培养合作交流意识.
教学重难点
重点
难点
整除、公因子、素数的概念及性质,剩余定理,求最大公因子的方法,整数的素数分解定理.
函数[x]、{x}的概念及其应用.
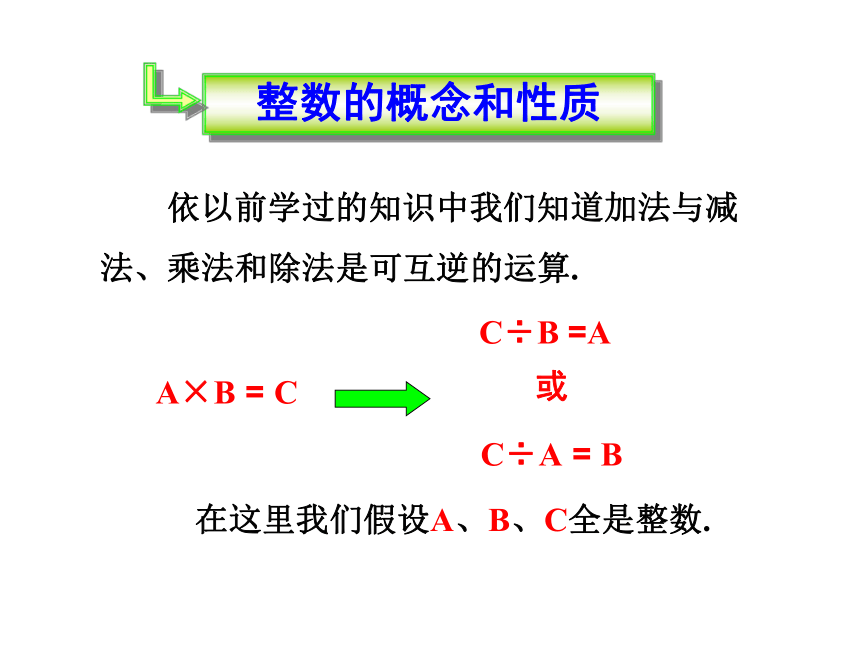
整数的概念和性质
依以前学过的知识中我们知道加法与减法、乘法和除法是可互逆的运算.
A×B = C
C÷B =A
C÷A = B
或
在这里我们假设A、B、C全是整数.
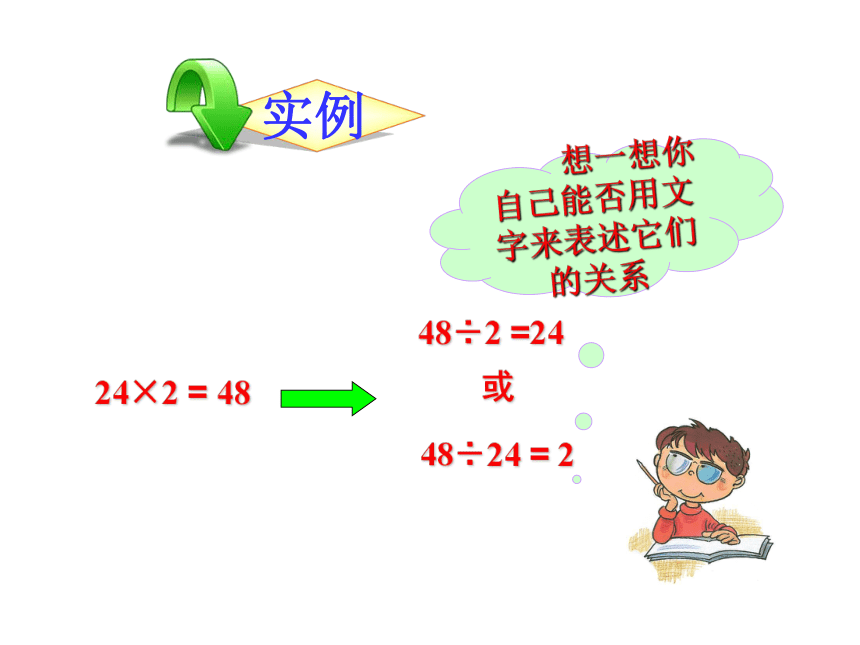
实例
24×2 = 48
48÷2 =24
48÷24 = 2
或
想一想你自己能否用文字来表述它们的关系
一般地,设a, b为整数,且b ≠0.如果存在q ,使得a = b q ,那么称b整除a ,或者a能被b整除,记做b | a .并且称b是a的因数, a是b的倍数.如果这样的整数q不存在,就称b不整除a ,记做b a.
整除的概念
小练习
根据整除的概念判断下列式子正确与否:
(1) 3|-9
(2) 2|4
(3) -2|6
(3) 5|16
( )
( )
( )
( )
√
√
√
×
能被非零整数n整除的数是n的倍数,能整除n的整数是n的因数.
总结
如12可被2整除,12是2的倍数,2是12的因数.
想一想4的所有因数有哪些
观察
12,21,24,30,33,51可同时被什么数整除,有什么规律?
分析:以上6个数均可同时被3整除,并且各位数字之和也能被3整除.
由此猜想:一个正整数的各位数字之和能被3整除,那么这个正整数能被3整除.
带余除法
在生活中并不是什么情况下都可以整除,很多情况都是不能除尽的.如:13÷2=6…1,在整数集中这种表示法依然成立,叫做带余除法(或欧氏除法算式).
一般地,设a,b为整数,且b≠0 ,则存在惟一的一对整数q和r,使得a=bq+r,0≤r<︱b︱.
实例
32除以某个整数,其商为5,求除数和余数.
解析:
解:设除数为b,余数为r则
32=5b+r,0≤r<b.
由此可得
5b ≤ 32<6b
所以
32/6 < b ≤ 32/5
因此
b=6,r=2
素数及其判别方法
自然数 正 因 数
1
2
5
9
11
12
17
20
1
1、2
1、5
1、3、9
1、11
1、2、3、4、6、12
1、17
1、2、4、5、10、20
★只有一个约数的:
( )
★只有两个约数的:
( )
★有两个以上约数的:
( )
1
2、5、11、17
9、12、20
仅有两个正因数的正整数叫做素数,不是素数又不是1的正整数叫做合数.1既不是素数,也不是合数.
自然数
素数
合数
1
定义
如:3的正因数只有1和3所以3为素数;6的正因数有1、2、3、6所以由定义知6为合数.
实例
思考:最小的素数和最小的合数各是几?
最小的素数是:2
最小的合数是:4
想一想如何判断一个数是不是素数
如果大于1的整数a不能被所有不超过
的素数整
除,那么a一定是素数.
埃拉托斯特尼筛法
课堂小结
如果存在q,使得ɑ=bq,那么称b整除ɑ.记作: b|ɑ
1、整除的概念
2、整除的性质
1)若a|b,a|c,则a|(b±c);
2)若a|b,b|c,则a|c;
3)若a|bc,且(a,c)=1,则a|b,特别地,若质数p|bc,则必有p|b或p|c;
4)若b|a,c|a,且(b,c)=1,则bc|a
解整除有关问题常用到数的整除性常见特征:
1.被2整除的数:个位数字是偶数;
2.被5整除的数:个位数字是0或5;
3.被4整除的数:末两位组成的数被4整除;
被25整除的数: 末两位组成的被25整除;
4.被8整除的数:末三位组成的数被8整除;
被125整除的数:末三位组成的被125整除;
5.被3整除的数:数字和被3整除;
6.被9整除的数:数字和被9整除;
7.被11整除的数:奇数位数字和与偶数位数字和 的差被11整除.
4、素数定义
仅有两个正因数的正整数叫做素数,不是素数又不是1的正整数叫做合数.
3、带余除法定义
一般地,设a,b为整数,且b≠0 ,则存在惟一的一对整数q和r,使得a=bq+r,0≤r<︱b︱.
针对性练习
1、9192除以100的余数_____________.
由此可见,除后两项外均能被100整除.
分析:
故9192被100整除余数是81.
81
2、已知i,m,n是正整数,且1<i≤m<n.
证明:(1+m)n>(1+n)m.
证明:
(1+m)n=miC,
(1+n)m=niC.
由(1)知niA<miA,
又 = , = ,
∴ ni <mi (1<i≤m<n),
故 ni < mi ,
又n0 =m0 ,n =mn=m .
∴ ni < mi ,
即(1+n)m<(1+m)n.
3、如果今天是星期一,那么对于任意的正整数n,经过23n+3+7n+5天后的那一天是星期几?
由题意知,就是求 23n+3+7n+5被7除时的余数.
解: 实质是求23n+3+7n+5被7除时的余数.
∵ 7n能被7整除,5被7除时的余数为5,
∴ 23n+3+7n+5被7除时的余数为6.
∴ 经过23n+3+7n+5天后的那一天是星期日.
【思考与分析】
课堂练习
1、一个自然数与13的和是5的倍数,与 13的差是6的倍数,则满足条件的最小自然数是_____________.
37
2、一个自然数N被10除余9,被9除余8,被8除余7,被7除余6,被6除余5,被5除余4,被3除余2,被2除余1,则N的最小值是___________.
2519
3、若1059、1417、2321分别被自然数x除时,得的余数都是y,则x-y的值等于( ).
A.15 B. 1 C.164 D.174
A
4、有自然数带余除法算式:A÷B=C…8,如果A+B+C=2178,那么A= ( )
A.2001 B.2000 C.2071 D.2100
B
5、若a、b、c、d是互不相等的整数,且整数x满足等式(x-a)(x-b)(x-c)(x-d)-9=0,求证:4|(a+b+c+d).
x-a,x-b, x-c,x-d是互不相等的整数,且它们的乘积等于9,于是必须把9分解为4个互不相等的因数的积;
【思考点拨】
6、已知两个三位数abc与def的和abc+def能被37整除,证明:六位数也能被37整除.
因已知条件的数是三位数,故应设法把六位数abcdef用三位数的形式表示,以沟通已知与求证结论的联系.
【思考点拨】
7、已知7位数1287xy6是72的倍数,求出所有的符合条件的7位数.
7位数1287xy6能被8,9整除,运用整数能被8、9整除的性质求出x,y的值.
【思考点拨】
再见
知识回顾
以前学过的整数加法、减法、乘法有什么特点?整数除法的商又是怎样的?
整数的加法、减法、乘法运算得到的结果任然为整数.两个整数的商不一定是整数.
导入新课
从以前学过的乘法中我们知道若A×B=C,那么C÷B=A或C÷A=B
例如:
13×2 = 26
也就是说乘法和除法是互逆的运算.
26÷2 = 13
26÷13 = 2
共六条鱼,平均一只猫咪得几条鱼?
若是再多一条鱼,平均一只猫咪又各得几条鱼呢?
;第二种
在上一页第一种情况下,平均每只猫咪得到
想一想
6÷2 = 3(条)
情况下每只猫咪在得到3条鱼后还剩一条,就是说这种情况下鱼并不能平均分给两只猫咪.
生活中这样的例子还有很多,我们从数学的角度该怎样理解,又怎样定义呢?它们又有怎样的性质?下面我们将具体的分析.
第一讲整数的整除
第一节 整 除
教学目标
知识与能力
1.在熟悉整数的基础上充分理解整除的概念和性质;熟练掌握带余除法的运算,且能进行运算.
2.理解什么是素数的概念,并掌握素数的判别方法.
过程与方法
1.通过复习以前的乘法、除法的知识,让学生合作探讨,老师启迪,自然引出整除的概念及性质.
2.在整除的基础上通过生活中的实例,引导学生考虑不能整除的情况,并让学生自己进一步思考不能整除情况的解决方法并总结带余除法的概念.
3.通过将大化小,让学生自由讨论,教师恰如其分的指出素数.
情感态度与价值观
1.通过对整除的认识和学习,能够体会数学中的联系与结合,有利于理解和掌握.
2.将知识应用到现实生活中.
3.培养合作交流意识.
教学重难点
重点
难点
整除、公因子、素数的概念及性质,剩余定理,求最大公因子的方法,整数的素数分解定理.
函数[x]、{x}的概念及其应用.
整数的概念和性质
依以前学过的知识中我们知道加法与减法、乘法和除法是可互逆的运算.
A×B = C
C÷B =A
C÷A = B
或
在这里我们假设A、B、C全是整数.
实例
24×2 = 48
48÷2 =24
48÷24 = 2
或
想一想你自己能否用文字来表述它们的关系
一般地,设a, b为整数,且b ≠0.如果存在q ,使得a = b q ,那么称b整除a ,或者a能被b整除,记做b | a .并且称b是a的因数, a是b的倍数.如果这样的整数q不存在,就称b不整除a ,记做b a.
整除的概念
小练习
根据整除的概念判断下列式子正确与否:
(1) 3|-9
(2) 2|4
(3) -2|6
(3) 5|16
( )
( )
( )
( )
√
√
√
×
能被非零整数n整除的数是n的倍数,能整除n的整数是n的因数.
总结
如12可被2整除,12是2的倍数,2是12的因数.
想一想4的所有因数有哪些
观察
12,21,24,30,33,51可同时被什么数整除,有什么规律?
分析:以上6个数均可同时被3整除,并且各位数字之和也能被3整除.
由此猜想:一个正整数的各位数字之和能被3整除,那么这个正整数能被3整除.
带余除法
在生活中并不是什么情况下都可以整除,很多情况都是不能除尽的.如:13÷2=6…1,在整数集中这种表示法依然成立,叫做带余除法(或欧氏除法算式).
一般地,设a,b为整数,且b≠0 ,则存在惟一的一对整数q和r,使得a=bq+r,0≤r<︱b︱.
实例
32除以某个整数,其商为5,求除数和余数.
解析:
解:设除数为b,余数为r则
32=5b+r,0≤r<b.
由此可得
5b ≤ 32<6b
所以
32/6 < b ≤ 32/5
因此
b=6,r=2
素数及其判别方法
自然数 正 因 数
1
2
5
9
11
12
17
20
1
1、2
1、5
1、3、9
1、11
1、2、3、4、6、12
1、17
1、2、4、5、10、20
★只有一个约数的:
( )
★只有两个约数的:
( )
★有两个以上约数的:
( )
1
2、5、11、17
9、12、20
仅有两个正因数的正整数叫做素数,不是素数又不是1的正整数叫做合数.1既不是素数,也不是合数.
自然数
素数
合数
1
定义
如:3的正因数只有1和3所以3为素数;6的正因数有1、2、3、6所以由定义知6为合数.
实例
思考:最小的素数和最小的合数各是几?
最小的素数是:2
最小的合数是:4
想一想如何判断一个数是不是素数
如果大于1的整数a不能被所有不超过
的素数整
除,那么a一定是素数.
埃拉托斯特尼筛法
课堂小结
如果存在q,使得ɑ=bq,那么称b整除ɑ.记作: b|ɑ
1、整除的概念
2、整除的性质
1)若a|b,a|c,则a|(b±c);
2)若a|b,b|c,则a|c;
3)若a|bc,且(a,c)=1,则a|b,特别地,若质数p|bc,则必有p|b或p|c;
4)若b|a,c|a,且(b,c)=1,则bc|a
解整除有关问题常用到数的整除性常见特征:
1.被2整除的数:个位数字是偶数;
2.被5整除的数:个位数字是0或5;
3.被4整除的数:末两位组成的数被4整除;
被25整除的数: 末两位组成的被25整除;
4.被8整除的数:末三位组成的数被8整除;
被125整除的数:末三位组成的被125整除;
5.被3整除的数:数字和被3整除;
6.被9整除的数:数字和被9整除;
7.被11整除的数:奇数位数字和与偶数位数字和 的差被11整除.
4、素数定义
仅有两个正因数的正整数叫做素数,不是素数又不是1的正整数叫做合数.
3、带余除法定义
一般地,设a,b为整数,且b≠0 ,则存在惟一的一对整数q和r,使得a=bq+r,0≤r<︱b︱.
针对性练习
1、9192除以100的余数_____________.
由此可见,除后两项外均能被100整除.
分析:
故9192被100整除余数是81.
81
2、已知i,m,n是正整数,且1<i≤m<n.
证明:(1+m)n>(1+n)m.
证明:
(1+m)n=miC,
(1+n)m=niC.
由(1)知niA<miA,
又 = , = ,
∴ ni <mi (1<i≤m<n),
故 ni < mi ,
又n0 =m0 ,n =mn=m .
∴ ni < mi ,
即(1+n)m<(1+m)n.
3、如果今天是星期一,那么对于任意的正整数n,经过23n+3+7n+5天后的那一天是星期几?
由题意知,就是求 23n+3+7n+5被7除时的余数.
解: 实质是求23n+3+7n+5被7除时的余数.
∵ 7n能被7整除,5被7除时的余数为5,
∴ 23n+3+7n+5被7除时的余数为6.
∴ 经过23n+3+7n+5天后的那一天是星期日.
【思考与分析】
课堂练习
1、一个自然数与13的和是5的倍数,与 13的差是6的倍数,则满足条件的最小自然数是_____________.
37
2、一个自然数N被10除余9,被9除余8,被8除余7,被7除余6,被6除余5,被5除余4,被3除余2,被2除余1,则N的最小值是___________.
2519
3、若1059、1417、2321分别被自然数x除时,得的余数都是y,则x-y的值等于( ).
A.15 B. 1 C.164 D.174
A
4、有自然数带余除法算式:A÷B=C…8,如果A+B+C=2178,那么A= ( )
A.2001 B.2000 C.2071 D.2100
B
5、若a、b、c、d是互不相等的整数,且整数x满足等式(x-a)(x-b)(x-c)(x-d)-9=0,求证:4|(a+b+c+d).
x-a,x-b, x-c,x-d是互不相等的整数,且它们的乘积等于9,于是必须把9分解为4个互不相等的因数的积;
【思考点拨】
6、已知两个三位数abc与def的和abc+def能被37整除,证明:六位数也能被37整除.
因已知条件的数是三位数,故应设法把六位数abcdef用三位数的形式表示,以沟通已知与求证结论的联系.
【思考点拨】
7、已知7位数1287xy6是72的倍数,求出所有的符合条件的7位数.
7位数1287xy6能被8,9整除,运用整数能被8、9整除的性质求出x,y的值.
【思考点拨】
再见
