沪科版七下数学8.1 同底数幂的乘法教学课件(25张PPT)
文档属性
| 名称 | 沪科版七下数学8.1 同底数幂的乘法教学课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 847.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
8.1 幂的运算
同底数幂的乘法
第8章 整式的乘法与因式分解
1
课堂讲解
同底数幂的乘法的法则
同底数幂的乘法法则的拓展与灵活应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
光年是长度单位,1光年是指光经过一年所行的距
离. 光的速度大3×105km/s,若1年以365天计,则1光年大约是多少千米?
1
知识点
同底数幂的乘法的法则
我国首台千万亿次超级计算机系统“天河一号” 计算机每秒可进行2.57×1015次运算,问它工作1 h (3.6×103 s)可进行多少次运算?
2.57×1015× 3.6×103
=2.57× 3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
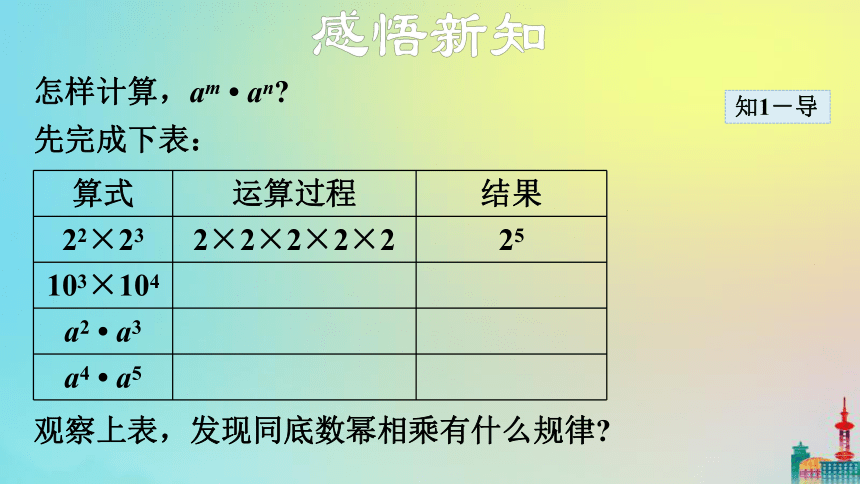
怎样计算,am ? an?
先完成下表:
观察上表,发现同底数幂相乘有什么规律?
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2 ? a3
a4 ? a5
一般地,如果字母m,n都是正整数,那么
am ? an = (a ? a ? … ? a) ? (a ? a ? … ? a)
=a ? a ? … ? a
=am+n .
(m + n)个
m 个
n个
1. 同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即:am·an=am+n(m,n都是正整数).
2. 要点精析:
(1) 同底数幂的乘法法则只有在底数相同时才能使用, 并且底数不变,指数相加,而不是指数相乘.
(2) 不同底数要先化成同底数.
(3) 单个字母或数可以看作指数为1的幂,参与同底数幂的运算时,不能忽略了幂指数1.
计算:(1)a2·a3·a·a5;(2)-a3·a4;(3)a2·(-a)5.
例1
导引:
紧扣同底数幂的乘法法则,先看是否符合同底数的幂相乘,再按法则计算.
解:
(1) a2·a3·a·a5=a2+3+1+5=a11;
(2) -a3·a4=-a3+4=-a7;
(3) a2·(-a)5=a2·(-a5)=-a2+5=-a7.
计算:
(1) ; (2) (-2)2×(-2)7 ;
(3) a2·a3·a6; (4) (-y)3· y4.
例2
解:
(1) ;
(2) (-2)2×(-2)7 =(-2)2+7=(-2)9 =-29 ;
(3) a2·a3·a6 =a2+3+6=a11;
(4) (-y)3· y4= -y3· y4= -y3+4 = -y7.
同底数幂相乘,首先确定符号,负因数出现奇数个就取负号,出现偶数个就取正号,然后按照同底数幂的乘法法则进行计算.
1
(中考·泸州)计算x2·x3的结果为( )
A.2x2 B.x5
C.2x3 D.x6
计算(-a)3·(-a)2的结果是( )
A.a5 B.-a5
C.a6 D.-a6
2
B
B
2
知识点
同底数幂的乘法法则的应用
(1)同底数幂的乘法法则对于三个同底数幂相乘同 样适用.
即:am·an·ap=am+n+p(m,n,p都是正整数).
(2)同底数幂的乘法法则可逆用,即am+n=am·an
(m,n都是正整数).
(3)底数可以是一个单项式,也可以是一个多项式; 在幂的运算中常用到下面两种变形:
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
②(a-b)n=
计算:(1)(x-y)3·(y-x)5;
(2)(x-y)3·(x-y)2·(y-x);
(3)(a-b)3·(b-a)4.
例3
导引:
先将不是同底数的幂转化为同底数的幂,再运用法则计算.
(1)(x-y)3·(y-x)5=(x-y)3·[-(x-y)5]
=-(x-y)3+5
=-(x-y)8.
(2)(x-y)3·(x-y)2·(y-x)=(x-y)3·(x-y)2·[-(x-y)]
=-(x-y)3+2+1=-(x-y)6.
(3)(a-b)3·(b-a)4=(a-b)3·(a-b)4=(a-b)3+4
=(a-b)7.
解:
底数互为相反数的幂相乘时,可以利用幂确定符号的方法先转化为同底数幂,再按法则计算,统一底数时尽可能地改变偶次幂的底数,这样可以减少符号的变化.
已知2x=5,求2x+2的值.
例4
分析:
根据同底数幂的乘法法则,am?an=am+n(m,n为正整数),反之,am+n= am?an,即逆用法则求值.
2x+2=2x?22=5×4 =20.
解:
要灵活利用公式或逆用公式是计算简单.
计算:
(1)103×10+100×102;(2)x3·xm-xm+3.
例5
导引:
先算同底数幂的乘法,再合并同类项.
(1)103×10+100×102=104+104=2×104.
(2) x3·xm-xm+3=x3+m-xm+3=0.
解:
和有理数的运算顺序一致,含有幂的乘法的混合运算中,先算同底数幂的乘法,再算整式的加减.
1. 运用同底数幂的乘法法则时,注意成立的条件是同底.遇到底数不同的情况可以通过变换转化为底数相同的,然后运用法则进行计算.
2. 同底数幂的乘法法则对三个或三个以上的同底数幂的乘法同样适用,底数可以是单项式,也可以是多项式.
3. 同底数幂的乘法法则可以正用,也可以逆用,am+n =am·an (m,n都是正整数).
1. 必做:完成教材P46练习T1-T2,
完成教材P54习题8.1T1
8.1 幂的运算
同底数幂的乘法
第8章 整式的乘法与因式分解
1
课堂讲解
同底数幂的乘法的法则
同底数幂的乘法法则的拓展与灵活应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
光年是长度单位,1光年是指光经过一年所行的距
离. 光的速度大3×105km/s,若1年以365天计,则1光年大约是多少千米?
1
知识点
同底数幂的乘法的法则
我国首台千万亿次超级计算机系统“天河一号” 计算机每秒可进行2.57×1015次运算,问它工作1 h (3.6×103 s)可进行多少次运算?
2.57×1015× 3.6×103
=2.57× 3.6×1015×103
=?
解决这个问题需要研究同底数幂的乘法.
怎样计算,am ? an?
先完成下表:
观察上表,发现同底数幂相乘有什么规律?
算式 运算过程 结果
22×23 2×2×2×2×2 25
103×104
a2 ? a3
a4 ? a5
一般地,如果字母m,n都是正整数,那么
am ? an = (a ? a ? … ? a) ? (a ? a ? … ? a)
=a ? a ? … ? a
=am+n .
(m + n)个
m 个
n个
1. 同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即:am·an=am+n(m,n都是正整数).
2. 要点精析:
(1) 同底数幂的乘法法则只有在底数相同时才能使用, 并且底数不变,指数相加,而不是指数相乘.
(2) 不同底数要先化成同底数.
(3) 单个字母或数可以看作指数为1的幂,参与同底数幂的运算时,不能忽略了幂指数1.
计算:(1)a2·a3·a·a5;(2)-a3·a4;(3)a2·(-a)5.
例1
导引:
紧扣同底数幂的乘法法则,先看是否符合同底数的幂相乘,再按法则计算.
解:
(1) a2·a3·a·a5=a2+3+1+5=a11;
(2) -a3·a4=-a3+4=-a7;
(3) a2·(-a)5=a2·(-a5)=-a2+5=-a7.
计算:
(1) ; (2) (-2)2×(-2)7 ;
(3) a2·a3·a6; (4) (-y)3· y4.
例2
解:
(1) ;
(2) (-2)2×(-2)7 =(-2)2+7=(-2)9 =-29 ;
(3) a2·a3·a6 =a2+3+6=a11;
(4) (-y)3· y4= -y3· y4= -y3+4 = -y7.
同底数幂相乘,首先确定符号,负因数出现奇数个就取负号,出现偶数个就取正号,然后按照同底数幂的乘法法则进行计算.
1
(中考·泸州)计算x2·x3的结果为( )
A.2x2 B.x5
C.2x3 D.x6
计算(-a)3·(-a)2的结果是( )
A.a5 B.-a5
C.a6 D.-a6
2
B
B
2
知识点
同底数幂的乘法法则的应用
(1)同底数幂的乘法法则对于三个同底数幂相乘同 样适用.
即:am·an·ap=am+n+p(m,n,p都是正整数).
(2)同底数幂的乘法法则可逆用,即am+n=am·an
(m,n都是正整数).
(3)底数可以是一个单项式,也可以是一个多项式; 在幂的运算中常用到下面两种变形:
①(-a)n=
an(n为偶数)
-an(n为奇数)
(b-a)n(n为偶数)
-(b-a)n(n为奇数)
②(a-b)n=
计算:(1)(x-y)3·(y-x)5;
(2)(x-y)3·(x-y)2·(y-x);
(3)(a-b)3·(b-a)4.
例3
导引:
先将不是同底数的幂转化为同底数的幂,再运用法则计算.
(1)(x-y)3·(y-x)5=(x-y)3·[-(x-y)5]
=-(x-y)3+5
=-(x-y)8.
(2)(x-y)3·(x-y)2·(y-x)=(x-y)3·(x-y)2·[-(x-y)]
=-(x-y)3+2+1=-(x-y)6.
(3)(a-b)3·(b-a)4=(a-b)3·(a-b)4=(a-b)3+4
=(a-b)7.
解:
底数互为相反数的幂相乘时,可以利用幂确定符号的方法先转化为同底数幂,再按法则计算,统一底数时尽可能地改变偶次幂的底数,这样可以减少符号的变化.
已知2x=5,求2x+2的值.
例4
分析:
根据同底数幂的乘法法则,am?an=am+n(m,n为正整数),反之,am+n= am?an,即逆用法则求值.
2x+2=2x?22=5×4 =20.
解:
要灵活利用公式或逆用公式是计算简单.
计算:
(1)103×10+100×102;(2)x3·xm-xm+3.
例5
导引:
先算同底数幂的乘法,再合并同类项.
(1)103×10+100×102=104+104=2×104.
(2) x3·xm-xm+3=x3+m-xm+3=0.
解:
和有理数的运算顺序一致,含有幂的乘法的混合运算中,先算同底数幂的乘法,再算整式的加减.
1. 运用同底数幂的乘法法则时,注意成立的条件是同底.遇到底数不同的情况可以通过变换转化为底数相同的,然后运用法则进行计算.
2. 同底数幂的乘法法则对三个或三个以上的同底数幂的乘法同样适用,底数可以是单项式,也可以是多项式.
3. 同底数幂的乘法法则可以正用,也可以逆用,am+n =am·an (m,n都是正整数).
1. 必做:完成教材P46练习T1-T2,
完成教材P54习题8.1T1
