北师大版高中数学必修五第三章《简单线性规划的应用》课件(共20张PPT)
文档属性
| 名称 | 北师大版高中数学必修五第三章《简单线性规划的应用》课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:57:30 | ||
图片预览






文档简介
(共20张PPT)
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修5 第三章 不等式 §4.3 简单线性规划的应用
复习引入
解析答案
反思与感悟
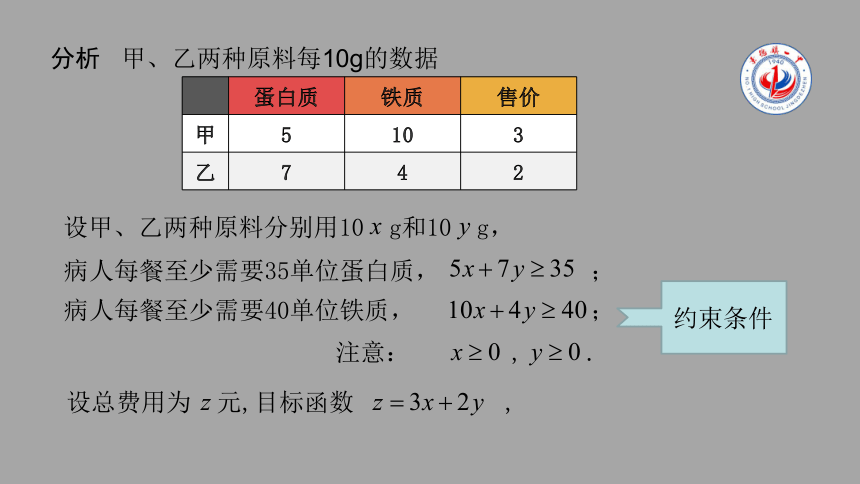
例1 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元. 若病人每餐至少需要35单位蛋白质和40单位铁质. 试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?
解析答案
反思与感悟
分析 甲、乙两种原料每10g的数据
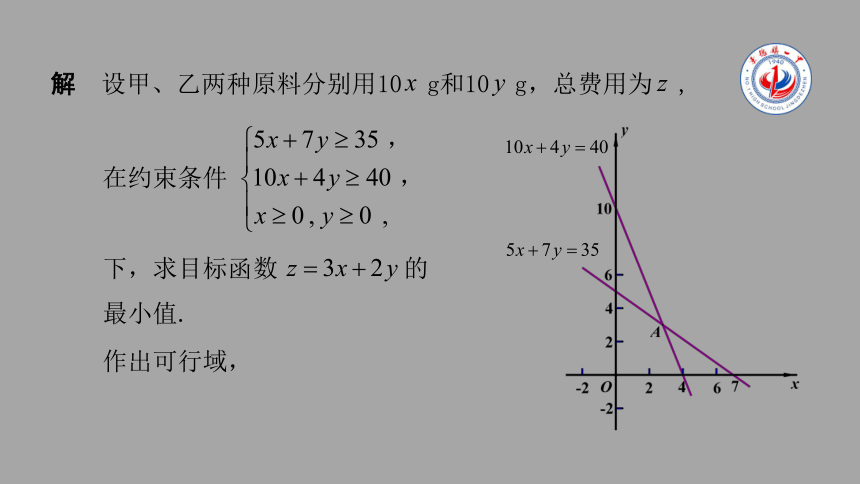
作出可行域,
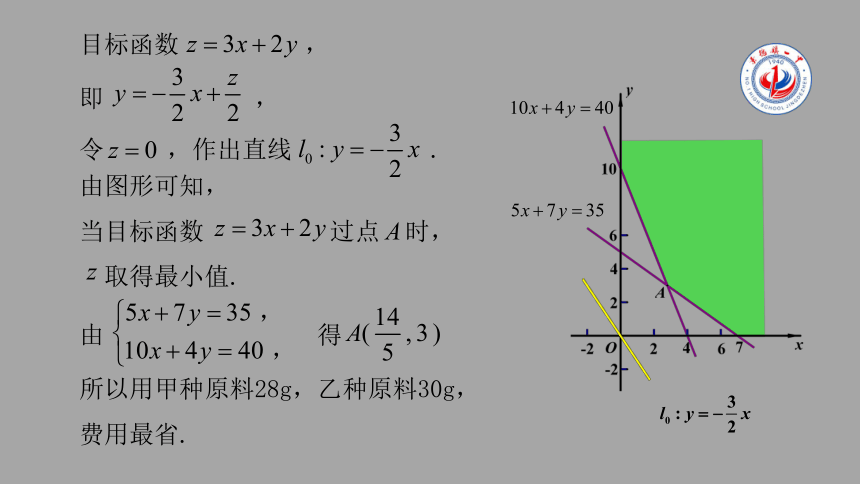
所以用甲种原料28g,乙种原料30g,费用最省.
分析 净收益=售出产品的收入―生产费用
生产费用包括三个部分:
产品成本、污水处理费、交给环保部门的排污费.
(1)售出产品的收入为 ;
(2)产品成本为 ;
(3)污水产生量为 ,污水处理量为 ,
污水处理费为 ;
(4)污水未处理率为1―85%=0.15,所以污水处理站处理后的污水排放量为 ,环保部门要征收的排污费为 ;
所以,每小时净收益
需要考虑的约束条件有:
(1)污水处理站的处理能力有限,即 ;
(2)允许排入河流的污水量有限,即 ;
(3)变量的实际意义,即 , ;
由约束条件,作出可行域,
解答线性规划实际应用题的步骤
(1)化成数学问题:正确理解题意,有时可以借助表格或流程图. 选取恰当的变量,将文字语言转化为数学语言,明确有哪些约束条件,找准目标函数.
(2)求解数学问题:求解线性规划问题。画图对解决线性规划问题至关重要,关键步骤基本上是在图上完成的,所以作图应尽可能准确,图上操作尽可能规范,同时应注意结合变量的实际意义,找到最优解.
(3)回到实际问题:将求解出来的结论反馈到具体的实例中,对问题作出回答.
练 习
练 习
课本第109页 题 2
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修5 第三章 不等式 §4.3 简单线性规划的应用
复习引入
解析答案
反思与感悟
例1 医院用甲、乙两种原料为手术后的病人配营养餐,甲种原料每10g含5单位蛋白质和10单位铁质,售价3元;乙种原料每10g含7单位蛋白质和4单位铁质,售价2元. 若病人每餐至少需要35单位蛋白质和40单位铁质. 试问:应如何使用甲、乙原料,才能既满足营养,又使费用最省?
解析答案
反思与感悟
分析 甲、乙两种原料每10g的数据
作出可行域,
所以用甲种原料28g,乙种原料30g,费用最省.
分析 净收益=售出产品的收入―生产费用
生产费用包括三个部分:
产品成本、污水处理费、交给环保部门的排污费.
(1)售出产品的收入为 ;
(2)产品成本为 ;
(3)污水产生量为 ,污水处理量为 ,
污水处理费为 ;
(4)污水未处理率为1―85%=0.15,所以污水处理站处理后的污水排放量为 ,环保部门要征收的排污费为 ;
所以,每小时净收益
需要考虑的约束条件有:
(1)污水处理站的处理能力有限,即 ;
(2)允许排入河流的污水量有限,即 ;
(3)变量的实际意义,即 , ;
由约束条件,作出可行域,
解答线性规划实际应用题的步骤
(1)化成数学问题:正确理解题意,有时可以借助表格或流程图. 选取恰当的变量,将文字语言转化为数学语言,明确有哪些约束条件,找准目标函数.
(2)求解数学问题:求解线性规划问题。画图对解决线性规划问题至关重要,关键步骤基本上是在图上完成的,所以作图应尽可能准确,图上操作尽可能规范,同时应注意结合变量的实际意义,找到最优解.
(3)回到实际问题:将求解出来的结论反馈到具体的实例中,对问题作出回答.
练 习
练 习
课本第109页 题 2
