北师大版高中数学选修1-1《导数及其应用复习》(1)课件(共25张PPT)
文档属性
| 名称 | 北师大版高中数学选修1-1《导数及其应用复习》(1)课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:51:52 | ||
图片预览







文档简介
(共23张PPT)
导数及其应用复习(1)
在
线
堂
课
北师大版-高中数学选修1-1 第三章 第四章
赣
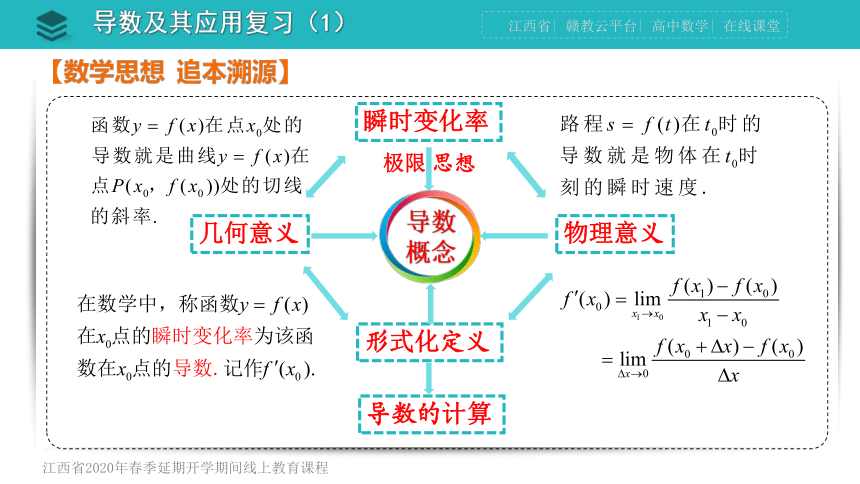
导数概念
瞬时变化率
形式化定义
物理意义
几何意义
极限 思想
【数学思想 追本溯源】
导数的计算
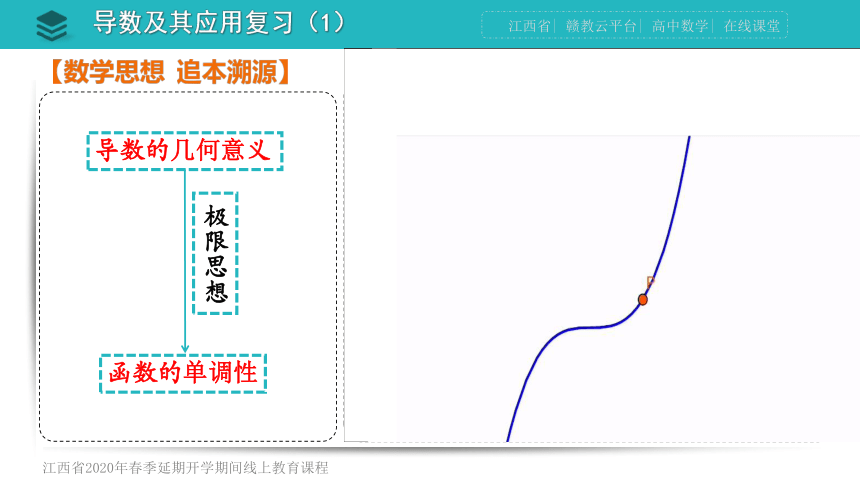
导数的几何意义
函数的单调性
极限思想
【数学思想 追本溯源】
导数的应用
函数的单调性
实际问题中导数的意义
实际生活中的优化问题
函数的极值与最值
函数的零点
函数的图像
在数学问题中的应用
极限思想
数形结合
极限思想
转化思想
【数学思想 追本溯源】
在实际问题中的应用
导数
导数的概念
导数的计算
导数的应用
形式化定义
物理意义
几何意义
定义求导
公式求导
四则运算
在数学问题中的应用
在实际问题中的应用
导数与函数的单调性问题
用导数求函数 单调区间的步骤
函数的单调区间
导函数的图像
导函数在区间的正负性
思考:导函数含参数怎么办?
分类讨论思想
【导数与函数的单调性】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
导函数的一次项系数=0
先看定义域
求导,找出导函数
确定参数分类
讨论的临界值
分析导函数的零点
画出导函数的图像
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
比较所需函数的零点与定义域区间端点值
确定参数分类
讨论的临界值
分析所需函数的零点
画出所需函数的图像
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类
讨论的临界值
分析所需函数的零点
画出所需函数的图像
比较所需函数的零点与定义域区间端点值
例3
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
1.所需函数的一次项系数=0
2.比较所需函数的零点与定义域区间端点值
②
①
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
③
例3
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例3
②
①
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
观察下列函数的图像:
共同点:
1.定义域内单调性明确;
2.函数最多有一个零点.
导函数的零点问题
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
例5
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
例5
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
思考:
导数
导数的概念
导数的计算
导数的应用
形式化定义
物理意义
几何意义
定义求导
公式求导
四则运算
在数学问题中的应用
在实际问题中的应用
导数与函数的单调性问题
【课堂小结】
极限思想
数形结合
转化思想
导函数为含参的“一次函数”类型
导数与函数的单调性问题
【课堂小结】
思考:
导函数为含参的“二次函数”类型?
分类讨论思想
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
分析导函数或所需函数的零点
画出导函数或所需函数的图像
1.导函数或所需函数
的一次项系数=0
2.比较导函数或所需函数的
零点与定义域区间端点值
数形结合思想
【课后作业】
【课后作业答案】
谢谢
THANKS
4/14/2020
导数及其应用复习(1)
在
线
堂
课
北师大版-高中数学选修1-1 第三章 第四章
赣
导数概念
瞬时变化率
形式化定义
物理意义
几何意义
极限 思想
【数学思想 追本溯源】
导数的计算
导数的几何意义
函数的单调性
极限思想
【数学思想 追本溯源】
导数的应用
函数的单调性
实际问题中导数的意义
实际生活中的优化问题
函数的极值与最值
函数的零点
函数的图像
在数学问题中的应用
极限思想
数形结合
极限思想
转化思想
【数学思想 追本溯源】
在实际问题中的应用
导数
导数的概念
导数的计算
导数的应用
形式化定义
物理意义
几何意义
定义求导
公式求导
四则运算
在数学问题中的应用
在实际问题中的应用
导数与函数的单调性问题
用导数求函数 单调区间的步骤
函数的单调区间
导函数的图像
导函数在区间的正负性
思考:导函数含参数怎么办?
分类讨论思想
【导数与函数的单调性】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
导函数的一次项系数=0
先看定义域
求导,找出导函数
确定参数分类
讨论的临界值
分析导函数的零点
画出导函数的图像
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例1
【解析】
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
比较所需函数的零点与定义域区间端点值
确定参数分类
讨论的临界值
分析所需函数的零点
画出所需函数的图像
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类
讨论的临界值
分析所需函数的零点
画出所需函数的图像
比较所需函数的零点与定义域区间端点值
例3
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
1.所需函数的一次项系数=0
2.比较所需函数的零点与定义域区间端点值
②
①
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
③
例3
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
例3
②
①
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
观察下列函数的图像:
共同点:
1.定义域内单调性明确;
2.函数最多有一个零点.
导函数的零点问题
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
例5
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
例5
【解析】
【导数与函数的单调性—— 导函数为含参的“一次函数”类型】
导函数的零点问题
思考:
导数
导数的概念
导数的计算
导数的应用
形式化定义
物理意义
几何意义
定义求导
公式求导
四则运算
在数学问题中的应用
在实际问题中的应用
导数与函数的单调性问题
【课堂小结】
极限思想
数形结合
转化思想
导函数为含参的“一次函数”类型
导数与函数的单调性问题
【课堂小结】
思考:
导函数为含参的“二次函数”类型?
分类讨论思想
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
分析导函数或所需函数的零点
画出导函数或所需函数的图像
1.导函数或所需函数
的一次项系数=0
2.比较导函数或所需函数的
零点与定义域区间端点值
数形结合思想
【课后作业】
【课后作业答案】
谢谢
THANKS
4/14/2020
同课章节目录
