北师大版高中数学选修1-1《导数及其应用复习》(2)课件(共21张PPT)
文档属性
| 名称 | 北师大版高中数学选修1-1《导数及其应用复习》(2)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:55:48 | ||
图片预览





文档简介
(共19张PPT)
导数及其应用复习(2)
在
线
堂
课
北师大版-高中数学选修1-1 第三章 第四章
赣
导函数为含参的“一次函数”类型
导数与函数的单调性问题
思考:
导函数为含参的“二次函数”类型?
分类讨论思想
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
分析导函数或所需函数的零点
画出导函数或所需函数的图像
1.导函数或所需函数
的一次项系数=0
2.比较导函数或所需函数的
零点与定义域区间端点值
数形结合思想
【导数与函数的单调性】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例1
【解析】
先看定义域
求导,找出导函数
确定参数分类讨论的临界值
分析导函数的零点
画出导函数的图像
判别式
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例1
【解析】
例2
【解析】
易分解
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出导函数
确定参数分类讨论的临界值
分析导函数的零点
画出导函数的图像
2.判别式 ;
1.导函数的二次项系数=0
3.比较导函数的零点的大小
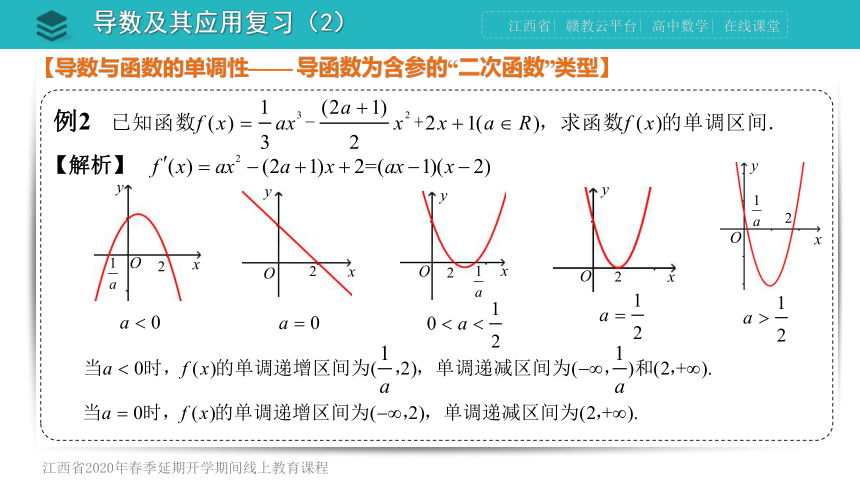
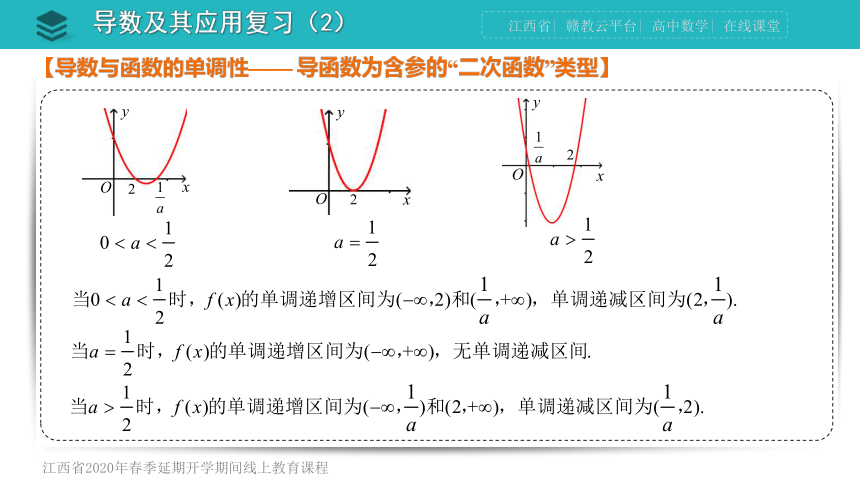
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例2
【解析】
例3
【解析】
不易分解
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
2.判别式 ;
1.所需函数的二次项系数=0
3.比较所需函数的零点的大小
【解析】
例3
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
比较所需函数的零点的大小
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【解析】
例3
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
分析所需函数的零点
比较导函数零点的大小
【方法一】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
①
②
③
【方法二】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
比较导函数零点的大小
①
②
③
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【解析】
例4
1、导函数为含参的“一次函数”类型
2、导函数为含参的“二次函数”类型
分类讨论思想
【课堂小结】
导数与函数的单调性问题
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
画出导函数或所需函数的图像
1.导函数或所需函数的最高次项系数=0
2.分析导函数或所需函数的零点
数形结合思想
【课后作业】
【课后作业答案】
谢谢
THANKS
4/14/2020
导数及其应用复习(2)
在
线
堂
课
北师大版-高中数学选修1-1 第三章 第四章
赣
导函数为含参的“一次函数”类型
导数与函数的单调性问题
思考:
导函数为含参的“二次函数”类型?
分类讨论思想
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
分析导函数或所需函数的零点
画出导函数或所需函数的图像
1.导函数或所需函数
的一次项系数=0
2.比较导函数或所需函数的
零点与定义域区间端点值
数形结合思想
【导数与函数的单调性】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例1
【解析】
先看定义域
求导,找出导函数
确定参数分类讨论的临界值
分析导函数的零点
画出导函数的图像
判别式
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例1
【解析】
例2
【解析】
易分解
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出导函数
确定参数分类讨论的临界值
分析导函数的零点
画出导函数的图像
2.判别式 ;
1.导函数的二次项系数=0
3.比较导函数的零点的大小
例2
【解析】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
例2
【解析】
例3
【解析】
不易分解
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
2.判别式 ;
1.所需函数的二次项系数=0
3.比较所需函数的零点的大小
【解析】
例3
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
比较所需函数的零点的大小
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【解析】
例3
例4
【解析】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
先看定义域
求导,找出所需函数
确定参数分类讨论的临界值
分析所需函数的零点
画出所需函数的图像
分析所需函数的零点
比较导函数零点的大小
【方法一】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
①
②
③
【方法二】
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
比较导函数零点的大小
①
②
③
【导数与函数的单调性—— 导函数为含参的“二次函数”类型】
【解析】
例4
1、导函数为含参的“一次函数”类型
2、导函数为含参的“二次函数”类型
分类讨论思想
【课堂小结】
导数与函数的单调性问题
先看定义域
求导,找出导函数或所需函数
确定参数分类讨论的临界值
画出导函数或所需函数的图像
1.导函数或所需函数的最高次项系数=0
2.分析导函数或所需函数的零点
数形结合思想
【课后作业】
【课后作业答案】
谢谢
THANKS
4/14/2020
同课章节目录
