北师大版高中数学选修1-1第4章《导数应用》复习小结课件(共18张PPT)
文档属性
| 名称 | 北师大版高中数学选修1-1第4章《导数应用》复习小结课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-16 08:55:17 | ||
图片预览





文档简介
(共16张PPT)
《导数应用》复习小结
在
线
堂
课
北师大版-高中数学选修1-1-第4章:导数应用
赣
复习回顾-导数与函数的单调性
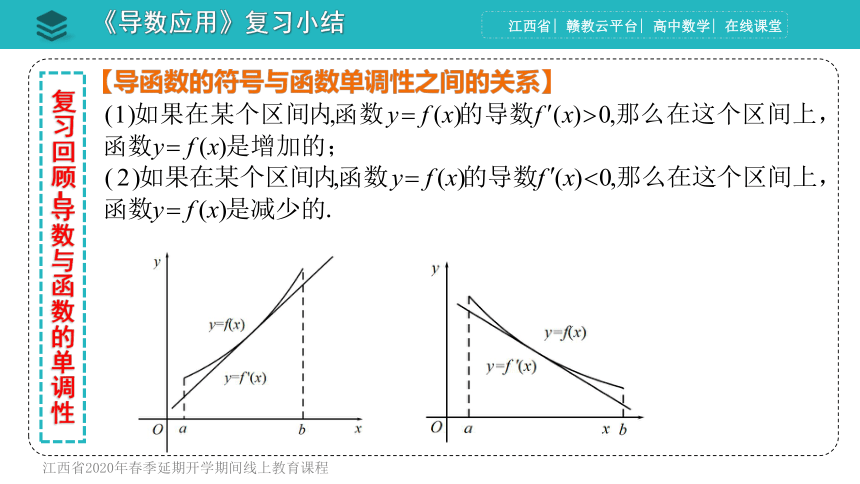
【导函数的符号与函数单调性之间的关系】
【解析】
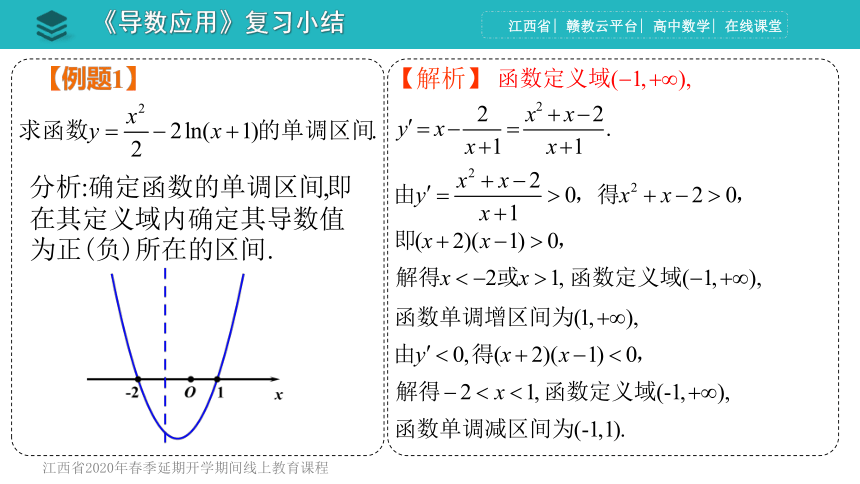
【例题1】
【解析】
1.不等式恒成立问题
2.化归与转化
D
【例题2】
复习回顾-函数的极值
【极值与极值点的概念】
一般情况下,我们可以通过如下步骤求函数y=f (x)的极值点:
1.求出函数f(x)的定义域,求出导函数f ′(x).
2.解方程f ′(x)=0.
3.对于方程f ′(x)=0的每一个解x0 , 分析 f ′(x)在x0左、右两侧的符号
(即f (x)的单调性) , 确定极值点:
(1)若f ′(x)在x0两侧的符号“左正右负” , 则x0为极大值点;
(2)若f ′(x)在x0两侧的符号“左负右正” , 则x0为极小值点;
(3)若f ′(x)在x0两侧的符号相同 , 则x0不是极值点.
【求极值点的步骤】
复习回顾-函数的最值
【最值与最值点的概念】
设函数f(x) 定义域是[a,b],在(a,b)内可导,
①求y=f(x)在(a,b)内的极值(极大值与极小值);
②将函数y=f(x)的各极值与端点值f(a) , f(b)作比较, 其中最大的一
个为最大值,最小的一个为最小值.
(1)函数的极值是在局部范围内讨论,是一个局部概念,而函数的最值是
对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念;
(2)连续不断的函数在闭区间上的最大值(最小值)只有一个,而极值则
可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
复习回顾-函数的最值
【求最值的步骤】
D
【例题3】
1.识图:读懂导函数图像
2.作图:作出原函数的大致图像
3.导函数的正负性与单调性的关系
4.最值与区间的关系
【解析】
【例题4】
【例题4】
1.含参单调区间求解
2.分类讨论
3.含参恒成立问题
4.参数分离,转化为最值
5.化归与转化
课堂小结,提炼升华
2. 不等式恒成立问题的转化
1.求单调区间时注意定义域
3.导函数的符号决定原函数的对应区间的单调性
4.数形结合、化归与转化
【课后作业】
【课后作业参考简析】
【课后作业参考简析】
谢谢
THANKS
4/14/2020
《导数应用》复习小结
在
线
堂
课
北师大版-高中数学选修1-1-第4章:导数应用
赣
复习回顾-导数与函数的单调性
【导函数的符号与函数单调性之间的关系】
【解析】
【例题1】
【解析】
1.不等式恒成立问题
2.化归与转化
D
【例题2】
复习回顾-函数的极值
【极值与极值点的概念】
一般情况下,我们可以通过如下步骤求函数y=f (x)的极值点:
1.求出函数f(x)的定义域,求出导函数f ′(x).
2.解方程f ′(x)=0.
3.对于方程f ′(x)=0的每一个解x0 , 分析 f ′(x)在x0左、右两侧的符号
(即f (x)的单调性) , 确定极值点:
(1)若f ′(x)在x0两侧的符号“左正右负” , 则x0为极大值点;
(2)若f ′(x)在x0两侧的符号“左负右正” , 则x0为极小值点;
(3)若f ′(x)在x0两侧的符号相同 , 则x0不是极值点.
【求极值点的步骤】
复习回顾-函数的最值
【最值与最值点的概念】
设函数f(x) 定义域是[a,b],在(a,b)内可导,
①求y=f(x)在(a,b)内的极值(极大值与极小值);
②将函数y=f(x)的各极值与端点值f(a) , f(b)作比较, 其中最大的一
个为最大值,最小的一个为最小值.
(1)函数的极值是在局部范围内讨论,是一个局部概念,而函数的最值是
对整个定义域而言,是在整体范围内讨论问题,是一个整体性的概念;
(2)连续不断的函数在闭区间上的最大值(最小值)只有一个,而极值则
可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值).
复习回顾-函数的最值
【求最值的步骤】
D
【例题3】
1.识图:读懂导函数图像
2.作图:作出原函数的大致图像
3.导函数的正负性与单调性的关系
4.最值与区间的关系
【解析】
【例题4】
【例题4】
1.含参单调区间求解
2.分类讨论
3.含参恒成立问题
4.参数分离,转化为最值
5.化归与转化
课堂小结,提炼升华
2. 不等式恒成立问题的转化
1.求单调区间时注意定义域
3.导函数的符号决定原函数的对应区间的单调性
4.数形结合、化归与转化
【课后作业】
【课后作业参考简析】
【课后作业参考简析】
谢谢
THANKS
4/14/2020
同课章节目录
