北师大版数学七年级下册4.2图形的全等同步测试(附答案)
文档属性
| 名称 | 北师大版数学七年级下册4.2图形的全等同步测试(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 121.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:19:17 | ||
图片预览


文档简介
一、选择题
1、下列四个几何体中,从上面、左面与正面看到的图形是全等图形的几何体是( )
A.球 B.圆柱
C.三棱柱 D.圆锥
2、已知,如图,△ABC≌△DEF,则图中相等线段的对数是( )
A.3对
B.4对
C.5对
D.6对
3、已知△ABC≌△A′C′B′,∠B与∠C′,∠C与∠B′是对应角,有下列4个结论:①BC=C′B′;②AC=A′B′;③AB=A′B′;④∠ACB=∠A′B′C′,其中正确的结论有( )
A.1个 B.2个
C.3个 D.4个
4、对于两个图形,给出下列说法:①两个图形的周长相等;②两个图形的面积相等;③两个图形的周长和面积都相等;④两个图形的形状相同,大小也相等.其中能得到这两个图形全等的说法共有?( )
A.1个 ????B.2个 ????
C.3个 ????D.4个
5、如右图,如果△ABC和△CDA是全等三角形,那么一定是一组对应边的是?( )
A.AB和CD ????B.AC和AC
C.AD和CB ????D.AD和DC
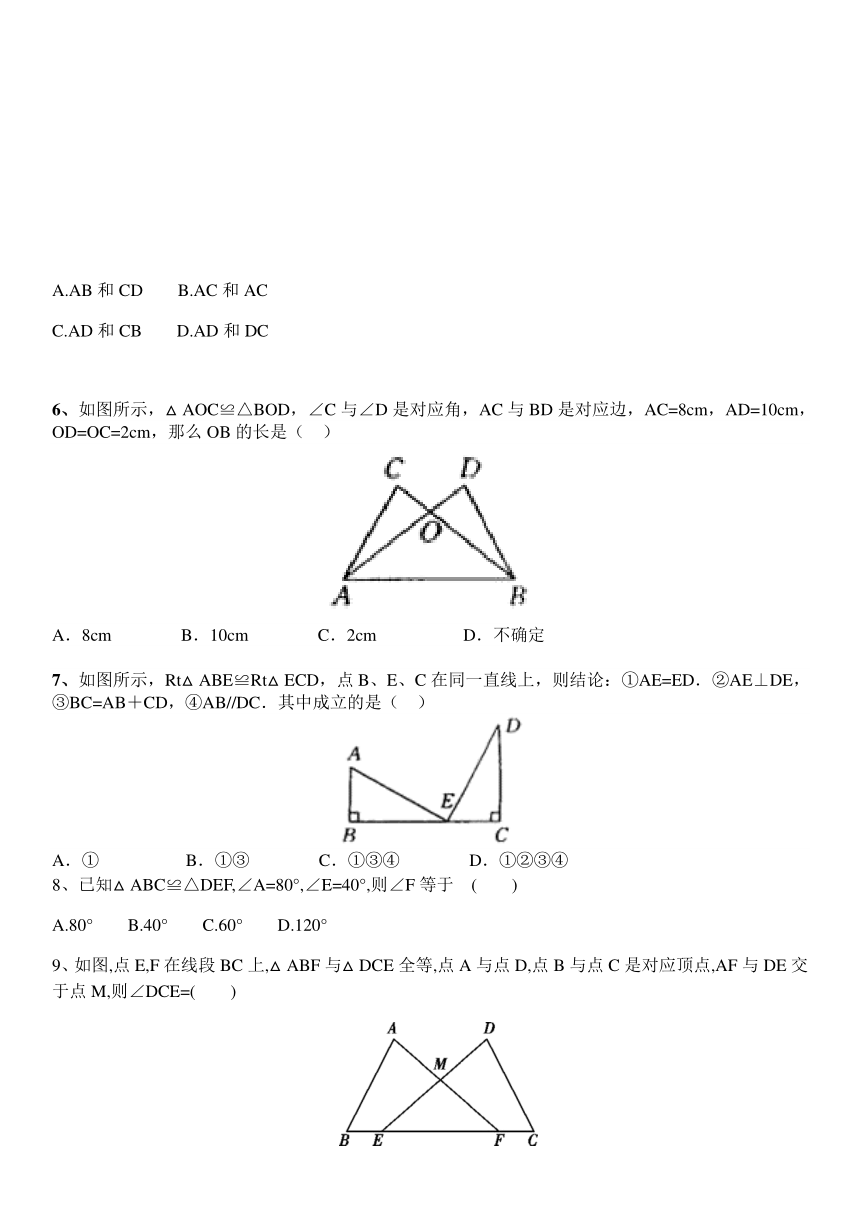
6、如图所示,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,那么OB的长是( )
A.8cm B.10cm C.2cm D.不确定
7、如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED.②AE⊥DE,③BC=AB+CD,④AB//DC.其中成立的是( )
A.① B.①③ C.①③④ D.①②③④
8、已知△ABC≌△DEF,∠A=80°,∠E=40°,则∠F等于?( )
A.80° ????B.40° ????C.60° ????D.120°
9、如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=( )
?
A. ∠B ?? ??B.∠A ???? C.∠EMF ????D.∠AFB
2、填空题
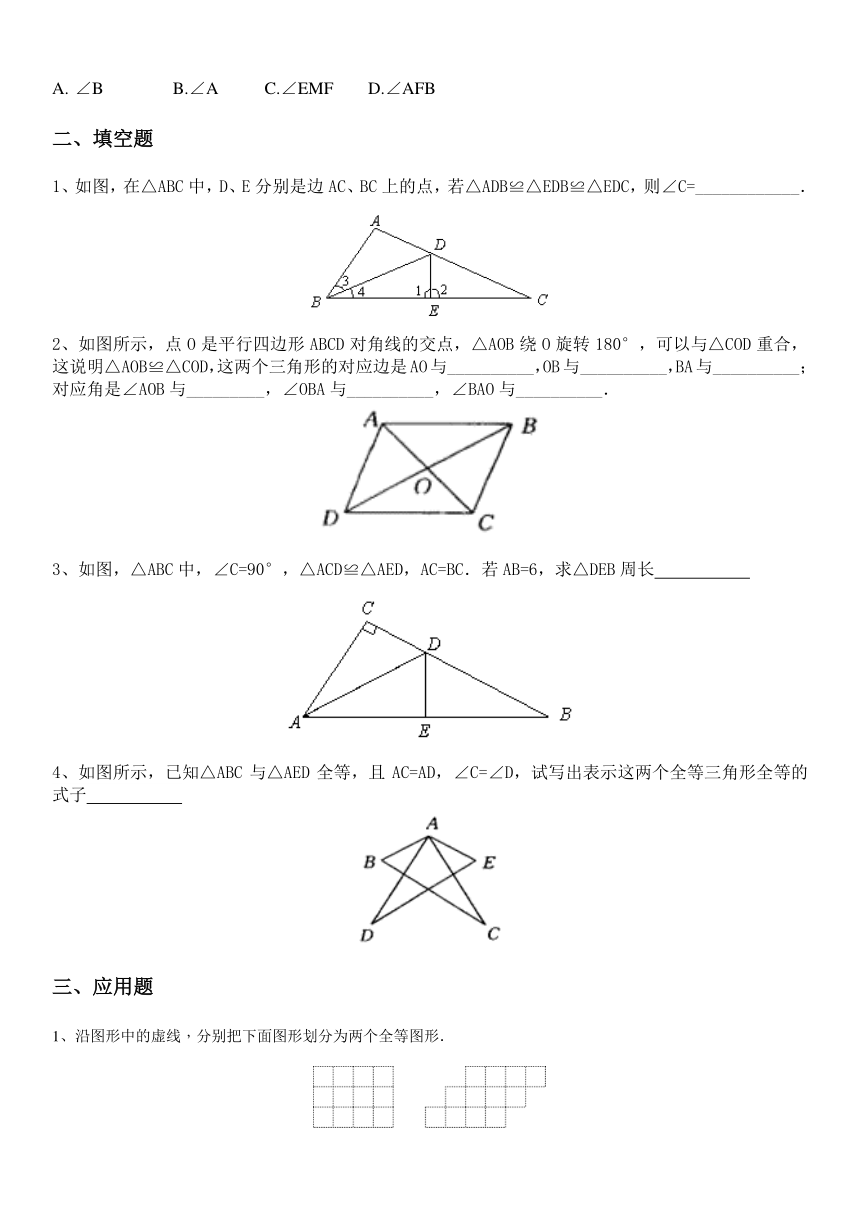
1、如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C=____________.
2、如图所示,点O是平行四边形ABCD对角线的交点,△AOB绕O旋转180°,可以与△COD重合,这说明△AOB≌△COD,这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与_________,∠OBA与__________,∠BAO与__________.
3、如图,△ABC中,∠C=90°,△ACD≌△AED,AC=BC.若AB=6,求△DEB周长
4、如图所示,已知△ABC与△AED全等,且AC=AD,∠C=∠D,试写出表示这两个全等三角形全等的式子
三、应用题
1、沿图形中的虚线,分别把下面图形划分为两个全等图形.
2、已知△DEF≌△MNP,∠D=48°,∠E=52°,MN=12,求∠P的度数和DE的长.
3、如图所示,BE⊥AC,CD⊥AB,垂足分别为E,D,若△ABE≌△ACD,则AE=CD成立吗?为什么?若不成立,你能找出相等的线段吗?
4、如图,△ADC≌△BFE,AB=7,DF=3,求AF的长.
5、如图,已知Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.∠ACE=90°吗?为什么?
6、如图,已知△ABC≌△A′B′C′.求证:
(1)AB//A′B′,AC//A′C′;
(2)BB′=CC′.
参考答案
1、选择题:
1、A
2、B
3、C
4、A
5、B
6、A
7、D
8、C
二、填空题
1、30°
2、CO;OD;DC;
∠COD;∠ODC;∠DCO
3、6
4、△ABC≌△AED
三、应用题:
1、解:如图所示:
或
2、解:因为△DEF≌△MNP,
所以∠P=∠F=180 °-48 °-52 °=80 °,
DE=MN=12.
3、解:不成立,因为它们不是对应边.
可找出的相等线段有AB=AC,AE=AD,BE=CD,DB=EC.
4、解:因为△ADC≌△BFE,
所以AD=BF.
所以AD-DF=BF-DF,
即AF=BD.
又因为AF+BD=AB-DF=7-3=4,
所以AF=BD=2.
5、解:∠ACE=90°成立.
理由:因为Rt△ABC≌Rt△CDE,
所以∠BAC=∠DCE.
因为∠BAC+∠BCA=90 °,
所以∠DCE+∠BCA=90 °.
所以∠ACE=180 °-(∠DCE+∠BCA)=90 °.
6、(1) △ABC≌△A′B′C′,
∴∠B=∠A′B′C′
∠ACB=∠C′,
∴AB//A′B′
AC//A′C′.
(2) ∵△ABC≌△A′B′C′
∴BC=B′C′,
∴BC-B′C=B′C′-B′C,
∴BB′=CC′
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
