沪科版七下数学8.1同底数幂的除法 教学课件(23张PPT)
文档属性
| 名称 | 沪科版七下数学8.1同底数幂的除法 教学课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:40:26 | ||
图片预览







文档简介
(共23张PPT)
8.1 幂的运算
同底数幂的除法
第8章 整式的乘法与因式分解
1
课堂讲解
同底数幂的除法法则
同底数幂的除法法则的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
一个2GB(2GB=221KB)的
便携式U盘可以存储的数码照
片张数与数码照片文件的大小
有关,文件越大,存储的张数
越少.若每张数码照片文件的大
小为211KB,则这个U盘能存储
多少张照片?
1
知识点
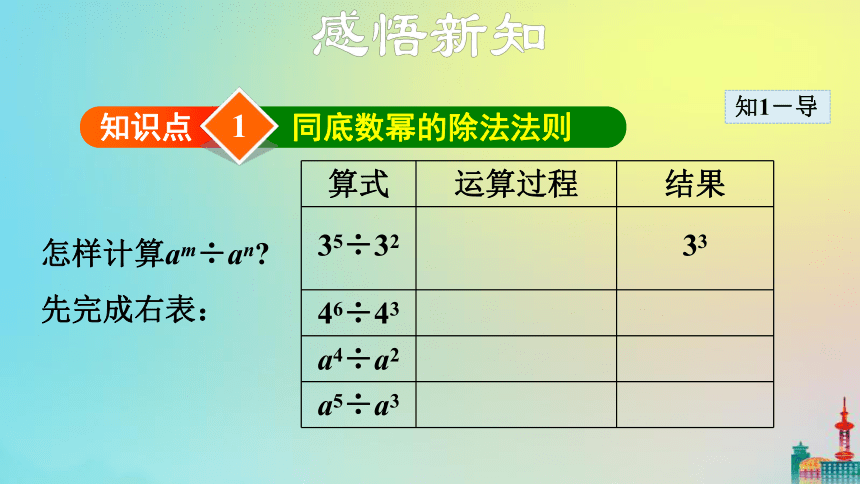
同底数幂的除法法则
怎样计算am÷an?
先完成右表:
算式 运算过程 结果
35÷32
33
46÷43
a4÷a2
a5÷a3
观察上表,发现幂的乘方有什么规律?
一般地,如果字母m,n都是正整数,那么
am÷an =___________________
=___________________.
1. 同底数幂的除法法则:
同底数幂相除,底数不变,指数相减.
即:am÷an=am-n(a≠0,m,n都是正整数,且m>n).
要点精析:
(1)同底数幂除法与同底数幂乘法是互逆运算.
(2)运用此性质时,必须明确底数是什么,指数是什么.
(3)在运算时注意运算顺序,即有多个同底数幂相除时,
先算前两个,然后依次往后算.
(4)同底数幂相除,底数不变,指数相减,而不是相除.
计算:(1)(-x)6÷(-x)3;(2)(x-y)5÷(y-x)2.
例1
解:
(1)原式=(-x)6-3=(-x)3=-x3.
(2)原式=(x-y)5÷(x-y)2=(x-y)5-2=(x-y)3.
导引:
将相同底数的幂直接利用同底数幂除法法则计算,把不同底数的幂化成相同底数幂,再利用同底数幂除法法则计算可得结果.
在(2)中运用整体思想解题.从整体来看以上各题都为同底数幂或可化为同底数幂的运算,在运算时要注意结构和符号.
(1)a5÷a4·a2=a5-4·a2=a3.
(2)(-x)7÷x2=(-x)7÷(-x)2= (-x)7-2=-x5.
(3)(ab)5÷(ab)2=(ab)5-2=(ab)3=a3b3.
(4)(a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2.
例2
计算:
(1)a5÷a4·a2. (2)(-x)7÷x2.
(3)(ab)5÷(ab)2. (4)(a+b)6÷(a+b)4.
解:
1
计算(-x)3 ÷(-x)2等于( )
A.-x B.x
C.-x5 D. x5
(中考·桂林)下列计算正确的是( )
A.(a5)2=a10 B.x16÷x4=x4
C.2a2+3a2=6a4 D.b3·b3=2b3
2
A
A
如果将a8写成下列各式,正确的共有( )
①a4+a4;②(a2)4;③a16÷a2;④(a4)2;
⑤(a4)4;⑥a4·a4;⑦a20÷a12;⑧2a8-a8.
A.3个 B.4个 C.5个 D.6个
3
C
4
计算an+1·an-1÷(an)2(a≠0)的结果是( )
A.1 B.0
C.-1 D.±1
A
2
知识点
同底数幂的除法法则的应用
已知xm=9,xn=27,求x3m-2n的值.
例3
解:
x3m-2n=x3m÷x2n=(xm)3÷(xn)2=93÷272=1.
导引:
x3m-2n=x3m÷x2n=(xm)3÷(xn)2,把已知条件代入即可求值.
此题运用了转化思想,当幂的指数是含有字母的加法时,考虑转化为同底数幂的乘法;当幂的指数是含有字母的减法时,通常转化为同底数幂的除法运算,然后逆用幂的乘方性质并整体代入求值.
计算:(1)[(a2)5·(-a2)3]÷(-a4)3;
(2)(a-b)3÷(b-a)2+(-a-b)5÷(a+b)4.
例4
导引:
有同底数幂的乘除和乘方时,按顺序先乘方再乘除;若底数不同时,要先化为相同底数,再按运算顺序进行计算.
解:
(1)原式=[a10·(-a6)]÷(-a12)=-a16÷(-a12)
=a16-12=a4.
(2)原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4
=(a-b)-(a+b)=a-b-a-b=-2b.
从结构上看,这是两个混合运算,只要注意其结构特征,并按运算顺序和法则去计算即可.注意在运算过程中,一定要先确定符号.
下列计算正确的有( )
①(-c)4÷(-c)2=-c2; ② x6÷x2=x3;
③ a3÷a=a3; ④x10÷(x4÷x2)=x8;
⑤ x2n÷xn-2=xn+2.
A.2个 B.3个
C.4个 D.5个
1
A
2
若7x=m,7y=n,则7x-y等于( )
A.m+n B.m-n
C.mn D.
(中考·湖州)已知xa=3,xb=5,则x4a-3b=( )
A.-44 B.
C. D.
3
D
D
1. 利用同底数幂的除法法则进行计算时,要把底数看清楚,必须是同底,否则需要适当的转化,化为相同的底数.
2. 底数可以是单项式,也可以是多项式,计算时把它看成一个整体;对于三个或三个以上的同底数幂的除法,法则同样适用.
3. 同底数幂的除法法则可以逆用,am-n=am÷an(a≠0,m,n都是正整数,且m>n).
4. 运用同底数幂的除法法则的条件:
(1)运用范围:两个幂的底数相同,且是相除关系,
被除式的指数大于或等于除式的指数,且底数不
能为0.
(2)底数可以是单项式,也可以是多项式.
(3)对于三个或三个以上的同底数幂相除,该法则仍
然成立.
1. 必做:完成教材P50-P51练习T1-T2,
完成教材P54习题8.1T4
8.1 幂的运算
同底数幂的除法
第8章 整式的乘法与因式分解
1
课堂讲解
同底数幂的除法法则
同底数幂的除法法则的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
一个2GB(2GB=221KB)的
便携式U盘可以存储的数码照
片张数与数码照片文件的大小
有关,文件越大,存储的张数
越少.若每张数码照片文件的大
小为211KB,则这个U盘能存储
多少张照片?
1
知识点
同底数幂的除法法则
怎样计算am÷an?
先完成右表:
算式 运算过程 结果
35÷32
33
46÷43
a4÷a2
a5÷a3
观察上表,发现幂的乘方有什么规律?
一般地,如果字母m,n都是正整数,那么
am÷an =___________________
=___________________.
1. 同底数幂的除法法则:
同底数幂相除,底数不变,指数相减.
即:am÷an=am-n(a≠0,m,n都是正整数,且m>n).
要点精析:
(1)同底数幂除法与同底数幂乘法是互逆运算.
(2)运用此性质时,必须明确底数是什么,指数是什么.
(3)在运算时注意运算顺序,即有多个同底数幂相除时,
先算前两个,然后依次往后算.
(4)同底数幂相除,底数不变,指数相减,而不是相除.
计算:(1)(-x)6÷(-x)3;(2)(x-y)5÷(y-x)2.
例1
解:
(1)原式=(-x)6-3=(-x)3=-x3.
(2)原式=(x-y)5÷(x-y)2=(x-y)5-2=(x-y)3.
导引:
将相同底数的幂直接利用同底数幂除法法则计算,把不同底数的幂化成相同底数幂,再利用同底数幂除法法则计算可得结果.
在(2)中运用整体思想解题.从整体来看以上各题都为同底数幂或可化为同底数幂的运算,在运算时要注意结构和符号.
(1)a5÷a4·a2=a5-4·a2=a3.
(2)(-x)7÷x2=(-x)7÷(-x)2= (-x)7-2=-x5.
(3)(ab)5÷(ab)2=(ab)5-2=(ab)3=a3b3.
(4)(a+b)6÷(a+b)4=(a+b)6-4=(a+b)2=a2+2ab+b2.
例2
计算:
(1)a5÷a4·a2. (2)(-x)7÷x2.
(3)(ab)5÷(ab)2. (4)(a+b)6÷(a+b)4.
解:
1
计算(-x)3 ÷(-x)2等于( )
A.-x B.x
C.-x5 D. x5
(中考·桂林)下列计算正确的是( )
A.(a5)2=a10 B.x16÷x4=x4
C.2a2+3a2=6a4 D.b3·b3=2b3
2
A
A
如果将a8写成下列各式,正确的共有( )
①a4+a4;②(a2)4;③a16÷a2;④(a4)2;
⑤(a4)4;⑥a4·a4;⑦a20÷a12;⑧2a8-a8.
A.3个 B.4个 C.5个 D.6个
3
C
4
计算an+1·an-1÷(an)2(a≠0)的结果是( )
A.1 B.0
C.-1 D.±1
A
2
知识点
同底数幂的除法法则的应用
已知xm=9,xn=27,求x3m-2n的值.
例3
解:
x3m-2n=x3m÷x2n=(xm)3÷(xn)2=93÷272=1.
导引:
x3m-2n=x3m÷x2n=(xm)3÷(xn)2,把已知条件代入即可求值.
此题运用了转化思想,当幂的指数是含有字母的加法时,考虑转化为同底数幂的乘法;当幂的指数是含有字母的减法时,通常转化为同底数幂的除法运算,然后逆用幂的乘方性质并整体代入求值.
计算:(1)[(a2)5·(-a2)3]÷(-a4)3;
(2)(a-b)3÷(b-a)2+(-a-b)5÷(a+b)4.
例4
导引:
有同底数幂的乘除和乘方时,按顺序先乘方再乘除;若底数不同时,要先化为相同底数,再按运算顺序进行计算.
解:
(1)原式=[a10·(-a6)]÷(-a12)=-a16÷(-a12)
=a16-12=a4.
(2)原式=(a-b)3÷(a-b)2-(a+b)5÷(a+b)4
=(a-b)-(a+b)=a-b-a-b=-2b.
从结构上看,这是两个混合运算,只要注意其结构特征,并按运算顺序和法则去计算即可.注意在运算过程中,一定要先确定符号.
下列计算正确的有( )
①(-c)4÷(-c)2=-c2; ② x6÷x2=x3;
③ a3÷a=a3; ④x10÷(x4÷x2)=x8;
⑤ x2n÷xn-2=xn+2.
A.2个 B.3个
C.4个 D.5个
1
A
2
若7x=m,7y=n,则7x-y等于( )
A.m+n B.m-n
C.mn D.
(中考·湖州)已知xa=3,xb=5,则x4a-3b=( )
A.-44 B.
C. D.
3
D
D
1. 利用同底数幂的除法法则进行计算时,要把底数看清楚,必须是同底,否则需要适当的转化,化为相同的底数.
2. 底数可以是单项式,也可以是多项式,计算时把它看成一个整体;对于三个或三个以上的同底数幂的除法,法则同样适用.
3. 同底数幂的除法法则可以逆用,am-n=am÷an(a≠0,m,n都是正整数,且m>n).
4. 运用同底数幂的除法法则的条件:
(1)运用范围:两个幂的底数相同,且是相除关系,
被除式的指数大于或等于除式的指数,且底数不
能为0.
(2)底数可以是单项式,也可以是多项式.
(3)对于三个或三个以上的同底数幂相除,该法则仍
然成立.
1. 必做:完成教材P50-P51练习T1-T2,
完成教材P54习题8.1T4
