沪科版七下数学8.2 单项式与多项式相乘 教学课件(26张PPT)
文档属性
| 名称 | 沪科版七下数学8.2 单项式与多项式相乘 教学课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 968.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:49:45 | ||
图片预览






文档简介
(共26张PPT)
8.2 整式乘法
单项式与多项式相乘
第8章 整式的乘法与因式分解
1
课堂讲解
单项式与多项式相乘的法则
单项式与多项式相乘法则的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
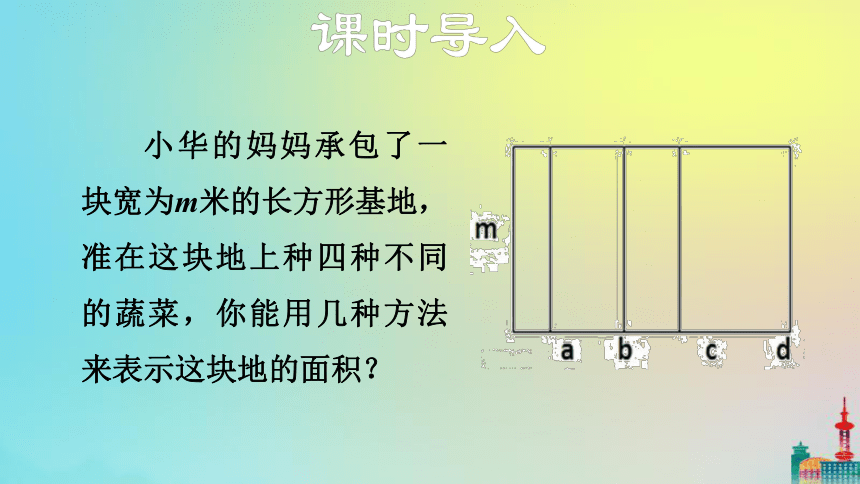
小华的妈妈承包了一块宽为m米的长方形基地,准在这块地上种四种不同的蔬菜,你能用几种方法来表示这块地的面积?
1
知识点
单项式与多项式相乘的法则
问题
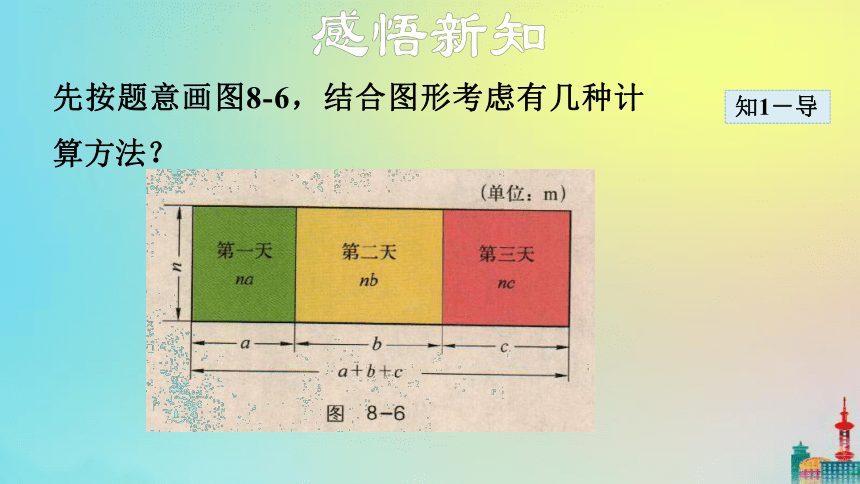
一个施工队修筑一条路面宽为n m的公路,第一天修筑a m长,第二天修筑b m长,第三天修筑c m长,3天修筑路面的面积共是多少?
先按题意画图8-6,结合图形考虑有几种计算方法?
方法一:3天共修筑路面的总长为(a+b+c)m,因为路面的宽为n m,所以3天共修筑路面_______m2.
方法二:先分别计算每天修筑路面的面积,然后相加,则3天共修筑路面_______m2.
因此,有_______________=_______________.
事实上,因为代数式中的字母都表示数,因此,
根据乘法分配律,可得到
n(a+b+c)=(na+nb+nc).
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
要点精析:
(1)单项式与多项式相乘,实质上是利用乘法分配律将其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,必须合并同类项从而得到最简结果.
易错警示:
(1)法则中的每一项,是指含符号的每一项,容易出现符号错误.
(2)运用分配律计算时容易漏乘项,特别是常数项.
计算:
(1)(-2x)(x2-x+1);(2)a(a2+a)-a2(a-2).
例1
(1) (-2x)(x2-x+1)
=(-2x)x2+(-2x)·(-x)+ (-2x)·1
=-2x3+2x2-2x.
解:
(2) a(a2+a)-a2(a-2).
=a·a2 +a·a-a2·a+2a2
=a3+a2-a3+2a2
=3a2.
计算:
(1)-5x(2x2-3x+1);
(2)x2(3-x)-x(-x2-2x+1).
例2
直接根据单项式乘多项式法则进行计算,把“单×多”转化为“单×单”.
导引:
(1)原式=(-5x)·2x2+(-5x)·(-3x)+(-5x)·1
=-10x3+15x2-5x;
(2)原式=3x2-x3+x3+2x2-x
=5x2-x.
解:
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号相连,然后按单项式与单项式相乘的法则逐个计算,特别要注意符号.
1 (中考·湖州)计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1
C.6x3+2x D.6x2+2x
2 化简-x(2-3x)的结果为( )
A.-2x-6x2 B.-2x+6x2
C.-2x-3x2 D.-2x+3x2
C
D
2
知识点
单项式与多项式相乘法则的应用
先化简,再求值:
x2(3-x)+x(x2-2x)+1,其中x=-3.
直接将已知数值代入式子求值运算量较大,一般是先化简,再将数值代入求值.
例3
导引:
原式=3x2-x3+x3-2x2+1
=x2+1.
当x=-3时,原式=(-3)2+1=10.
解:
此题是单项式乘以多项式与加减相结合的混合运算,运算过程中通常是先算乘法,再算加减,其实质就是去括号和合并同类项.
(1) (中考·龙岩)先化简,再求值:
3(2x+1)+2(3-x),其中x=-1.
(2)已知ab2=-1,求(-ab)(a2b5-ab3-b)的值.
例4
(1)原式=6x+3+6-2x=4x+9.
当x=-1时,原式=4×(-1)+9=5.
(2)原式=-a3b6+a2b4+ab2=-(ab2)3+(ab2)2+ab2.
当ab2=-1时,原式=-(-1)3+(-1)2+(-1)=1.
解:
1 今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:
-3xy(4y-2x-1)=-12xy2+6x2y+ , 的地方被钢笔水弄污了,你认为 内应填写( )
A.3xy B.-3xy C.-1 D.1
A
2 要使x(x+a)+3x-2b=x2+5x+4成立,则a、b的值分别为( )
A.a=-2,b=-2
B.a=2,b=2
C.a=2,b=-2
D.a=-2,b=2
C
运用单项式乘多项式的法则时要明确“三点”:
(1)注意符号问题,多项式的每一项都包括其前面的符号,同时注意单项式的符号.
(2)对于混合运算注意运算顺序,先算幂的乘方或积的乘方,再算乘法,最后有同类项的要合并.
(3)单项式与多项式相乘的结果是一个多项式,其项数与因式中多项式的项数相同,可以在运算中检验是否漏了乘某些项.
1. 必做: 完成教材P61练习T1-T3,
习题8.2T4(1)-(3)
8.2 整式乘法
单项式与多项式相乘
第8章 整式的乘法与因式分解
1
课堂讲解
单项式与多项式相乘的法则
单项式与多项式相乘法则的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
小华的妈妈承包了一块宽为m米的长方形基地,准在这块地上种四种不同的蔬菜,你能用几种方法来表示这块地的面积?
1
知识点
单项式与多项式相乘的法则
问题
一个施工队修筑一条路面宽为n m的公路,第一天修筑a m长,第二天修筑b m长,第三天修筑c m长,3天修筑路面的面积共是多少?
先按题意画图8-6,结合图形考虑有几种计算方法?
方法一:3天共修筑路面的总长为(a+b+c)m,因为路面的宽为n m,所以3天共修筑路面_______m2.
方法二:先分别计算每天修筑路面的面积,然后相加,则3天共修筑路面_______m2.
因此,有_______________=_______________.
事实上,因为代数式中的字母都表示数,因此,
根据乘法分配律,可得到
n(a+b+c)=(na+nb+nc).
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.
要点精析:
(1)单项式与多项式相乘,实质上是利用乘法分配律将其转化为单项式乘以单项式的问题.
(2)单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同.
(3)计算过程要注意符号,单项式乘多项式的每一项时,要包括它前面的符号,同时还要注意单项式的符号.
(4)对于混合运算,应注意运算顺序;最后有同类项时,必须合并同类项从而得到最简结果.
易错警示:
(1)法则中的每一项,是指含符号的每一项,容易出现符号错误.
(2)运用分配律计算时容易漏乘项,特别是常数项.
计算:
(1)(-2x)(x2-x+1);(2)a(a2+a)-a2(a-2).
例1
(1) (-2x)(x2-x+1)
=(-2x)x2+(-2x)·(-x)+ (-2x)·1
=-2x3+2x2-2x.
解:
(2) a(a2+a)-a2(a-2).
=a·a2 +a·a-a2·a+2a2
=a3+a2-a3+2a2
=3a2.
计算:
(1)-5x(2x2-3x+1);
(2)x2(3-x)-x(-x2-2x+1).
例2
直接根据单项式乘多项式法则进行计算,把“单×多”转化为“单×单”.
导引:
(1)原式=(-5x)·2x2+(-5x)·(-3x)+(-5x)·1
=-10x3+15x2-5x;
(2)原式=3x2-x3+x3+2x2-x
=5x2-x.
解:
单项式与多项式相乘时,依据法则将其转化为
单项式与单项式相乘,相乘每两项的积用“+”号相连,然后按单项式与单项式相乘的法则逐个计算,特别要注意符号.
1 (中考·湖州)计算2x(3x2+1),正确的结果是( )
A.5x3+2x B.6x3+1
C.6x3+2x D.6x2+2x
2 化简-x(2-3x)的结果为( )
A.-2x-6x2 B.-2x+6x2
C.-2x-3x2 D.-2x+3x2
C
D
2
知识点
单项式与多项式相乘法则的应用
先化简,再求值:
x2(3-x)+x(x2-2x)+1,其中x=-3.
直接将已知数值代入式子求值运算量较大,一般是先化简,再将数值代入求值.
例3
导引:
原式=3x2-x3+x3-2x2+1
=x2+1.
当x=-3时,原式=(-3)2+1=10.
解:
此题是单项式乘以多项式与加减相结合的混合运算,运算过程中通常是先算乘法,再算加减,其实质就是去括号和合并同类项.
(1) (中考·龙岩)先化简,再求值:
3(2x+1)+2(3-x),其中x=-1.
(2)已知ab2=-1,求(-ab)(a2b5-ab3-b)的值.
例4
(1)原式=6x+3+6-2x=4x+9.
当x=-1时,原式=4×(-1)+9=5.
(2)原式=-a3b6+a2b4+ab2=-(ab2)3+(ab2)2+ab2.
当ab2=-1时,原式=-(-1)3+(-1)2+(-1)=1.
解:
1 今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:
-3xy(4y-2x-1)=-12xy2+6x2y+ , 的地方被钢笔水弄污了,你认为 内应填写( )
A.3xy B.-3xy C.-1 D.1
A
2 要使x(x+a)+3x-2b=x2+5x+4成立,则a、b的值分别为( )
A.a=-2,b=-2
B.a=2,b=2
C.a=2,b=-2
D.a=-2,b=2
C
运用单项式乘多项式的法则时要明确“三点”:
(1)注意符号问题,多项式的每一项都包括其前面的符号,同时注意单项式的符号.
(2)对于混合运算注意运算顺序,先算幂的乘方或积的乘方,再算乘法,最后有同类项的要合并.
(3)单项式与多项式相乘的结果是一个多项式,其项数与因式中多项式的项数相同,可以在运算中检验是否漏了乘某些项.
1. 必做: 完成教材P61练习T1-T3,
习题8.2T4(1)-(3)
