沪科版七下数学8.3完全平方公式 教学课件(36张PPT)
文档属性
| 名称 | 沪科版七下数学8.3完全平方公式 教学课件(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 13:52:51 | ||
图片预览











文档简介
(共36张PPT)
8.3 完全平方公式与平方差公式
完全平方公式
第8章 整式的乘法与因式分解
1
课堂讲解
完全平方公式
完全平方公式的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
靠垫是舒适实用的家庭小点缀,一些心灵手巧的人
喜欢自己动手制作靠垫.图中右下角的靠垫面子用5块布
料拼合而成,应用了哪些数学知识?
1
知识点
完全平方公式
问 题 1
由多项式乘法可得乘法公式
(a+b)2=a2+2ab+b2. ①
(a-b)2=a2-2ab+b2. ②
上面两个公式,今后可以直接应用于运算,称为完全平方公式(formula for the square of the sum).
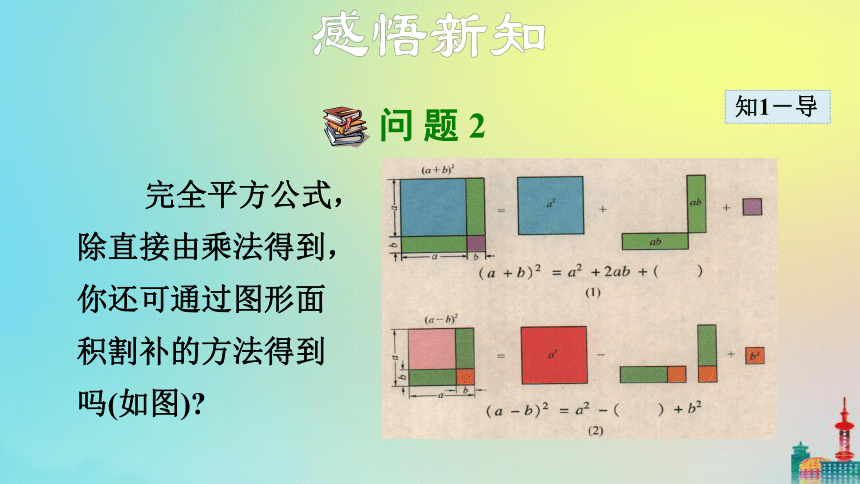
问 题 2
完全平方公式,除直接由乘法得到,你还可通过图形面积割补的方法得到吗(如图)?
这两个公式中的②式也可在①式中用-b代替b而得出.
完全平方公式用语言叙述是:两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
完全平方公式
两个数的和(或差)的平方,等于这两个数的平方和,加(或减)这两个数乘积的2倍.
用式子表示为:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
要点精析:
(1)弄清公式的特征
公式的左边是一个二项式的完全平方,公式的右边是一个三项式,包括左边二项式的各项的平方和,另一项是该两项的乘积的两倍;二项式的差的完全平方公式是和的完全平方公式的特例.
(2)理解字母a,b的意义
公式中的字母a,b,它们可以表示具体的数,也可以表示单项式.
(3)学会用口诀加深记忆
对于公式(a±b)2=a2±2ab+b2,可以用下述简单的口诀来记忆:
头平方和尾平方,
头(乘)尾两倍在中央,
中间符号照原样.
利用乘法公式计算:
(1)(2x+y)2. (2)(3a-2b)2.
例1
运用公式计算,要先识别a,b在具体式子中分别表示什么.
(1)(2x+y)2=(2x)2+2·(2x)y+y2
( a +b)2= a2 + 2 a b+b2
=4x2+4xy+y2.
解:
(2)(3a-2b)2=(3a)2-2·(3a)(2b)+(2b)2
( a - b)2 = a2 - 2 a b + b2.
=9a2-12ab+4b2.
在应用公式(a±b)2=a2±2ab+b2时关键是弄清题目中哪一个相当于公式中的a,哪一个相当于公式中的b,同时还要确定是用两数和的完全平方公式还是两数差的完全平方公式;解(1)(2)题时还用到了互为相反数的两数的平方相等.
计算:
(1)(2x-1)2-(3x+1)2;
(2)(x+y)(-x+y)(x2-y2).
例2
对于(1)可分别利用完全平方公式计算,再合并同类项;对于(2)先利用多项式乘多项式法则计算前两个因式的积,再利用完全平方公式进行计算.
导引:
(1) 原式=4x2-4x+1-(9x2+6x+1)
=4x2-4x+1-9x2-6x-1
=-5x2-10x;
(2)原式=-(x+y)(x-y)(x2-y2)
=-(x2-y2)2
=-(x4-2x2y2+y4)
=-x4+2x2y2-y4.
解:
在解答与乘法公式有关的比较复杂的整式计算问题时,要注意观察题目结构特征,灵活运用多项式乘多项式法则和完全平方公式求解.
1 给多项式4x2+1加上一个单项式,使它成为一个完全平方式,则加上的单项式不可以是( )
A.4x B.-4x
C.4x4 D.-4x4
D
2 若x2+6x+k是完全平方式,则k等于( )
A.9 B.-9
C.±9 D.±3
A
3 计算(-a-b)2等于( )
A.a2+b2 B.a2-b2
C.a2+2ab+b2 D.a2-2ab+b2
C
4 (中考·遵义)下列运算正确的是( )
A.4a-a=3
B.2(2a-b)=4a-b
C.(a+b)2=a2+b2
D.(a+2)(a-2)=a2-4
D
2
知识点
完全平方公式的应用
1. 拓展:
(1) 公式中的字母a,b,还可为多项式表示的数或其他的代数式所表示的数.
(2) 利用完全平方公式,可得到a+b,ab,a-b,a2+b2有下列重要关系:
①a2+b2=(a+b)2-2ab=(a-b)2+2ab;
②(a+b)2-(a-b)2=4ab.
2. 易错警示:易出现形如(a±b)2=a2±b2的错误.为了防止类似错误,要明确以下三点:
(1) 意义不同: (a±b)2表示数a与数b和(差)的平方,而a2±b2表示数a的平方与数b的平方的和(差).
(2) 读法不同: (a±b)2读作a,b两数和(差)的平方;a2±b2读作a,b两数平方的和(差).
(3) 运算顺序不同: (a±b)2是先算a,b两数的和(差),后算和(差)的平方; a2±b2是先算a2与b2,后算a2,b2的和(差).
(1)若(x-5)2=x2+kx+25,则k的取值是多少?
(2)先化简,再求值:
(1+a)(1-a)+(a-2)2,其中a=-3;
(3)已知x2-4x+1=0,
求代数式(2x-3)2-(x+y)(x-y)-y2的值.
例3
对于(1)把左边的式子展开后对比各项,可得解;
对于(2)利用多项式乘多项式法则和完全平方公式展开,合并同类项后代入求值;对于(3)先化简代数式,后将条件变形整体代入求值.
导引:
(1)依题意,得x2-10x+25=x2+kx+25.
所以k=-10.
(2)原式=1-a2+a2-4a+4=-4a+5,
当a=-3时,原式=12+5=17.
解:
(3)原式=4x2-12x+9-x2+y2-y2
=3x2-12x+9=3(x2-4x+3).
因为x2-4x+1=0,所以x2-4x=-1,
所以,原式=3×(-1+3)=6.
本题(3)中运用了整体思想解题.对于涉及乘法公式的求值或求字母的值问题,一般都需要运用乘法公式将原式化简,再对比(如(1))、将字母取值代入(如(2))、将条件变形整体代入(如(3))求值,在(3)中若想通过条件求出字母的值代入求值,将会遇到目前还不会解的一元二次方程而使解题受阻,本解法可使问题变得简单.
一花农有两块正方形茶花苗圃,边长分别为30.1 m,29.5 m,现将这两块苗圃的边长都增加1.5 m.求两块苗圃的面积分别增加了多少平方米.
例4
设原正方形苗圃的边长为a(m),边长增加1.5 m后,
新正方形的 边长为(a+1.5) m.
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25.
解:
当 a=30.1 时,3a+2.25=3×30.1+2.25=92.55;
当 a=29.5 时,3a+2.25=3×29.5+2.25=90.75.
答:两块苗圃的面积分别增加了 92.55 m2,90.75 m2.
在解答实际问题时,利用乘法公式会减少计算量,提高准确性.
1 若(a+b)2=(a-b)2+A,则A为( )
A.2ab B.-2ab
C.4ab D.-4ab
2 若(x+3)2=x2+ax+9,则a的值为( )
A.3 B.±3
C.6 D.±6
C
C
3 如图,图中最大的正方形的面积是( )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
C
1. 完全平方公式的特征:
左边是二项式的平方,右边是二次三项式,其中两项分别是公式左边两项的平方,中间一项是左边二项式中两项乘积的2倍.
2. 公式中的a,b可以是单项式,也可以是多项式.公式也可以逆用:a2±2ab+b2=(a±b)2.
1. 必做: 完成教材P69练习T1-2, 习题8.3T1,T7
8.3 完全平方公式与平方差公式
完全平方公式
第8章 整式的乘法与因式分解
1
课堂讲解
完全平方公式
完全平方公式的应用
2
课时流程
作业提升
逐点
导讲练
课堂小结
靠垫是舒适实用的家庭小点缀,一些心灵手巧的人
喜欢自己动手制作靠垫.图中右下角的靠垫面子用5块布
料拼合而成,应用了哪些数学知识?
1
知识点
完全平方公式
问 题 1
由多项式乘法可得乘法公式
(a+b)2=a2+2ab+b2. ①
(a-b)2=a2-2ab+b2. ②
上面两个公式,今后可以直接应用于运算,称为完全平方公式(formula for the square of the sum).
问 题 2
完全平方公式,除直接由乘法得到,你还可通过图形面积割补的方法得到吗(如图)?
这两个公式中的②式也可在①式中用-b代替b而得出.
完全平方公式用语言叙述是:两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
完全平方公式
两个数的和(或差)的平方,等于这两个数的平方和,加(或减)这两个数乘积的2倍.
用式子表示为:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
要点精析:
(1)弄清公式的特征
公式的左边是一个二项式的完全平方,公式的右边是一个三项式,包括左边二项式的各项的平方和,另一项是该两项的乘积的两倍;二项式的差的完全平方公式是和的完全平方公式的特例.
(2)理解字母a,b的意义
公式中的字母a,b,它们可以表示具体的数,也可以表示单项式.
(3)学会用口诀加深记忆
对于公式(a±b)2=a2±2ab+b2,可以用下述简单的口诀来记忆:
头平方和尾平方,
头(乘)尾两倍在中央,
中间符号照原样.
利用乘法公式计算:
(1)(2x+y)2. (2)(3a-2b)2.
例1
运用公式计算,要先识别a,b在具体式子中分别表示什么.
(1)(2x+y)2=(2x)2+2·(2x)y+y2
( a +b)2= a2 + 2 a b+b2
=4x2+4xy+y2.
解:
(2)(3a-2b)2=(3a)2-2·(3a)(2b)+(2b)2
( a - b)2 = a2 - 2 a b + b2.
=9a2-12ab+4b2.
在应用公式(a±b)2=a2±2ab+b2时关键是弄清题目中哪一个相当于公式中的a,哪一个相当于公式中的b,同时还要确定是用两数和的完全平方公式还是两数差的完全平方公式;解(1)(2)题时还用到了互为相反数的两数的平方相等.
计算:
(1)(2x-1)2-(3x+1)2;
(2)(x+y)(-x+y)(x2-y2).
例2
对于(1)可分别利用完全平方公式计算,再合并同类项;对于(2)先利用多项式乘多项式法则计算前两个因式的积,再利用完全平方公式进行计算.
导引:
(1) 原式=4x2-4x+1-(9x2+6x+1)
=4x2-4x+1-9x2-6x-1
=-5x2-10x;
(2)原式=-(x+y)(x-y)(x2-y2)
=-(x2-y2)2
=-(x4-2x2y2+y4)
=-x4+2x2y2-y4.
解:
在解答与乘法公式有关的比较复杂的整式计算问题时,要注意观察题目结构特征,灵活运用多项式乘多项式法则和完全平方公式求解.
1 给多项式4x2+1加上一个单项式,使它成为一个完全平方式,则加上的单项式不可以是( )
A.4x B.-4x
C.4x4 D.-4x4
D
2 若x2+6x+k是完全平方式,则k等于( )
A.9 B.-9
C.±9 D.±3
A
3 计算(-a-b)2等于( )
A.a2+b2 B.a2-b2
C.a2+2ab+b2 D.a2-2ab+b2
C
4 (中考·遵义)下列运算正确的是( )
A.4a-a=3
B.2(2a-b)=4a-b
C.(a+b)2=a2+b2
D.(a+2)(a-2)=a2-4
D
2
知识点
完全平方公式的应用
1. 拓展:
(1) 公式中的字母a,b,还可为多项式表示的数或其他的代数式所表示的数.
(2) 利用完全平方公式,可得到a+b,ab,a-b,a2+b2有下列重要关系:
①a2+b2=(a+b)2-2ab=(a-b)2+2ab;
②(a+b)2-(a-b)2=4ab.
2. 易错警示:易出现形如(a±b)2=a2±b2的错误.为了防止类似错误,要明确以下三点:
(1) 意义不同: (a±b)2表示数a与数b和(差)的平方,而a2±b2表示数a的平方与数b的平方的和(差).
(2) 读法不同: (a±b)2读作a,b两数和(差)的平方;a2±b2读作a,b两数平方的和(差).
(3) 运算顺序不同: (a±b)2是先算a,b两数的和(差),后算和(差)的平方; a2±b2是先算a2与b2,后算a2,b2的和(差).
(1)若(x-5)2=x2+kx+25,则k的取值是多少?
(2)先化简,再求值:
(1+a)(1-a)+(a-2)2,其中a=-3;
(3)已知x2-4x+1=0,
求代数式(2x-3)2-(x+y)(x-y)-y2的值.
例3
对于(1)把左边的式子展开后对比各项,可得解;
对于(2)利用多项式乘多项式法则和完全平方公式展开,合并同类项后代入求值;对于(3)先化简代数式,后将条件变形整体代入求值.
导引:
(1)依题意,得x2-10x+25=x2+kx+25.
所以k=-10.
(2)原式=1-a2+a2-4a+4=-4a+5,
当a=-3时,原式=12+5=17.
解:
(3)原式=4x2-12x+9-x2+y2-y2
=3x2-12x+9=3(x2-4x+3).
因为x2-4x+1=0,所以x2-4x=-1,
所以,原式=3×(-1+3)=6.
本题(3)中运用了整体思想解题.对于涉及乘法公式的求值或求字母的值问题,一般都需要运用乘法公式将原式化简,再对比(如(1))、将字母取值代入(如(2))、将条件变形整体代入(如(3))求值,在(3)中若想通过条件求出字母的值代入求值,将会遇到目前还不会解的一元二次方程而使解题受阻,本解法可使问题变得简单.
一花农有两块正方形茶花苗圃,边长分别为30.1 m,29.5 m,现将这两块苗圃的边长都增加1.5 m.求两块苗圃的面积分别增加了多少平方米.
例4
设原正方形苗圃的边长为a(m),边长增加1.5 m后,
新正方形的 边长为(a+1.5) m.
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25.
解:
当 a=30.1 时,3a+2.25=3×30.1+2.25=92.55;
当 a=29.5 时,3a+2.25=3×29.5+2.25=90.75.
答:两块苗圃的面积分别增加了 92.55 m2,90.75 m2.
在解答实际问题时,利用乘法公式会减少计算量,提高准确性.
1 若(a+b)2=(a-b)2+A,则A为( )
A.2ab B.-2ab
C.4ab D.-4ab
2 若(x+3)2=x2+ax+9,则a的值为( )
A.3 B.±3
C.6 D.±6
C
C
3 如图,图中最大的正方形的面积是( )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
C
1. 完全平方公式的特征:
左边是二项式的平方,右边是二次三项式,其中两项分别是公式左边两项的平方,中间一项是左边二项式中两项乘积的2倍.
2. 公式中的a,b可以是单项式,也可以是多项式.公式也可以逆用:a2±2ab+b2=(a±b)2.
1. 必做: 完成教材P69练习T1-2, 习题8.3T1,T7
