2020湘教版八下数学4.3一次函数的图象第2课时习题课件(30张PPT)
文档属性
| 名称 | 2020湘教版八下数学4.3一次函数的图象第2课时习题课件(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 659.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览









文档简介
课件30张PPT。4.3 一次函数的图象?
第2课时1.理解一次函数的图象是一条直线,会用两点法画一次函数的图象.(重点)
2.能根据函数的图象和函数表达式,探索并理解一次函数的性质.(重点)
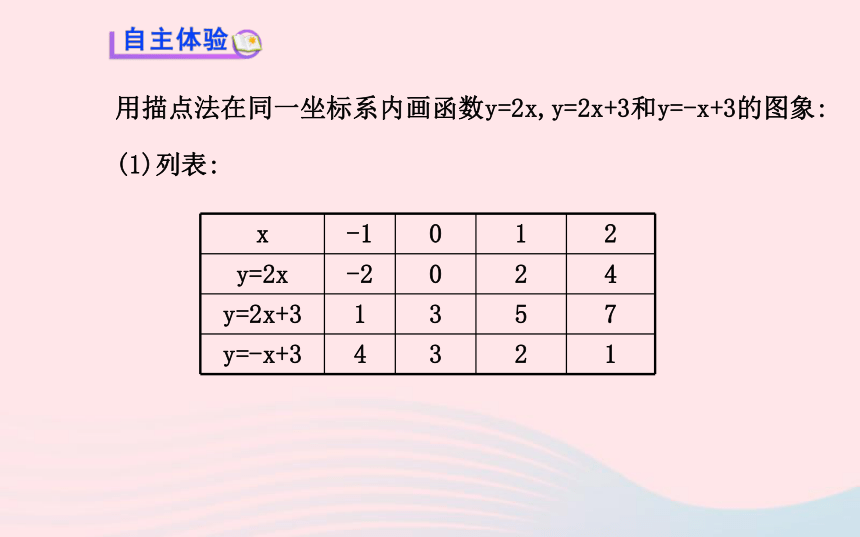
3.掌握直线y=kx+b(k≠0)与直线y=kx(k≠0)之间的关系.(难点)用描点法在同一坐标系内画函数y=2x,y=2x+3和y=-x+3的图象:
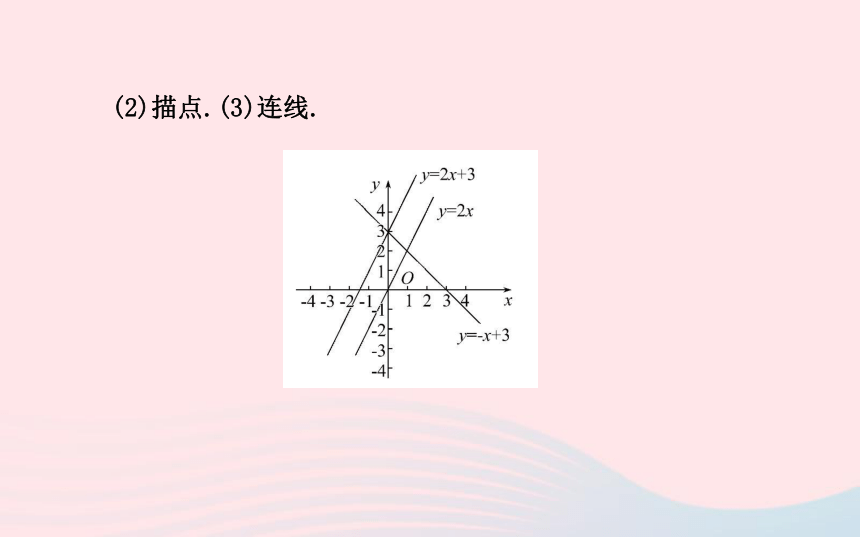
(1)列表:(2)描点.(3)连线.【思考】(1)这三个函数的共同点是它们的图象都是_____.
(2)函数y=2x和y=2x+3的位置关系如何?
提示:直线y=2x和y=2x+3互相平行.
(3)如何移动直线y=2x才能得到直线y=2x+3?
提示:把直线y=2x向上平移3个单位即可得到直线y=2x+3.直线(4)观察函数y=2x+3和y=-x+3的图象,它们的函数值y随着x值的
增大如何变化?
提示:y=2x+3的函数值y随着x值的增大而增大;y=-x+3的函数值
y随着x值的增大而减小.
(5)函数y=2x+3和y=-x+3的图象都经过点______.(0,3)【总结】
(1)一次函数y=kx+b(k≠0)的图象:
一次函数y=kx+b(k≠0)的图象是一条_____,它与正比例函数
y=kx(k≠0)的图象_____,一次函数y=kx+b(k,b为常数,k≠0)的
图象可以看作由直线y=kx平移____个单位长度而得到(当b>0时,
向___平移;当b<0时,向___平移).直线平行|b|上下(2)对于直线y=kx+b(k≠0):
当k>0,b>0时,直线经过第___________象限;
当k>0,b<0时,直线经过第___________象限;
当k<0,b>0时,直线经过第___________象限;
当k<0,b<0时,直线经过第___________象限.一、二、三一、三、四一、二、四二、三、四(3)一次函数y=kx+b(k≠0)的性质:
①当k>0时,y的值随着x值的增大而_____;
当k<0时,y的值随着x值的增大而_____.
②一次函数y=kx+b(k≠0)的图象经过点(0,b).增大减小 (打“√”或“×”)
(1)一次函数y=kx+b(k≠0)的图象经过点 ( )
(2)画一次函数的图象时只要能确定两点即可. ( )
(3)直线y=6x-3是由直线y=6x向上平移3个单位得到的.( )
(4)直线y=-2x+5与y轴的交点坐标为(0,5).( )
(5)直线y=-3x-2经过第二、三、四象限.( )×√×√√知识点 1 一次函数的图象?
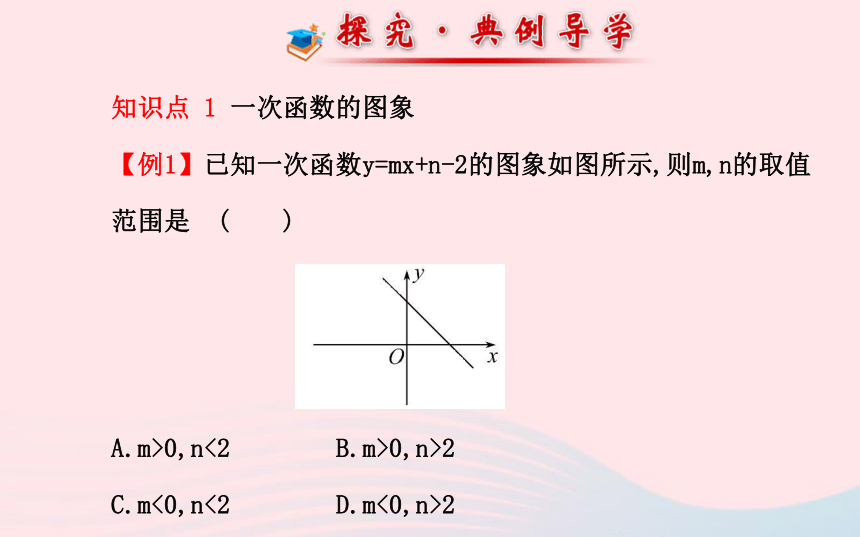
【例1】已知一次函数y=mx+n-2的图象如图所示,则m,n的取值范围是 ( )
A.m>0,n<2 B.m>0,n>2
C.m<0,n<2 D.m<0,n>2【解题探究】(1)①观察图象:直线的增减性如何?
提示:y随x的增大而减小.
②由直线的增减性得m的取值范围是:____.
(2)①图象与y轴的交点在y轴的_______.
②因此n-2__0,即____.
综上所述,选项__正确.m<0正半轴>n>2D【总结提升】k,b的正、负与直线经过的象限
一次函数y=kx+b中k,b的正、负与函数图象经过象限的关系列表如下:知识点 2 一次函数的性质?
【例2】画出函数y=x+1的图象,并根据图象回答:
(1)x为何值时,y的值为0?
(2)y为何值时,x的值为0?
(3)x为何值时,y>0?
(4)x为何值时,y随x的增大而增大?【思路点拨】过两点作出函数图象→由图象与x轴的交点情况判断y值的正负→确定函数增减性
【自主解答】过点(0,1),(-1,0)画出函数y=x+1的图象,如图所示.
(1)当x=-1时,y=0.
(2)当y=1时,x=0.
(3)当x>-1时,y>0.
(4)x取任意实数,y都随x的增大而增大.【总结提升】函数图象或增减性确定k,b的符号
1.由函数图象确定k,b的符号:
(1)确定k的符号:当函数图象过第一、三象限时,k>0;当函数图象过第二、四象限时,k<0.
(2)确定b的符号:当函数图象交y轴正半轴时,b>0;当函数图象交y轴负半轴时,b<0;当函数图象过原点时,b=0.
2.由函数的增减性确定k的符号:
(1)当y随x的增大而增大时,k>0.
(2)当y随x的增大而减小时,k<0.题组一:一次函数的图象
1.如图,一次函数y=
(m-2)x-1的图象经过第二、三、四象限,
则m的取值范围是 ( )
A.m>0 B.m<0
C.m>2 D.m<2
【解析】选D.由图象知一次函数y=(m-2)x-1经过第二、三、四象限得m-2<0,解得m<2.2.将直线y=2x向右平移1个单位后所得图象对应的函数表达式为 ( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
【解析】选B.直线y=2x向右平移1个单位后所得图象对应的函数表达式为y=2(x-1),即y=2x-2.3.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是 ( )
【解析】选A.∵正比例函数y=kx(k≠0)的函数值y随x的增大而增大,∴k>0,
∴一次函数y=x+k的图象经过第一、二、三象限.4.若一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,则k的取值范围是 .
【解析】∵一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,∴k>0.
答案:k>05.一次函数y=2x-1的图象经过点(a,3),则a= .
【解析】∵一次函数y=2x-1的图象经过点(a,3),
∴3=2a-1,解得a=2.
答案:2题组二:一次函数的性质
1.下列函数中,y随x的增大而减小的函数是 ( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
【解析】选C.由y随x的增大而减小,可知k<0.2.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是 ( )
A.m<0 B.m>0 C.m<2 D.m>2
【解析】选D.∵一次函数y=(2-m)x-2的函数值y随x的增大而减小,∴2-m<0,∴m>2.3.在一次函数y=(2-k)x+1中,y随x的增大而增大,则k的取值范围为 .
【解析】∵一次函数y=(2-k)x+1中,y随x的增大而增大,∴2-k>0,∴k<2.
答案:k<24.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a b.(填“>”“<”或“=”)
【解析】∵直线y=-3x+2中,k=-3<0,
∴函数值y随自变量x的增大而减小.
∵-5<4,∴a>b.
答案:>5.某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如下表所示:(1)若商场预计进货费用为3500元,则这两种台灯各购进多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
【解析】设商场应购进A型台灯x盏,则购进B型台灯(100-x)盏,
(1)根据题意得:30x+50(100-x)=3500,
解得x=75,∴100-x=25.
答:应购进A型台灯75盏,B型台灯25盏.(2)设商场销售完这批台灯可获利y元,则
y=(45-30)x+(70-50)(100-x)
=15x+20(100-x)=-5x+2000,
由题意得100-x≤3x,解得x≥25,
∵k=-5<0,∴y随x的增大而减小,
∴当x=25时,y取最大值:-5×25+2000=1875(元).
答:商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯获利最多,此时利润为1875元.【想一想错在哪?】直线y= x+2与x轴、y轴分别交于A,B两
点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标.
(2)当S=12时,求点D的坐标.提示:忽略了点D在点A左侧的情况而出错.
第2课时1.理解一次函数的图象是一条直线,会用两点法画一次函数的图象.(重点)
2.能根据函数的图象和函数表达式,探索并理解一次函数的性质.(重点)
3.掌握直线y=kx+b(k≠0)与直线y=kx(k≠0)之间的关系.(难点)用描点法在同一坐标系内画函数y=2x,y=2x+3和y=-x+3的图象:
(1)列表:(2)描点.(3)连线.【思考】(1)这三个函数的共同点是它们的图象都是_____.
(2)函数y=2x和y=2x+3的位置关系如何?
提示:直线y=2x和y=2x+3互相平行.
(3)如何移动直线y=2x才能得到直线y=2x+3?
提示:把直线y=2x向上平移3个单位即可得到直线y=2x+3.直线(4)观察函数y=2x+3和y=-x+3的图象,它们的函数值y随着x值的
增大如何变化?
提示:y=2x+3的函数值y随着x值的增大而增大;y=-x+3的函数值
y随着x值的增大而减小.
(5)函数y=2x+3和y=-x+3的图象都经过点______.(0,3)【总结】
(1)一次函数y=kx+b(k≠0)的图象:
一次函数y=kx+b(k≠0)的图象是一条_____,它与正比例函数
y=kx(k≠0)的图象_____,一次函数y=kx+b(k,b为常数,k≠0)的
图象可以看作由直线y=kx平移____个单位长度而得到(当b>0时,
向___平移;当b<0时,向___平移).直线平行|b|上下(2)对于直线y=kx+b(k≠0):
当k>0,b>0时,直线经过第___________象限;
当k>0,b<0时,直线经过第___________象限;
当k<0,b>0时,直线经过第___________象限;
当k<0,b<0时,直线经过第___________象限.一、二、三一、三、四一、二、四二、三、四(3)一次函数y=kx+b(k≠0)的性质:
①当k>0时,y的值随着x值的增大而_____;
当k<0时,y的值随着x值的增大而_____.
②一次函数y=kx+b(k≠0)的图象经过点(0,b).增大减小 (打“√”或“×”)
(1)一次函数y=kx+b(k≠0)的图象经过点 ( )
(2)画一次函数的图象时只要能确定两点即可. ( )
(3)直线y=6x-3是由直线y=6x向上平移3个单位得到的.( )
(4)直线y=-2x+5与y轴的交点坐标为(0,5).( )
(5)直线y=-3x-2经过第二、三、四象限.( )×√×√√知识点 1 一次函数的图象?
【例1】已知一次函数y=mx+n-2的图象如图所示,则m,n的取值范围是 ( )
A.m>0,n<2 B.m>0,n>2
C.m<0,n<2 D.m<0,n>2【解题探究】(1)①观察图象:直线的增减性如何?
提示:y随x的增大而减小.
②由直线的增减性得m的取值范围是:____.
(2)①图象与y轴的交点在y轴的_______.
②因此n-2__0,即____.
综上所述,选项__正确.m<0正半轴>n>2D【总结提升】k,b的正、负与直线经过的象限
一次函数y=kx+b中k,b的正、负与函数图象经过象限的关系列表如下:知识点 2 一次函数的性质?
【例2】画出函数y=x+1的图象,并根据图象回答:
(1)x为何值时,y的值为0?
(2)y为何值时,x的值为0?
(3)x为何值时,y>0?
(4)x为何值时,y随x的增大而增大?【思路点拨】过两点作出函数图象→由图象与x轴的交点情况判断y值的正负→确定函数增减性
【自主解答】过点(0,1),(-1,0)画出函数y=x+1的图象,如图所示.
(1)当x=-1时,y=0.
(2)当y=1时,x=0.
(3)当x>-1时,y>0.
(4)x取任意实数,y都随x的增大而增大.【总结提升】函数图象或增减性确定k,b的符号
1.由函数图象确定k,b的符号:
(1)确定k的符号:当函数图象过第一、三象限时,k>0;当函数图象过第二、四象限时,k<0.
(2)确定b的符号:当函数图象交y轴正半轴时,b>0;当函数图象交y轴负半轴时,b<0;当函数图象过原点时,b=0.
2.由函数的增减性确定k的符号:
(1)当y随x的增大而增大时,k>0.
(2)当y随x的增大而减小时,k<0.题组一:一次函数的图象
1.如图,一次函数y=
(m-2)x-1的图象经过第二、三、四象限,
则m的取值范围是 ( )
A.m>0 B.m<0
C.m>2 D.m<2
【解析】选D.由图象知一次函数y=(m-2)x-1经过第二、三、四象限得m-2<0,解得m<2.2.将直线y=2x向右平移1个单位后所得图象对应的函数表达式为 ( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
【解析】选B.直线y=2x向右平移1个单位后所得图象对应的函数表达式为y=2(x-1),即y=2x-2.3.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是 ( )
【解析】选A.∵正比例函数y=kx(k≠0)的函数值y随x的增大而增大,∴k>0,
∴一次函数y=x+k的图象经过第一、二、三象限.4.若一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,则k的取值范围是 .
【解析】∵一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,∴k>0.
答案:k>05.一次函数y=2x-1的图象经过点(a,3),则a= .
【解析】∵一次函数y=2x-1的图象经过点(a,3),
∴3=2a-1,解得a=2.
答案:2题组二:一次函数的性质
1.下列函数中,y随x的增大而减小的函数是 ( )
A.y=2x+8 B.y=-2+4x
C.y=-2x+8 D.y=4x
【解析】选C.由y随x的增大而减小,可知k<0.2.若一次函数y=(2-m)x-2的函数值y随x的增大而减小,则m的取值范围是 ( )
A.m<0 B.m>0 C.m<2 D.m>2
【解析】选D.∵一次函数y=(2-m)x-2的函数值y随x的增大而减小,∴2-m<0,∴m>2.3.在一次函数y=(2-k)x+1中,y随x的增大而增大,则k的取值范围为 .
【解析】∵一次函数y=(2-k)x+1中,y随x的增大而增大,∴2-k>0,∴k<2.
答案:k<24.已知点A(-5,a),B(4,b)在直线y=-3x+2上,则a b.(填“>”“<”或“=”)
【解析】∵直线y=-3x+2中,k=-3<0,
∴函数值y随自变量x的增大而减小.
∵-5<4,∴a>b.
答案:>5.某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如下表所示:(1)若商场预计进货费用为3500元,则这两种台灯各购进多少盏?
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
【解析】设商场应购进A型台灯x盏,则购进B型台灯(100-x)盏,
(1)根据题意得:30x+50(100-x)=3500,
解得x=75,∴100-x=25.
答:应购进A型台灯75盏,B型台灯25盏.(2)设商场销售完这批台灯可获利y元,则
y=(45-30)x+(70-50)(100-x)
=15x+20(100-x)=-5x+2000,
由题意得100-x≤3x,解得x≥25,
∵k=-5<0,∴y随x的增大而减小,
∴当x=25时,y取最大值:-5×25+2000=1875(元).
答:商场购进A型台灯25盏,B型台灯75盏,销售完这批台灯获利最多,此时利润为1875元.【想一想错在哪?】直线y= x+2与x轴、y轴分别交于A,B两
点,D是x轴上一点,坐标为(x,0),△ABD的面积为S.
(1)求点A和点B的坐标.
(2)当S=12时,求点D的坐标.提示:忽略了点D在点A左侧的情况而出错.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
