沪科版数学八年级下册 18.1.1勾股定理课件(16张)
文档属性
| 名称 | 沪科版数学八年级下册 18.1.1勾股定理课件(16张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
新课导入
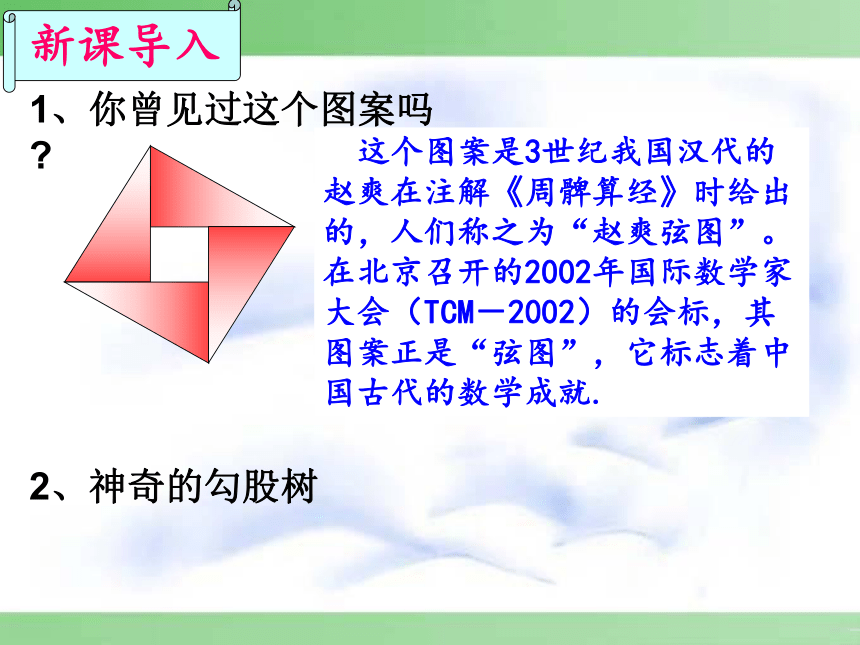
1、你曾见过这个图案吗?
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”。在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
2、神奇的勾股树
18.1.1勾股定理
1、理解并掌握勾股定理,探索勾股定理
的证明过程;
2、会运用勾股定理解决简单的实际问题.
学习目标
独立自学
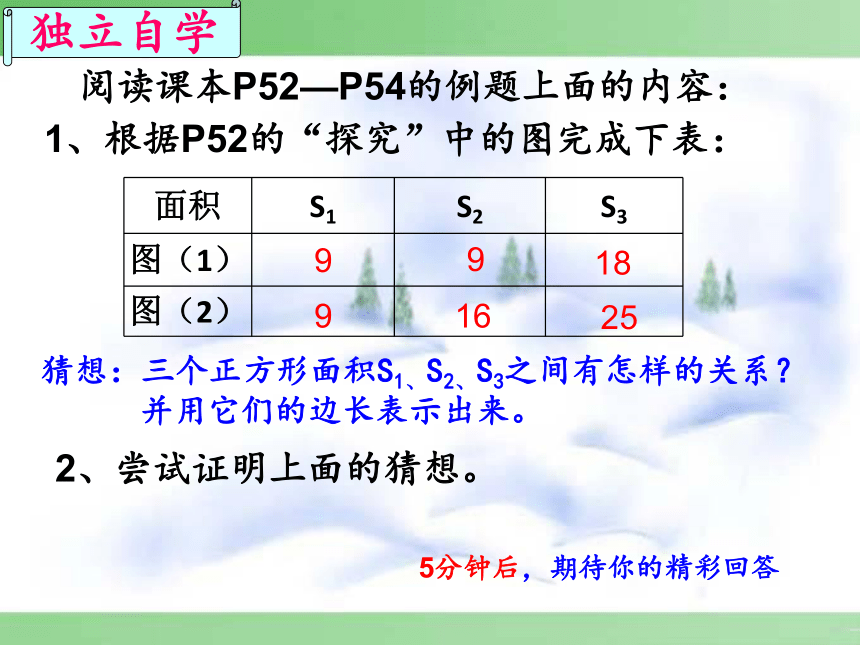
阅读课本P52—P54的例题上面的内容:
1、根据P52的“探究”中的图完成下表:
猜想:三个正方形面积S1、S2、S3之间有怎样的关系?
并用它们的边长表示出来。
2、尝试证明上面的猜想。
5分钟后,期待你的精彩回答
9
9
18
9
16
25
面积 S1 S2 S3
图(1)
图(2)
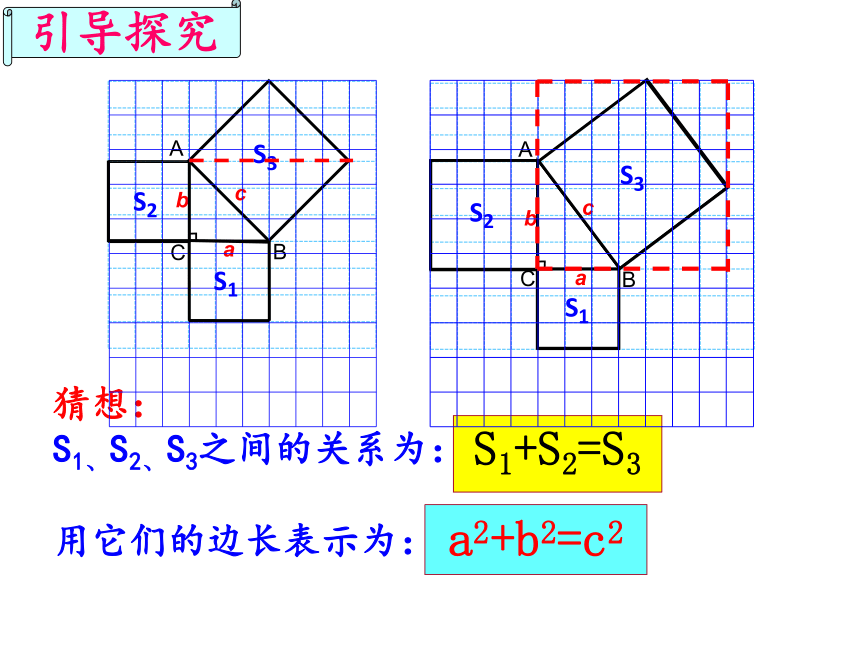
S1、S2、S3之间的关系为:
用它们的边长表示为:
引导探究
S1+S2=S3
a2+b2=c2
猜想:
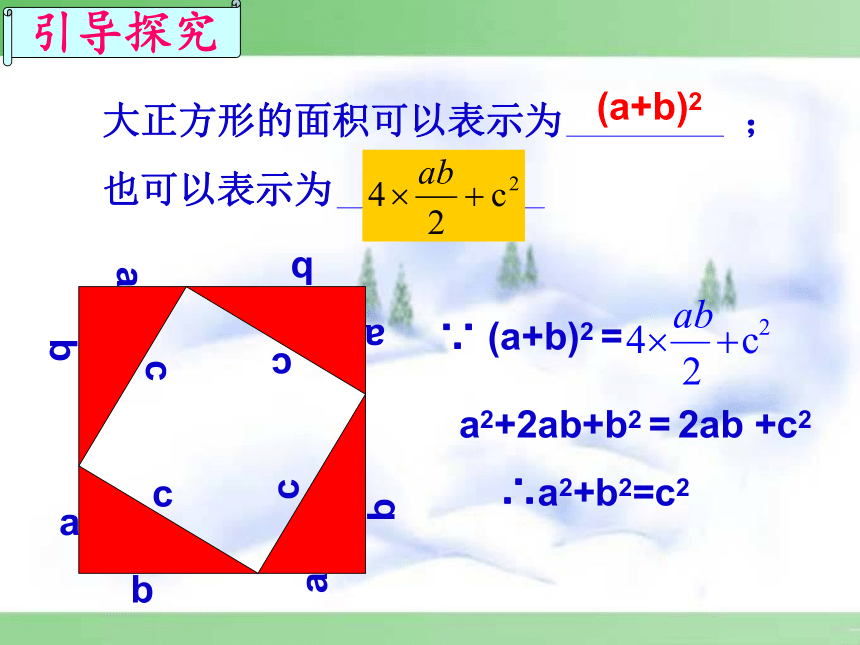
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
引导探究
勾股定理
(毕达哥拉斯定理)
直角三角形两直角边的平方和等于斜边的平方.
┏
a2+b2=c2
a
c
b
勾
股
弦
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
引导探究
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
你能只用这两个直角三角形说明a2+b2=c2吗?
引导探究
1、在Rt△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
a
c
b
学以致用
变式
有一个直角三角形的两条边长为3和4,则第三边长为 .
学以致用
2、已知:如图,在Rt△ABC中,两直角边AC=5,BC=12,求斜边上的高CD的长。
方法指导:勾股定理与面积法
学以致用
3、现有一楼房发生火灾,消防员决定用消防车上的云梯救人,如图。已知云梯最多只能伸长到10m,消防车高3m,救人时云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原来处再向着火的楼房靠近多少米?(精确到0.1m)
无字证明
a
b
c
无字证明
青出
青朱出入图
目标再现
这堂课你收获
了什么?
1、理解并掌握勾股定理,探索勾股定理
的证明过程。
2、会运用勾股定理解决简单的实际问题。
新课导入
1、你曾见过这个图案吗?
这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称之为“赵爽弦图”。在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就.
2、神奇的勾股树
18.1.1勾股定理
1、理解并掌握勾股定理,探索勾股定理
的证明过程;
2、会运用勾股定理解决简单的实际问题.
学习目标
独立自学
阅读课本P52—P54的例题上面的内容:
1、根据P52的“探究”中的图完成下表:
猜想:三个正方形面积S1、S2、S3之间有怎样的关系?
并用它们的边长表示出来。
2、尝试证明上面的猜想。
5分钟后,期待你的精彩回答
9
9
18
9
16
25
面积 S1 S2 S3
图(1)
图(2)
S1、S2、S3之间的关系为:
用它们的边长表示为:
引导探究
S1+S2=S3
a2+b2=c2
猜想:
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
引导探究
勾股定理
(毕达哥拉斯定理)
直角三角形两直角边的平方和等于斜边的平方.
┏
a2+b2=c2
a
c
b
勾
股
弦
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
引导探究
1881年,伽菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为“总统证法”.
你能只用这两个直角三角形说明a2+b2=c2吗?
引导探究
1、在Rt△ABC中∠C=90°,
⑴若a=4,b=3,则c=____
⑵若c=13,b=5,则a=____
⑶ 若 c=17,a=8,则b=____
5
12
15
a
c
b
学以致用
变式
有一个直角三角形的两条边长为3和4,则第三边长为 .
学以致用
2、已知:如图,在Rt△ABC中,两直角边AC=5,BC=12,求斜边上的高CD的长。
方法指导:勾股定理与面积法
学以致用
3、现有一楼房发生火灾,消防员决定用消防车上的云梯救人,如图。已知云梯最多只能伸长到10m,消防车高3m,救人时云梯伸至最长,在完成从9m高处救人后,还要从12m高处救人,这时消防车要从原来处再向着火的楼房靠近多少米?(精确到0.1m)
无字证明
a
b
c
无字证明
青出
青朱出入图
目标再现
这堂课你收获
了什么?
1、理解并掌握勾股定理,探索勾股定理
的证明过程。
2、会运用勾股定理解决简单的实际问题。
