沪科版七下数学10.2 平行线的判定之用同位角判定两直线平行教学课件(30张)
文档属性
| 名称 | 沪科版七下数学10.2 平行线的判定之用同位角判定两直线平行教学课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 968.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 15:37:06 | ||
图片预览










文档简介
(共30张PPT)
10.2 平行线的判定
用“同位角”、“第三直线”
判定平行线
第10章 相交线、平行线与平移
1
课堂讲解
同位角相等,两直线平行
在同一平面内,垂直于同一条直线的两条直线平行
2
课时流程
作业提升
逐点
导讲练
课堂小结
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
1
知识点
同位角相等,两直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
这是判定两条直线平行的第1种方法.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
表达方式:如图:因为∠1=∠2(已知),
所以a∥b(同位角相等,两直线平行).
要点精析:
(1)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行);它构建起角的大小关系与直线的位置关系的桥梁.
(2)“同位角相等”是判定“两直线平行”的一个定量标准.
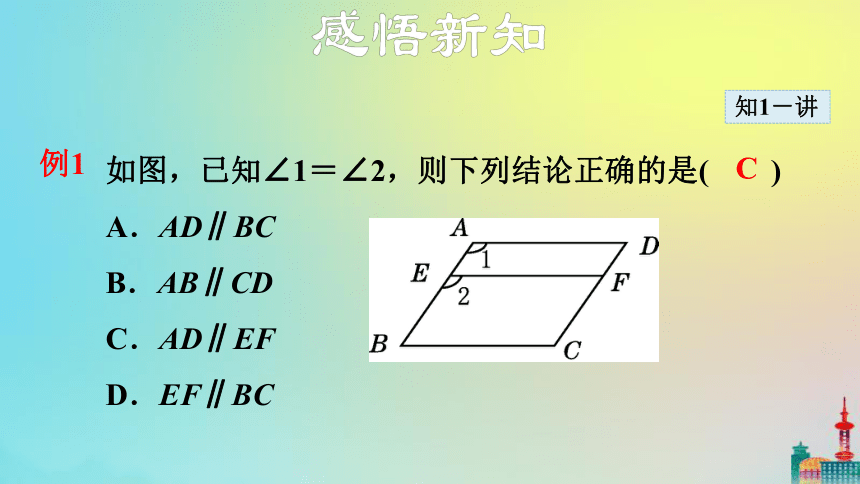
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
例1
C
导引:
要判定哪两条直线平行,就是要确定∠1,∠2是哪两条直线被第三条直线所截得到的同位角,即找出∠1,∠2除公共边外的另两边.
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;再根据“同位角相等,两直线平行”推导出这两条直线平行.
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
例2
导引:
垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
解:
这两条直线平行.理由如下:
如图. ∵b⊥a,∴∠1=90°.
同理∠2=90°.
∴∠1=∠2.
∵∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
1 (中考·百色)如图,直线a,b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
B
2 如图所示,用直尺和三角尺作直线,从图中可知,直线AB与直线CD的位置关系为________,理由是________________________.
AB // CD
同位角相等,两直线平行
3 如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
D
4 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
C
2
知识点
在同一平面内,垂直于同一条直线的两条直线平行
如图,你能说出木工用图中的角尺画平行线的道理吗?
如图所示,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作CD的平行线,则只需过点E作岸AB的平行线即可.其理由是什么?
例3
导引:
利用平行线的性质,把实际问题转化为数学问题回答.
解:
理由是
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如图,已知直线a,b,c,d,e,且∠1=∠2,
∠3=∠4,则a与c平行吗?为什么?
例4
解:a与c平行.
理由:因为∠1=∠2(______________),
所以a∥b(________________________).
因为∠3=∠4(__________________),
所以b∥c(_________________________).
所以a∥c(________________________________).
已知
同位角相等,两直线平行
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
如图,已知∠1=90°,∠2=90°,
试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
例5
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
解:
1 在每一步推理后面的括号内填上理由.
(1)如图①,
因为AB∥CD,EF∥CD,
所以AB∥EF(_________
__________________________________).
平行于同一条直线的两条直线平行
(2)如图②,
因为AB∥CD,
过点F画EF∥AB(_____________
_________________________________),
所以EF∥CD(________________________________).
有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
过直线外一点,
2 在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
D
3 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
B
判断两直线平行的方法:
(1)平面内不相交的两直线(平行线的定义)?两直线平行.
(2)同平行于第三条直线的两条直线 (平行线基本事实的推论)?两直线平行.
(3)同位角相等(判定方法1)?两直线平行.
1. 必做: 完成教材P126练习T1-T3,习题10.2T3
10.2 平行线的判定
用“同位角”、“第三直线”
判定平行线
第10章 相交线、平行线与平移
1
课堂讲解
同位角相等,两直线平行
在同一平面内,垂直于同一条直线的两条直线平行
2
课时流程
作业提升
逐点
导讲练
课堂小结
装修工人正在向墙上钉木条,如果木条b与墙壁边缘垂直,那么木条a与墙壁边缘所夹角为多少度时,才能使木条a与木条b平行?
1
知识点
同位角相等,两直线平行
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
这是判定两条直线平行的第1种方法.
方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简称:同位角相等,两直线平行.
表达方式:如图:因为∠1=∠2(已知),
所以a∥b(同位角相等,两直线平行).
要点精析:
(1)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行);它构建起角的大小关系与直线的位置关系的桥梁.
(2)“同位角相等”是判定“两直线平行”的一个定量标准.
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
例1
C
导引:
要判定哪两条直线平行,就是要确定∠1,∠2是哪两条直线被第三条直线所截得到的同位角,即找出∠1,∠2除公共边外的另两边.
利用同位角相等来判定两直线平行的方法:
首先要找出这对同位角是哪两条直线被第三条直线所截形成的;再根据“同位角相等,两直线平行”推导出这两条直线平行.
在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
例2
导引:
垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
解:
这两条直线平行.理由如下:
如图. ∵b⊥a,∴∠1=90°.
同理∠2=90°.
∴∠1=∠2.
∵∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
判断两条直线是否平行,可以找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行.
1 (中考·百色)如图,直线a,b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6
B.∠2=∠6
C.∠1=∠3
D.∠5=∠7
B
2 如图所示,用直尺和三角尺作直线,从图中可知,直线AB与直线CD的位置关系为________,理由是________________________.
AB // CD
同位角相等,两直线平行
3 如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
D
4 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
C
2
知识点
在同一平面内,垂直于同一条直线的两条直线平行
如图,你能说出木工用图中的角尺画平行线的道理吗?
如图所示,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作CD的平行线,则只需过点E作岸AB的平行线即可.其理由是什么?
例3
导引:
利用平行线的性质,把实际问题转化为数学问题回答.
解:
理由是
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
如图,已知直线a,b,c,d,e,且∠1=∠2,
∠3=∠4,则a与c平行吗?为什么?
例4
解:a与c平行.
理由:因为∠1=∠2(______________),
所以a∥b(________________________).
因为∠3=∠4(__________________),
所以b∥c(_________________________).
所以a∥c(________________________________).
已知
同位角相等,两直线平行
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
如图,已知∠1=90°,∠2=90°,
试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
例5
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
解:
1 在每一步推理后面的括号内填上理由.
(1)如图①,
因为AB∥CD,EF∥CD,
所以AB∥EF(_________
__________________________________).
平行于同一条直线的两条直线平行
(2)如图②,
因为AB∥CD,
过点F画EF∥AB(_____________
_________________________________),
所以EF∥CD(________________________________).
有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
过直线外一点,
2 在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )
A.互相平行 B.互相垂直
C.共线 D.互相平行或共线
D
3 三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )
A.a⊥b B.a∥b
C.a⊥b或a∥b D.无法确定
B
判断两直线平行的方法:
(1)平面内不相交的两直线(平行线的定义)?两直线平行.
(2)同平行于第三条直线的两条直线 (平行线基本事实的推论)?两直线平行.
(3)同位角相等(判定方法1)?两直线平行.
1. 必做: 完成教材P126练习T1-T3,习题10.2T3
