沪科版七下数学10.3 平行线的性质教学课件(45张)
文档属性
| 名称 | 沪科版七下数学10.3 平行线的性质教学课件(45张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 15:49:34 | ||
图片预览










文档简介
(共45张PPT)
10.3 平行线的性质
平行线的性质
第10章 相交线、平行线与平移
1
课堂讲解
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
2
课时流程
作业提升
逐点
导讲练
课堂小结
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?这就是我们下面要学习的平行线的性质.
类似于研究平行线的判定,我们先来研究两条直线平行时.它们被第三条直线截得的同位角的关系.
1
知识点
两直线平行,同位角相等
观察
如图,练习本上的横线都是相
互平行的,从中任选两条分别记为
AB,CD;画一条直线EF分别与
AB, CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),
量一量 它们的度数,它们的大
小有什么关系?
由此你能得到什么结论?
平行线有如下性质:
性质1 两条平行线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
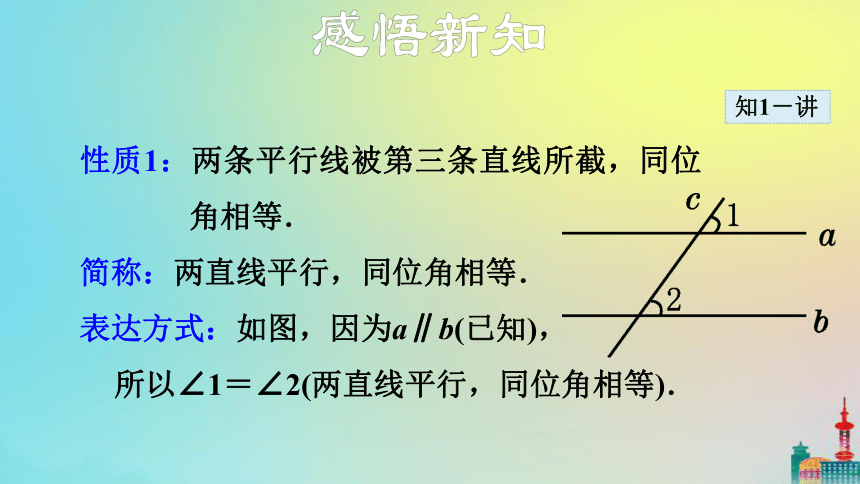
性质1:两条平行线被第三条直线所截,同位角相等.
简称:两直线平行,同位角相等.
表达方式:如图,因为a∥b(已知),
所以∠1=∠2(两直线平行,同位角相等).
要点精析:
(1)两直线平行是前提,只有在这个前提下才有同位角相等.
(2)平行线的判定与平行线的性质的区别:
①平行线的判定是根据两角的数量关系得到两条直线的位置关系,而平行线的性质是根据两条直线的位置关系得到两角的数量关系;
②平行线的判定的条件是平行线的性质的结论,而平行线的判定的结论是平行线的性质的条件.
2. 易错警示:误认为非平行线的同位角也相等.
如图,直线a∥b,直线c与a,b相交,∠1=70°,则∠2的大小是( )
A.20° B.50°
C.70° D.110°
例1
C
导引:
观察图形可以把求∠2转化为求∠2的对顶角来解,因为∠2的对顶角与∠1是同位角,而直线a∥b,所以∠2=∠1=70°.
有关两直线平行,同位角相等的性质,分清两个角的位置关系是解答此类题目的关键.
如图,若AB∥CD,且∠1=∠2,试判断AM与CN的位置关系,并说明理由.
例2
解:
AM∥CN.
理由:因为AB∥CD(已知),
所以∠BAE=∠ACD(两直线平行,同位角相等).
又因为∠1=∠2(已知),
所以∠MAE=∠NCA(等式的性质).
所以AM∥CN(同位角相等,两直线平行).
当题目已知条件中出现两直线平行时,要考虑是否出现了相等的角.平行线和角的大小关系是紧密联系在一起的,由平行线可以得到相等的角,反过来又可以由相等的角得到新的一组平行线,这种由角的大小关系与直线的位置关系的相互转化在解题中会经常涉及.
1 (中考· 荆州)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
A.70° B.80°
C.110° D.120°
C
2 (中考· 咸宁)如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
A.50° B.40°
C.30° D.25°
B
2
知识点
两直线平行,内错角相等
思考
在下图中,当AB∥CD时,你还会发现内错角∠3和∠5的大小有什么关系?能说明理由吗?
如图,直线a∥b,c是截线.
根据“两直线平行,同位角相等”,
可得∠2=∠3.而∠3和∠1互为对
顶角,所以∠3=∠1.所以∠l=∠2.
这样,我们就得到了平行线的另一
个性质:
性质2 两条平行线被第三条直线所截,内错角相等. 简单地说,两直线平行,内错角相等.
1. 性质2:两条平行线被第三条直线所截,内错角相等.
简称:两直线平行,内错角相等.
表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
要点精析:两直线平行是前提,只有在这个前提下才有内错角相等.
2. 易错警示:找准平行线的内错角.
如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
例3
导引:
要说明AE平分∠CAD,即说明∠DAE=∠CAE.
由于AE∥BC,根据两直线平行,同位角相等和内错角相等可知∠DAE=∠B,∠EAC=∠C,这就将说明∠DAE=∠CAE转化为说明∠B=∠C了.
解:
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),∠EAC=∠C(两直线平行,内错角相等),因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
本题同时运用了“两直线平行,同位角相等”和“两直线平行,内错角相等”提供了一种说明两个角相等的新思路.
1 (中考· 邵阳)将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.30°
B.45°
C.60°
D.65°
C
2 (中考· 荆门)如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
A.35°
B.45°
C.55°
D.65
C
3
知识点
两直线平行,同旁内角互补
1. 性质3:两条平行线被第三条直线所截,同旁内角互补.
简称:两直线平行,同旁内角互补.
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
2. 易错警示:平行线的同旁内角是互补不是相等.
如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
例4
导引:
由DE∥BC,可得∠1=∠4,
∠1+∠2=180°;
由DF∥AB,可得∠3=∠2,
从而得∠2,∠3,∠4的度数.
解:
因为DE∥BC(已知),
所以∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB(已知),
所以∠3=∠2(两直线平行,同位角相等).
所以∠3=115°(等量代换).
(1)求角的度数的基本思路:根据平行线的判定由角的数量关系得到直线的位置关系,根据平行线的性质由直线的位置关系得到角的数量关系,通过上述相互转化,从而找到所求角与已知角之间的关系.
(2)两直线平行时,应联想到平行线的三个性质,由两条直线平行的位置关系得到两个相关角的数量关系,由角的关系求相应角的度数.
如图,已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,
试说明BC⊥AB.
例5
要说明BC⊥AB,即说明∠B=90°.因为DA⊥AB,所以若能说明AD∥CB,则BC⊥AB. 由DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,可说明∠ADC+∠BCD=180°,从而说明AD∥BC.
导引:
因为DE平分∠ADC,CE平分∠BCD,
所以∠1=∠3,∠2=∠4(角平分线的定义).
因为∠1+∠2=90°,
所以∠1+∠2+∠3+∠4=180°,
即∠ADC+∠BCD=180°.
所以AD∥BC(同旁内角互补,两直线平行),
解:
所以∠A+∠B=180°(两直线平行,同旁内角互补).
因为DA⊥AB,所以∠A=90°(垂直的定义).
所以∠B=90°,即BC⊥AB(垂直的定义).
平行线和角的大小关系、直线的位置关系等是紧密联系在一起的,通过一对同位角相等或内错角相等或同旁内角互补可以判断两直线平行,反过来可以根据两直线平行判断同位角相等、内错角相等或同旁内角互补,再利用这些相等、互补关系说明
其他结论;因此两直线平行好似一座桥梁,将原本没有关系的数学问题建立起联系.
1 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=________.
111°
2 (中考· 北京)如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
A.26°
B.36°
C.46°
D.56°
B
1. 平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2. 平行线的性质与平行线的判定的区别.
判定:角的关系→平行的关系
性质:平行的关系→角的关系
1. 必做: 完成教材P130练习T1-T3
10.3 平行线的性质
平行线的性质
第10章 相交线、平行线与平移
1
课堂讲解
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
2
课时流程
作业提升
逐点
导讲练
课堂小结
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?这就是我们下面要学习的平行线的性质.
类似于研究平行线的判定,我们先来研究两条直线平行时.它们被第三条直线截得的同位角的关系.
1
知识点
两直线平行,同位角相等
观察
如图,练习本上的横线都是相
互平行的,从中任选两条分别记为
AB,CD;画一条直线EF分别与
AB, CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),
量一量 它们的度数,它们的大
小有什么关系?
由此你能得到什么结论?
平行线有如下性质:
性质1 两条平行线被第三条直线所截,同位角相等.
简单地说,两直线平行,同位角相等.
性质1:两条平行线被第三条直线所截,同位角相等.
简称:两直线平行,同位角相等.
表达方式:如图,因为a∥b(已知),
所以∠1=∠2(两直线平行,同位角相等).
要点精析:
(1)两直线平行是前提,只有在这个前提下才有同位角相等.
(2)平行线的判定与平行线的性质的区别:
①平行线的判定是根据两角的数量关系得到两条直线的位置关系,而平行线的性质是根据两条直线的位置关系得到两角的数量关系;
②平行线的判定的条件是平行线的性质的结论,而平行线的判定的结论是平行线的性质的条件.
2. 易错警示:误认为非平行线的同位角也相等.
如图,直线a∥b,直线c与a,b相交,∠1=70°,则∠2的大小是( )
A.20° B.50°
C.70° D.110°
例1
C
导引:
观察图形可以把求∠2转化为求∠2的对顶角来解,因为∠2的对顶角与∠1是同位角,而直线a∥b,所以∠2=∠1=70°.
有关两直线平行,同位角相等的性质,分清两个角的位置关系是解答此类题目的关键.
如图,若AB∥CD,且∠1=∠2,试判断AM与CN的位置关系,并说明理由.
例2
解:
AM∥CN.
理由:因为AB∥CD(已知),
所以∠BAE=∠ACD(两直线平行,同位角相等).
又因为∠1=∠2(已知),
所以∠MAE=∠NCA(等式的性质).
所以AM∥CN(同位角相等,两直线平行).
当题目已知条件中出现两直线平行时,要考虑是否出现了相等的角.平行线和角的大小关系是紧密联系在一起的,由平行线可以得到相等的角,反过来又可以由相等的角得到新的一组平行线,这种由角的大小关系与直线的位置关系的相互转化在解题中会经常涉及.
1 (中考· 荆州)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=70°,则∠2=( )
A.70° B.80°
C.110° D.120°
C
2 (中考· 咸宁)如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
A.50° B.40°
C.30° D.25°
B
2
知识点
两直线平行,内错角相等
思考
在下图中,当AB∥CD时,你还会发现内错角∠3和∠5的大小有什么关系?能说明理由吗?
如图,直线a∥b,c是截线.
根据“两直线平行,同位角相等”,
可得∠2=∠3.而∠3和∠1互为对
顶角,所以∠3=∠1.所以∠l=∠2.
这样,我们就得到了平行线的另一
个性质:
性质2 两条平行线被第三条直线所截,内错角相等. 简单地说,两直线平行,内错角相等.
1. 性质2:两条平行线被第三条直线所截,内错角相等.
简称:两直线平行,内错角相等.
表达方式:如图,
因为a∥b(已知),
所以∠1=∠2(两直线平行,内错角相等).
要点精析:两直线平行是前提,只有在这个前提下才有内错角相等.
2. 易错警示:找准平行线的内错角.
如图,已知∠B=∠C,AE∥BC,试说明AE平分∠CAD.
例3
导引:
要说明AE平分∠CAD,即说明∠DAE=∠CAE.
由于AE∥BC,根据两直线平行,同位角相等和内错角相等可知∠DAE=∠B,∠EAC=∠C,这就将说明∠DAE=∠CAE转化为说明∠B=∠C了.
解:
因为AE∥BC(已知),
所以∠DAE=∠B(两直线平行,同位角相等),∠EAC=∠C(两直线平行,内错角相等),因为∠B=∠C(已知),
所以∠DAE=∠EAC(等量代换).
所以AE平分∠CAD(角平分线的定义).
本题同时运用了“两直线平行,同位角相等”和“两直线平行,内错角相等”提供了一种说明两个角相等的新思路.
1 (中考· 邵阳)将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )
A.30°
B.45°
C.60°
D.65°
C
2 (中考· 荆门)如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
A.35°
B.45°
C.55°
D.65
C
3
知识点
两直线平行,同旁内角互补
1. 性质3:两条平行线被第三条直线所截,同旁内角互补.
简称:两直线平行,同旁内角互补.
表达方式:如图,
因为a∥b(已知),
所以∠1+∠2=180°(两直线平行,同旁内角互补).
2. 易错警示:平行线的同旁内角是互补不是相等.
如图,如果AB∥DF,DE∥BC,且∠1=65°,那么你能说出∠2,∠3,∠4的度数吗?为什么?
例4
导引:
由DE∥BC,可得∠1=∠4,
∠1+∠2=180°;
由DF∥AB,可得∠3=∠2,
从而得∠2,∠3,∠4的度数.
解:
因为DE∥BC(已知),
所以∠4=∠1=65°(两直线平行,内错角相等),
∠2+∠1=180°(两直线平行,同旁内角互补).
所以∠2=180°-∠1=180°-65°=115°.
又因为DF∥AB(已知),
所以∠3=∠2(两直线平行,同位角相等).
所以∠3=115°(等量代换).
(1)求角的度数的基本思路:根据平行线的判定由角的数量关系得到直线的位置关系,根据平行线的性质由直线的位置关系得到角的数量关系,通过上述相互转化,从而找到所求角与已知角之间的关系.
(2)两直线平行时,应联想到平行线的三个性质,由两条直线平行的位置关系得到两个相关角的数量关系,由角的关系求相应角的度数.
如图,已知DA⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,
试说明BC⊥AB.
例5
要说明BC⊥AB,即说明∠B=90°.因为DA⊥AB,所以若能说明AD∥CB,则BC⊥AB. 由DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,可说明∠ADC+∠BCD=180°,从而说明AD∥BC.
导引:
因为DE平分∠ADC,CE平分∠BCD,
所以∠1=∠3,∠2=∠4(角平分线的定义).
因为∠1+∠2=90°,
所以∠1+∠2+∠3+∠4=180°,
即∠ADC+∠BCD=180°.
所以AD∥BC(同旁内角互补,两直线平行),
解:
所以∠A+∠B=180°(两直线平行,同旁内角互补).
因为DA⊥AB,所以∠A=90°(垂直的定义).
所以∠B=90°,即BC⊥AB(垂直的定义).
平行线和角的大小关系、直线的位置关系等是紧密联系在一起的,通过一对同位角相等或内错角相等或同旁内角互补可以判断两直线平行,反过来可以根据两直线平行判断同位角相等、内错角相等或同旁内角互补,再利用这些相等、互补关系说明
其他结论;因此两直线平行好似一座桥梁,将原本没有关系的数学问题建立起联系.
1 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=21°,那么∠2=________.
111°
2 (中考· 北京)如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=124°,∠2=88°,则∠3的度数为( )
A.26°
B.36°
C.46°
D.56°
B
1. 平行线的三个性质:
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2. 平行线的性质与平行线的判定的区别.
判定:角的关系→平行的关系
性质:平行的关系→角的关系
1. 必做: 完成教材P130练习T1-T3
