2020湘教版八下数学第4章一次函数4.3一次函数的图象第1课时习题课件(27张PPT)
文档属性
| 名称 | 2020湘教版八下数学第4章一次函数4.3一次函数的图象第1课时习题课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 583.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-14 00:00:00 | ||
图片预览








文档简介
课件27张PPT。4.3 一次函数的图象?
第1课时1.能熟练作出正比例函数图象并熟记作图步骤.(重点)
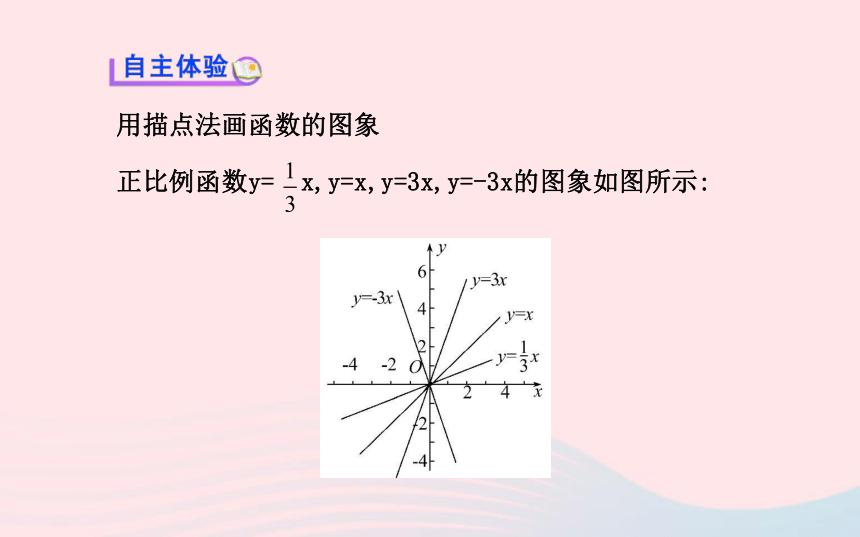
2.理解正比例函数及其图象的有关性质.(难点)用描点法画函数的图象
正比例函数y= x,y=x,y=3x,y=-3x的图象如图所示:【思考】
(1)图中的直线有公共交点吗?如果有,是什么?
提示:有公共交点,公共交点是原点.
(2)上面四个函数中,哪些函数的y的值随着x值的增大而增大?
哪些函数的y的值随着x值的增大而减小?
提示:函数y= x,y=x,y=3x的y的值随着x值的增大而增大,函数
y=-3x的y的值随着x值的增大而减小.【总结】
1.正比例函数的图象及性质:
(1)图象:一般地,直线y=kx(k为常数,k≠0)是一条_________的
直线.
(2)性质:①当k>0时,直线y=kx经过第_______象限,从左向右上
升,y随x的增大而_____.
②当k<0时,直线y=kx经过第_______象限,从左向右下降,y随x
的增大而_____.经过原点一、三增大二、四减小2.根据两点确定一条直线,画正比例函数的图象时,经过直线上
两点______和(1,__)画直线更简单.(0,0)k (打“√”或“×”)
(1)函数y= x的性质是y随x的增大而减小. ( )
(2)函数y=-3x的性质是y随x的增大而减小. ( )
(3)点(2,6)在函数y=3x的图象上. ( )
(4)直线y=-0.5x经过点(4,2). ( )×√√×知识点 1 正比例函数的图象?
【例1】在同一直角坐标系内画出正比例函数y=-2x与y=0.5x的
图象.
【解题探究】
(1)正比例函数的图象是_________.
(2)正比例函数y=kx的图象一定经过______和______两点.一条直线(0,0)(1,k)(3)由问题(1)(2)的探究,你能确定画正比例函数y=-2x与y=0.5x的图象的方法吗?
提示:经过(0,0)和(1,-2)两点即可作出y=-2x的图象,经过(0,0)和(1,0.5)两点即可作出y=0.5x的图象.
(4)请按照(3)中的方法画出这两个函数的图象.
提示:【互动探究】请你用量角器度量一下你所画的这两条直线所成的夹角,你会发现什么?写出你的猜想.
提示:两条直线所成的夹角为90°.当两个正比例函数的系数之积为-1时,两条直线互相垂直.【总结提升】由正比例函数的表达式画函数图象的三个步骤
1.列表:列表给出自变量x=1和x=0时对应的函数值.
2.描点:以表中对应值为坐标在直角坐标系中找出相应的点.
3.连线:过所描点作直线.知识点 2 正比例函数的性质
【例2】已知函数 当k为何值时,正比例函数y随
x的增大而减小?
【思路点拨】先根据正比例函数的定义可得k2-3=1,再由y随x
的增大而减小确定k的值.【自主解答】因为此函数是正比例函数,所以k2-3=1,
所以k=±2,
因为正比例函数y随x的增大而减小,
所以k-1<0,
因此k=2时,不合题意,
所以k=-2.【总结提升】 正比例函数的性质
对于正比例函数y=kx(k≠0),k的符号、图象所经过的象限、函数的增减性这三者,知其一则知其二,即:题组一:正比例函数的图象
1.当k>0时,正比例函数y=kx的图象大致是 ( )
【解析】选A.正比例函数的图象是一条经过原点的直线,且当k>0时,图象经过第一、三象限.2.若正比例函数y=kx的图象经过点(1,2),则k的值为 ( )
A.- B.-2 C. D.2
【解析】选D.∵正比例函数y=kx的图象经过点(1,2),∴k=2.3.若正比例函数y=kx的图象经过点(-1,2),则这个图象必经过点 ( )
A.(1,2) B.(-1,-2)
C.(2,-1) D.(1,-2)
【解析】选D.因为正比例函数y=kx的图象经过点(-1,2),所以2=-k,解得k=-2,所以y=-2x,把这四个选项中的点的坐标分别代入y=-2x中,等号成立的点就在正比例函数y=-2x的图象上,所以这个图象必经过点(1,-2).4.写出一个正比例函数,使其图象经过第二、四象限: .
【解析】设此正比例函数的表达式为y=kx(k≠0),∵此正比例函数的图象经过第二、四象限,∴k<0,∴符合条件的正比例函数的表达式可以为y=-x(答案不唯一).
答案:y=-x(答案不唯一)5.在同一直角坐标系中,画出函数y= x,y=x,y=5x的图象,然后
比较哪一个与x轴正方向所成的锐角最小,由此你得到什么猜想?
再选几个图象验证你的猜想.
【解析】如图所示:由以上三个函数的图象可知函数y= x与x轴正方向所成的锐角
最小,由此可知正比例函数y=kx(k>0)中,k越小图象与x轴正方
向所成的锐角越小.再画出函数y= x与函数y=2x的图象进行比
较也成立.题组二:正比例函数的性质
1.已知函数y=kx的函数值随x的增大而减小,则函数的图象经过
( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
【解析】选D.根据题意,函数值随x的增大而减小,k值小于0,图
象经过第二、四象限.2.已知正比例函数y=(3k-1)x,若y随x的增大而增大,则k的取值
范围是 ( )
A.k<0 B.k>0
C.k< D.k>
【解析】选D.根据y随x的增大而增大,知:3k-1>0,即k> .3.若正比例函数y=kx(k为常数,且k≠0)的函数值y随x的增大而减小,则k的值可以是 .(写出一个即可).
【解析】因为函数值y随x的增大而减小,所以k<0,所以k可以为-2,-1等.
答案:-1(不唯一,只要k<0即可)4.已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),
则y1 y2(填“>”或“<”或“=”).
【解析】方法一:把点A(-1,y1),点B(-2,y2)分别代入函数y=3x,求得y1=-3,y2=-6,所以y1>y2.方法二:如图,观察图形,显然得y1>y2.
方法三:根据正比例函数的性质,当k>0时,y随x值的增大而增大,也就是当k>0时,y随x值的减小而减小,即可得y1>y2.
答案:>5.若正比例函数 y随x的增大而增大,求m的值,
并写出该函数的表达式.
【解析】由题意得
解得m=1.当m=1时,y=3x.【想一想错在哪?】如果每千克白菜的价格为2元,请写出所需费用y(元)与所买白菜的质量x(千克)之间的关系,并画出图象.
提示:实际问题中的函数图象要注意自变量的取值范围,本题的函数图象应为射线.
第1课时1.能熟练作出正比例函数图象并熟记作图步骤.(重点)
2.理解正比例函数及其图象的有关性质.(难点)用描点法画函数的图象
正比例函数y= x,y=x,y=3x,y=-3x的图象如图所示:【思考】
(1)图中的直线有公共交点吗?如果有,是什么?
提示:有公共交点,公共交点是原点.
(2)上面四个函数中,哪些函数的y的值随着x值的增大而增大?
哪些函数的y的值随着x值的增大而减小?
提示:函数y= x,y=x,y=3x的y的值随着x值的增大而增大,函数
y=-3x的y的值随着x值的增大而减小.【总结】
1.正比例函数的图象及性质:
(1)图象:一般地,直线y=kx(k为常数,k≠0)是一条_________的
直线.
(2)性质:①当k>0时,直线y=kx经过第_______象限,从左向右上
升,y随x的增大而_____.
②当k<0时,直线y=kx经过第_______象限,从左向右下降,y随x
的增大而_____.经过原点一、三增大二、四减小2.根据两点确定一条直线,画正比例函数的图象时,经过直线上
两点______和(1,__)画直线更简单.(0,0)k (打“√”或“×”)
(1)函数y= x的性质是y随x的增大而减小. ( )
(2)函数y=-3x的性质是y随x的增大而减小. ( )
(3)点(2,6)在函数y=3x的图象上. ( )
(4)直线y=-0.5x经过点(4,2). ( )×√√×知识点 1 正比例函数的图象?
【例1】在同一直角坐标系内画出正比例函数y=-2x与y=0.5x的
图象.
【解题探究】
(1)正比例函数的图象是_________.
(2)正比例函数y=kx的图象一定经过______和______两点.一条直线(0,0)(1,k)(3)由问题(1)(2)的探究,你能确定画正比例函数y=-2x与y=0.5x的图象的方法吗?
提示:经过(0,0)和(1,-2)两点即可作出y=-2x的图象,经过(0,0)和(1,0.5)两点即可作出y=0.5x的图象.
(4)请按照(3)中的方法画出这两个函数的图象.
提示:【互动探究】请你用量角器度量一下你所画的这两条直线所成的夹角,你会发现什么?写出你的猜想.
提示:两条直线所成的夹角为90°.当两个正比例函数的系数之积为-1时,两条直线互相垂直.【总结提升】由正比例函数的表达式画函数图象的三个步骤
1.列表:列表给出自变量x=1和x=0时对应的函数值.
2.描点:以表中对应值为坐标在直角坐标系中找出相应的点.
3.连线:过所描点作直线.知识点 2 正比例函数的性质
【例2】已知函数 当k为何值时,正比例函数y随
x的增大而减小?
【思路点拨】先根据正比例函数的定义可得k2-3=1,再由y随x
的增大而减小确定k的值.【自主解答】因为此函数是正比例函数,所以k2-3=1,
所以k=±2,
因为正比例函数y随x的增大而减小,
所以k-1<0,
因此k=2时,不合题意,
所以k=-2.【总结提升】 正比例函数的性质
对于正比例函数y=kx(k≠0),k的符号、图象所经过的象限、函数的增减性这三者,知其一则知其二,即:题组一:正比例函数的图象
1.当k>0时,正比例函数y=kx的图象大致是 ( )
【解析】选A.正比例函数的图象是一条经过原点的直线,且当k>0时,图象经过第一、三象限.2.若正比例函数y=kx的图象经过点(1,2),则k的值为 ( )
A.- B.-2 C. D.2
【解析】选D.∵正比例函数y=kx的图象经过点(1,2),∴k=2.3.若正比例函数y=kx的图象经过点(-1,2),则这个图象必经过点 ( )
A.(1,2) B.(-1,-2)
C.(2,-1) D.(1,-2)
【解析】选D.因为正比例函数y=kx的图象经过点(-1,2),所以2=-k,解得k=-2,所以y=-2x,把这四个选项中的点的坐标分别代入y=-2x中,等号成立的点就在正比例函数y=-2x的图象上,所以这个图象必经过点(1,-2).4.写出一个正比例函数,使其图象经过第二、四象限: .
【解析】设此正比例函数的表达式为y=kx(k≠0),∵此正比例函数的图象经过第二、四象限,∴k<0,∴符合条件的正比例函数的表达式可以为y=-x(答案不唯一).
答案:y=-x(答案不唯一)5.在同一直角坐标系中,画出函数y= x,y=x,y=5x的图象,然后
比较哪一个与x轴正方向所成的锐角最小,由此你得到什么猜想?
再选几个图象验证你的猜想.
【解析】如图所示:由以上三个函数的图象可知函数y= x与x轴正方向所成的锐角
最小,由此可知正比例函数y=kx(k>0)中,k越小图象与x轴正方
向所成的锐角越小.再画出函数y= x与函数y=2x的图象进行比
较也成立.题组二:正比例函数的性质
1.已知函数y=kx的函数值随x的增大而减小,则函数的图象经过
( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
【解析】选D.根据题意,函数值随x的增大而减小,k值小于0,图
象经过第二、四象限.2.已知正比例函数y=(3k-1)x,若y随x的增大而增大,则k的取值
范围是 ( )
A.k<0 B.k>0
C.k< D.k>
【解析】选D.根据y随x的增大而增大,知:3k-1>0,即k> .3.若正比例函数y=kx(k为常数,且k≠0)的函数值y随x的增大而减小,则k的值可以是 .(写出一个即可).
【解析】因为函数值y随x的增大而减小,所以k<0,所以k可以为-2,-1等.
答案:-1(不唯一,只要k<0即可)4.已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),
则y1 y2(填“>”或“<”或“=”).
【解析】方法一:把点A(-1,y1),点B(-2,y2)分别代入函数y=3x,求得y1=-3,y2=-6,所以y1>y2.方法二:如图,观察图形,显然得y1>y2.
方法三:根据正比例函数的性质,当k>0时,y随x值的增大而增大,也就是当k>0时,y随x值的减小而减小,即可得y1>y2.
答案:>5.若正比例函数 y随x的增大而增大,求m的值,
并写出该函数的表达式.
【解析】由题意得
解得m=1.当m=1时,y=3x.【想一想错在哪?】如果每千克白菜的价格为2元,请写出所需费用y(元)与所买白菜的质量x(千克)之间的关系,并画出图象.
提示:实际问题中的函数图象要注意自变量的取值范围,本题的函数图象应为射线.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
