8.2 消元——解二元一次方程(第1课时)课件(共10张PPT)
文档属性
| 名称 | 8.2 消元——解二元一次方程(第1课时)课件(共10张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 76.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 18:16:32 | ||
图片预览




文档简介
课件10张PPT。
人教版 七年级数学下册
第8章 二元一次方程组
8.2 消元——解二元一次方程(第1课时)
学习目标:会用代入法解二元一次方程组。
学习重点:用代入法解二元一次方程组的一般步骤。
学习难点:体会代入消元思想、方程和方程组的思想
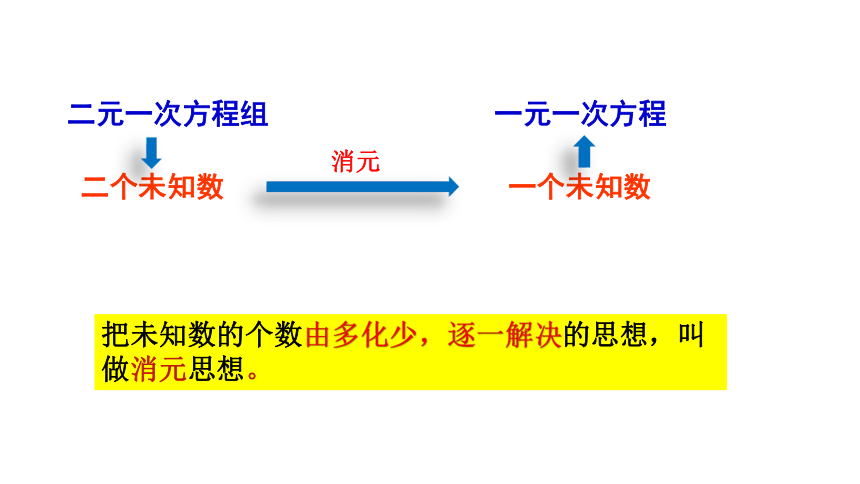
以及把未知转化为已知的转化思想。 二元一次方程组 把未知数的个数由多化少,逐一解决的思想,叫做消元思想。消元例1 解方程组解:由①得:x = 3+ y③把③代入②得:3(3+y)– 8y= 14把y= – 1代入①,得x = 22、用变形后的式子代入到另一个方程中,得到一个一元一次方程,求出一个未知数的值;3、把已求出的未知数的值代入原方程组的方程中,求出另一个未知数的值;4、写出方程组的解。变代求写9+3y– 8y= 14– 5y= 5y= – 1代入消元法:3 x – 8y = 14x = 3+y 3+y(3+y)分析1、将方程组里的一个方程变形,变为用含有一个未知数的式子表示另一个未知数的形式;练习:1.把下列式子变为用含x的式子表示y的形式。①x+y=3①-x+y=3③2(x+y)-3(x-y)=3②x+2y=-42.把x=-3-y 代入到下列各式之中,并求出y的解。②-2x-3y=3y=3-x-x+5y=32x+2y-3x+3y=32y=-4-x3(x+y)-2(y-x)=63x+3y-2y+2x=65x+y=6y=6-5x-(-3-y)+y=33+y+y=3y=0-2(-3-y)-3y=36+2y-3y=3y=3y=______________xx3.用代入法解下列二元一次方程组解:把②代入①得:2(3b+2)+b=186b+4+b=18b=2把b=2代入方程②,得:a=8解:由①得:y=2x-5把③代入②得:3x+4(2x-5)=23x+8x-20=2x=2把x=2代入方程①,得:y=-1③
4.用代入法巧解二元一次方程组解:把①代入②得:5x-2×8 =-1x=3把x=3代入①得:y=5解:由①得:把③代入②得:x=1把x=1代入①得:y=2③ 5 . 已知 是二元一次方程组
的解,则 a= ,b= 。 6.已知 (a+2b-5)2+|4a+b-6|=0, 求a和b的值.311、二元一次方程组代入消元法2、代入消元法的一般步骤:3、思想方法:转化思想、消元思想、
方程(组)思想.变代求写转化一元一次方程1.把下列方程改写成用含x的式子表示y的形式(2)3x+y-1=0(1)2x-y=32.用代入法解下列方程组
人教版 七年级数学下册
第8章 二元一次方程组
8.2 消元——解二元一次方程(第1课时)
学习目标:会用代入法解二元一次方程组。
学习重点:用代入法解二元一次方程组的一般步骤。
学习难点:体会代入消元思想、方程和方程组的思想
以及把未知转化为已知的转化思想。 二元一次方程组 把未知数的个数由多化少,逐一解决的思想,叫做消元思想。消元例1 解方程组解:由①得:x = 3+ y③把③代入②得:3(3+y)– 8y= 14把y= – 1代入①,得x = 22、用变形后的式子代入到另一个方程中,得到一个一元一次方程,求出一个未知数的值;3、把已求出的未知数的值代入原方程组的方程中,求出另一个未知数的值;4、写出方程组的解。变代求写9+3y– 8y= 14– 5y= 5y= – 1代入消元法:3 x – 8y = 14x = 3+y 3+y(3+y)分析1、将方程组里的一个方程变形,变为用含有一个未知数的式子表示另一个未知数的形式;练习:1.把下列式子变为用含x的式子表示y的形式。①x+y=3①-x+y=3③2(x+y)-3(x-y)=3②x+2y=-42.把x=-3-y 代入到下列各式之中,并求出y的解。②-2x-3y=3y=3-x-x+5y=32x+2y-3x+3y=32y=-4-x3(x+y)-2(y-x)=63x+3y-2y+2x=65x+y=6y=6-5x-(-3-y)+y=33+y+y=3y=0-2(-3-y)-3y=36+2y-3y=3y=3y=______________xx3.用代入法解下列二元一次方程组解:把②代入①得:2(3b+2)+b=186b+4+b=18b=2把b=2代入方程②,得:a=8解:由①得:y=2x-5把③代入②得:3x+4(2x-5)=23x+8x-20=2x=2把x=2代入方程①,得:y=-1③
4.用代入法巧解二元一次方程组解:把①代入②得:5x-2×8 =-1x=3把x=3代入①得:y=5解:由①得:把③代入②得:x=1把x=1代入①得:y=2③ 5 . 已知 是二元一次方程组
的解,则 a= ,b= 。 6.已知 (a+2b-5)2+|4a+b-6|=0, 求a和b的值.311、二元一次方程组代入消元法2、代入消元法的一般步骤:3、思想方法:转化思想、消元思想、
方程(组)思想.变代求写转化一元一次方程1.把下列方程改写成用含x的式子表示y的形式(2)3x+y-1=0(1)2x-y=32.用代入法解下列方程组
